1. 计算下面长方体的体积。
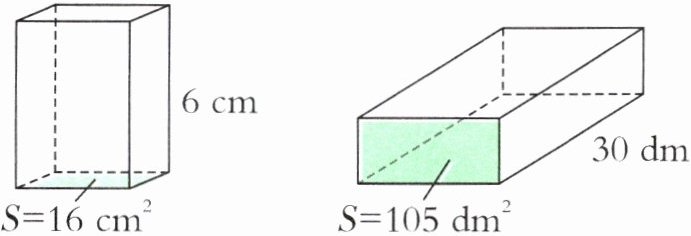

答案:16×6=96(cm³)
105×30=3150(dm³)
【提示】长方体的体积=底面积×高
105×30=3150(dm³)
【提示】长方体的体积=底面积×高
2. 传统文化 兵马俑坑 秦始皇陵兵马俑共有3个兵马俑坑,呈“品”字形排列。其中一号俑坑是长方体,东西长230米,南北宽62米,深约5米。一号俑坑的容积约是(
71300
)立方米。答案:71300 【提示】230×62×5=71300(立方米)
3. 如下图(单位:厘米),有一个完全封闭的容器,平放时里面的长是20厘米,宽是16厘米,高是10厘米,平放时里面装有7厘米深的水。如果把这个容器的前面作为底面竖起来放,那么水面的高度是(

A.11.2
B.11
C.16
D.14
A
)厘米。
A.11.2
B.11
C.16
D.14
答案:A 【提示】两种放法里面的水的体积不变,所以水面高20×16×7÷(20×10)=11.2(厘米)。
4. 一根长方体木料长1.5米,把它截成3个小长方体后(如下图),表面积比原来增加了0.64平方米。原来这根木料的体积是多少立方米?


答案:0.64÷(2×2)=0.16(平方米)
0.16×1.5=0.24(立方米)
【提示】截成3段一共增加了2×2=4(个)横截面,所以1个横截面的面积是(0.64÷4)平方米,用1个横截面的面积乘原来木料的长度就可以求出原来这根木料的体积。
0.16×1.5=0.24(立方米)
【提示】截成3段一共增加了2×2=4(个)横截面,所以1个横截面的面积是(0.64÷4)平方米,用1个横截面的面积乘原来木料的长度就可以求出原来这根木料的体积。
5. 新考法 条件选择 四名同学观察并测量了一个长方体。
丁丁说:“如果高减少2分米,它恰好是一个正方体。”
当当说:“长方体的前、后、左、右四个面的面积之和是192平方分米。”
玲玲说:“它的底面是正方形,周长是24分米。”
冬冬说:“这个长方体的棱长总和是80分米。”
四人得到的数据都是正确的,请筛选出必要的数据作为条件,求出这个长方体的体积。
丁丁说:“如果高减少2分米,它恰好是一个正方体。”
当当说:“长方体的前、后、左、右四个面的面积之和是192平方分米。”
玲玲说:“它的底面是正方形,周长是24分米。”
冬冬说:“这个长方体的棱长总和是80分米。”
四人得到的数据都是正确的,请筛选出必要的数据作为条件,求出这个长方体的体积。
答案:选法不唯一,如:选当当和玲玲所说的数据。
192÷4×(24÷4)=288(立方分米)
【提示】这个长方体的底面是正方形,则它的前、后、左、右四个面的面积相等,因此其中一个面的面积是192÷4=48(平方分米),这个面对应的高是24÷4=6(分米),根据“长方体的体积=底面积×高”即可求出答案。
192÷4×(24÷4)=288(立方分米)
【提示】这个长方体的底面是正方形,则它的前、后、左、右四个面的面积相等,因此其中一个面的面积是192÷4=48(平方分米),这个面对应的高是24÷4=6(分米),根据“长方体的体积=底面积×高”即可求出答案。
6. 新考法 评价说明 一个长6厘米、宽4厘米、高5厘米的长方体盒子中(盒子的厚度忽略不计),最多能放多少个棱长为2厘米的正方体?
下面是小虎的做法:
(6×4×5)÷(2×2×2)= 15(个)
答:最多能放15个棱长为2厘米的正方体。
(1)小虎的做法错在哪里?
(2)请你把正确的做法写在下面。
下面是小虎的做法:
(6×4×5)÷(2×2×2)= 15(个)
答:最多能放15个棱长为2厘米的正方体。
(1)小虎的做法错在哪里?
(2)请你把正确的做法写在下面。
答案:
(1)小虎的做法错在未考虑空间适配,长方体盒子竖着只能摆2层,余下的空间摆不下棱长2厘米的正方体了。
(2)6÷2=3(个) 5÷2=2(个)……1(厘米)
4÷2=2(个) 3×2×2=12(个)
【提示】本题需先求出沿着长方体盒子的长、宽、高分别可以摆几个正方体,再相乘即可求解。
(1)小虎的做法错在未考虑空间适配,长方体盒子竖着只能摆2层,余下的空间摆不下棱长2厘米的正方体了。
(2)6÷2=3(个) 5÷2=2(个)……1(厘米)
4÷2=2(个) 3×2×2=12(个)
【提示】本题需先求出沿着长方体盒子的长、宽、高分别可以摆几个正方体,再相乘即可求解。