(1)小红在超市购买了3包饼干和2盒果冻,一共花了22.5元。已知每包饼干比每盒果冻便宜2.5元,则每包饼干(
3.5
)元。若购买2包饼干和3盒果冻,则一共需要(25
)元。答案:
(1)3.5 25
(1)3.5 25
解析:
设每盒果冻$x$元,则每包饼干$(x - 2.5)$元。
$3(x - 2.5) + 2x = 22.5$
$3x - 7.5 + 2x = 22.5$
$5x = 30$
$x = 6$
每包饼干:$6 - 2.5 = 3.5$(元)
购买2包饼干和3盒果冻需要:$2×3.5 + 3×6 = 7 + 18 = 25$(元)
3.5 25
$3(x - 2.5) + 2x = 22.5$
$3x - 7.5 + 2x = 22.5$
$5x = 30$
$x = 6$
每包饼干:$6 - 2.5 = 3.5$(元)
购买2包饼干和3盒果冻需要:$2×3.5 + 3×6 = 7 + 18 = 25$(元)
3.5 25
(2)“六一”儿童节,同学们用红、黄、蓝三种颜色的气球共144个布置会场,已知黄气球比红气球多4个,蓝气球比黄气球多28个,则红气球有(
36
)个,黄气球有(40
)个,蓝气球有(68
)个。答案:
(2)36 40 68
(2)36 40 68
解析:
设红气球有$x$个,则黄气球有$x + 4$个,蓝气球有$(x + 4) + 28 = x + 32$个。
根据题意可得方程:$x + (x + 4) + (x + 32) = 144$
化简得:$3x + 36 = 144$
移项得:$3x = 144 - 36$
计算得:$3x = 108$
解得:$x = 36$
黄气球:$36 + 4 = 40$(个)
蓝气球:$40 + 28 = 68$(个)
36 40 68
根据题意可得方程:$x + (x + 4) + (x + 32) = 144$
化简得:$3x + 36 = 144$
移项得:$3x = 144 - 36$
计算得:$3x = 108$
解得:$x = 36$
黄气球:$36 + 4 = 40$(个)
蓝气球:$40 + 28 = 68$(个)
36 40 68
2. 一份数学试卷有25题,答对1题得4分,答错或不答倒扣1分。小明得了60分,他答对了(
A.16题
B.17题
C.18题
B
)。A.16题
B.17题
C.18题
答案:B
解析:
设小明答对了$x$题,则答错或不答$(25 - x)$题。
$4x - 1×(25 - x) = 60$
$4x - 25 + x = 60$
$5x = 85$
$x = 17$
B
$4x - 1×(25 - x) = 60$
$4x - 25 + x = 60$
$5x = 85$
$x = 17$
B
3. 新情境 世界环境日 6月5日是世界环境日,我国2025年的主题是“美丽中国我先行”。六(1)班49名学生举行“减少白色污染”宣传活动,有5人组和3人组两种分组方法,正好组成了11个小组,5人组和3人组各有几组?
答案:3人组:(5×11-49)÷(5-3)=3(组) 5人组:11-3=8(组)
解析:
3人组:$(5×11 - 49)÷(5 - 3)=3$(组)
5人组:$11 - 3=8$(组)
5人组:$11 - 3=8$(组)
4. 新考法 图形规律探究 准备若干个棱长为1厘米的正方体,将正方体一个接一个拼接起来,并将拼成的立体图形的表面积写在右侧横线上。观察正方体的个数与所拼成的立体图形的表面积之间有什么关系?
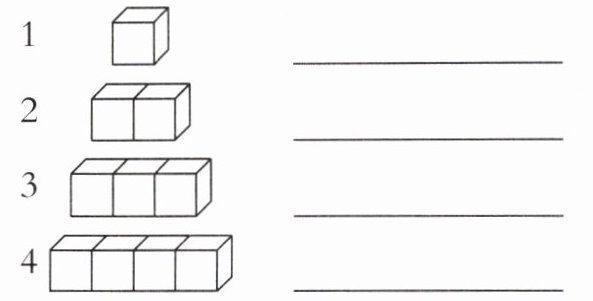
发现:
推想:当正方体的个数是10时,所拼成的立体图形的表面积是(

发现:
每增加一个正方体,表面积就增加4个正方形面的面积
推想:当正方体的个数是10时,所拼成的立体图形的表面积是(
42
)平方厘米。当正方体的个数是n时,所拼成的立体图形的表面积是(4n+2
)平方厘米。答案:6平方厘米 10平方厘米 14平方厘米 18平方厘米 发现:每增加一个正方体,表面积就增加4个正方形面的面积。 推想:当正方体的个数是10时,所拼成的立体图形的表面积是
(42)平方厘米。当正方体的个数是n时,所拼成的立体图形的表面积是(4n+2)平方厘米。【提示】可以通过数一数前几行的正方形数量来得到立体图形的面积,这个过程中不难发现,每次增加一个正方体,表面积就增加4平方厘米。因此,有n个正方体时,图形的表面积是(4n+2)平方厘米。
(42)平方厘米。当正方体的个数是n时,所拼成的立体图形的表面积是(4n+2)平方厘米。【提示】可以通过数一数前几行的正方形数量来得到立体图形的面积,这个过程中不难发现,每次增加一个正方体,表面积就增加4平方厘米。因此,有n个正方体时,图形的表面积是(4n+2)平方厘米。
5. 实验班原创 应用意识 学校要为六年级毕业典礼印制节目单,按市场价格,制版费900元,印制每份节目单的价格为1.5元。现在有两个印刷厂可供选择,优惠方式如下:
甲印刷厂:制版费不优惠,每份节目单八折优惠。
乙印刷厂:制版费六折优惠,每份节目单不优惠。
(1)如果学校要印制1000份节目单,那么选择(
(2)如果学校要印制1500份节目单,那么选择(
(3)印制多少份时,甲印刷厂和乙印刷厂所需要的费用一样?
甲印刷厂:制版费不优惠,每份节目单八折优惠。
乙印刷厂:制版费六折优惠,每份节目单不优惠。
(1)如果学校要印制1000份节目单,那么选择(
乙
)印刷厂费用少。(2)如果学校要印制1500份节目单,那么选择(
甲
)印刷厂费用少。(3)印制多少份时,甲印刷厂和乙印刷厂所需要的费用一样?
方法一:(900-900×0.6)÷(1.5-1.5×0.8)=1200(份) 方法二:设印制x份时,两印刷厂需要的费用一样。900+1.5×0.8x=900×0.6+1.5x x=1200 印刷1200份时,两印刷厂需要的费用一样。
答案:
(1)乙
(2)甲
(3)方法一:(900-900×0.6)÷(1.5-1.5×0.8)=1200(份) 方法二:设印制x份时,两印刷厂需要的费用一样。900+1.5×0.8x=900×0.6+1.5x x=1200 印刷1200份时,两印刷厂需要的费用一样。
(1)乙
(2)甲
(3)方法一:(900-900×0.6)÷(1.5-1.5×0.8)=1200(份) 方法二:设印制x份时,两印刷厂需要的费用一样。900+1.5×0.8x=900×0.6+1.5x x=1200 印刷1200份时,两印刷厂需要的费用一样。