1. 求下面图形的表面积和体积。(单位:cm)
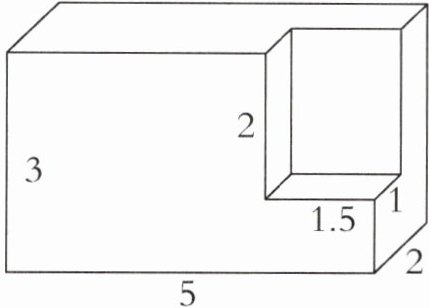

答案:(5×3+5×2+3×2)×2=62(cm²)
5×2×3 - 1.5×1×2=27(cm³)
[提示]这个立体图形的表面积等于长5cm、宽2cm、高3cm的长方体的表面积,体积等于大长方体的体积减去小长方体的体积。
5×2×3 - 1.5×1×2=27(cm³)
[提示]这个立体图形的表面积等于长5cm、宽2cm、高3cm的长方体的表面积,体积等于大长方体的体积减去小长方体的体积。
(1)在括号里填合适的数。
$\frac{3}{8}$立方米= (
360毫升= (
$\frac{3}{8}$立方米= (
375
)立方分米360毫升= (
0.36
)升答案:
(1)375 0.36
(1)375 0.36
解析:
$\frac{3}{8}$立方米$=375$立方分米
360毫升$=0.36$升
360毫升$=0.36$升
(2)把一个长4分米、宽2分米、高2分米的长方体切成两个小正方体,表面积增加了
8
平方分米,每个小正方体的体积是8
立方分米。答案:
(2)8 8
(2)8 8
解析:
表面积增加:$2×2×2 = 8$(平方分米)
每个小正方体体积:$2×2×2 = 8$(立方分米)
8;8
每个小正方体体积:$2×2×2 = 8$(立方分米)
8;8
(3)把一个正方体的六个面都涂上颜色,切成27块大小相同的小正方体(如右图)。

①一面涂色的小正方体有(
②两面涂色的小正方体有(
③三面涂色的小正方体有(

①一面涂色的小正方体有(
6
)块。②两面涂色的小正方体有(
12
)块。③三面涂色的小正方体有(
8
)块。答案:
(3)①6 ②12 ③8
(3)①6 ②12 ③8
解析:
①6
②12
③8
②12
③8
3. 如右图,一只蚂蚁要从点M爬到点N,若只允许沿着三条棱爬行且不绕行,则一共有( )条路线。

A.4
B.6
C.8
D.9

A.4
B.6
C.8
D.9
答案:
B [提示]如下图,路线一:M→D→A→N;路线二:M→B→A→N;路线三:M→D→E→N;路线四:M→F→E→N;路线五:M→B→C→N;路线六:M→F→C→N。共6条。
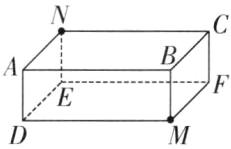
B [提示]如下图,路线一:M→D→A→N;路线二:M→B→A→N;路线三:M→D→E→N;路线四:M→F→E→N;路线五:M→B→C→N;路线六:M→F→C→N。共6条。

4. 一个密封的玻璃缸(如图①),从里面量长9分米,宽5分米,高6分米,现在玻璃缸里的水深为5分米。

(1)这个密封的玻璃缸里装了多少升水?
(2)如果将玻璃缸竖起来放(如图②),那么缸里水深多少分米?

(1)这个密封的玻璃缸里装了多少升水?
(2)如果将玻璃缸竖起来放(如图②),那么缸里水深多少分米?
答案:
(1)9×5×5=225(立方分米)
225立方分米=225升
(2)225÷(5×6)=7.5(分米)
(1)9×5×5=225(立方分米)
225立方分米=225升
(2)225÷(5×6)=7.5(分米)
5. 有一个两层水箱,如下图所示。(单位:分米)

(1)第二层水箱容积是多少升?
(2)如果注满第一层需要7.5分钟,照这样的流速,注满整个水箱需要多少分钟?

(1)第二层水箱容积是多少升?
(2)如果注满第一层需要7.5分钟,照这样的流速,注满整个水箱需要多少分钟?
答案:
(1)(6+2+2)×5×2=100(立方分米)
100立方分米=100升
(2)第一层水箱容积:6×5×2=60(立方分米)
60立方分米=60升
100÷(60÷7.5)+7.5=20(分钟)
[提示]
(1)观察图形可以发现,第二层水箱的长比第一层的多4分米,便可以用长方体的体积公式求出第二层水箱的容积。
(2)用第一层水箱的容积除以时间,就能算出流速,进而能求出注满整个水箱的时间。
(1)(6+2+2)×5×2=100(立方分米)
100立方分米=100升
(2)第一层水箱容积:6×5×2=60(立方分米)
60立方分米=60升
100÷(60÷7.5)+7.5=20(分钟)
[提示]
(1)观察图形可以发现,第二层水箱的长比第一层的多4分米,便可以用长方体的体积公式求出第二层水箱的容积。
(2)用第一层水箱的容积除以时间,就能算出流速,进而能求出注满整个水箱的时间。