3. (
48
)千克的$\frac{3}{4}$是36千克;6元比4.8元多(25
)\%。答案:48 25
解析:
36÷$\frac{3}{4}$=48
(6-4.8)÷4.8×100%=25%
48 25
(6-4.8)÷4.8×100%=25%
48 25
4. 小亮周末步行去新华书店买书,$\frac{3}{5}小时走了\frac{5}{2}$千米,小亮步行的路程与时间的最简整数比是
25:6
,比值是$\frac{25}{6}$
。答案:$25:6$ $\frac{25}{6}$
解析:
路程与时间的比为$\frac{5}{2}:\frac{3}{5}$,化简得$(\frac{5}{2}×10):(\frac{3}{5}×10)=25:6$,比值是$\frac{25}{6}$。
25:6;$\frac{25}{6}$
25:6;$\frac{25}{6}$
5. 一堆黄沙重$\frac{16}{3}$吨,用去了$\frac{1}{8}$,还剩总数的$\frac{
7
}{8
}$,再用去$\frac{1}{8}$吨,这时还剩$$\frac{109}{24}$
$吨。答案:$\frac{7}{8}$ $\frac{109}{24}$
6. 六(1)班有男生24人,女生26人。男生人数占全班人数的
48
%;这天有两人因病休息,这天六(1)班的出席率为96
%。答案:48 96
解析:
全班人数:$24 + 26 = 50$(人)
男生人数占全班人数的百分比:$\frac{24}{50} × 100\% = 48\%$
出席人数:$50 - 2 = 48$(人)
出席率:$\frac{48}{50} × 100\% = 96\%$
48 96
男生人数占全班人数的百分比:$\frac{24}{50} × 100\% = 48\%$
出席人数:$50 - 2 = 48$(人)
出席率:$\frac{48}{50} × 100\% = 96\%$
48 96
7. $\frac{5}{4}千克花生可榨花生油\frac{3}{4}$升,平均每千克花生榨油
$\frac{3}{5}$
升,3
千克花生可榨$\frac{9}{5}$升花生油。答案:$\frac{3}{5}$ 3
解析:
$\frac{3}{4} ÷ \frac{5}{4} = \frac{3}{5}$(升)
$\frac{9}{5} ÷ \frac{3}{5} = 3$(千克)
$\frac{3}{5}$ 3
$\frac{9}{5} ÷ \frac{3}{5} = 3$(千克)
$\frac{3}{5}$ 3
8. 张老师得到了8000元稿费,他把钱存入银行,定期两年,年利率是$1.5\%$。到期后,张老师一共可以拿到
8240
元。答案:8240
解析:
利息:$8000×1.5\%×2 = 240$(元)
到期后一共可以拿到:$8000 + 240 = 8240$(元)
8240
到期后一共可以拿到:$8000 + 240 = 8240$(元)
8240
9. 丁丁在某一购票APP上按八折的优惠价购买了2张电影票,一共用去了64元,每张电影票的原价是
40
元。另一个购物软件上的优惠活动是按原价的$75\%$出售,广告语可以设计为“买三
送一”。答案:40 三
解析:
设每张电影票的原价是$x$元。
$2×0.8x = 64$
$1.6x=64$
$x=40$
设“买$n$送一”,则$(n + 1)$张票的现价等于$n$张票的原价。
$n×40=(n + 1)×40×75\%$
$n=(n + 1)×0.75$
$n=0.75n + 0.75$
$0.25n=0.75$
$n = 3$
40 三
$2×0.8x = 64$
$1.6x=64$
$x=40$
设“买$n$送一”,则$(n + 1)$张票的现价等于$n$张票的原价。
$n×40=(n + 1)×40×75\%$
$n=(n + 1)×0.75$
$n=0.75n + 0.75$
$0.25n=0.75$
$n = 3$
40 三
10. 思思看一本108页的科普书,第一天看了全书的$\frac{7}{18}$,第二天看的页数与第一天看的页数的比是$4:7$,第二天看了(
24
)页,她第三天应该从第(67
)页看起。答案:24 67
解析:
第一天看的页数:$108×\frac{7}{18}=42$(页)
第二天看的页数:$42×\frac{4}{7}=24$(页)
两天共看的页数:$42 + 24 = 66$(页)
第三天开始看的页数:$66 + 1 = 67$(页)
24 67
第二天看的页数:$42×\frac{4}{7}=24$(页)
两天共看的页数:$42 + 24 = 66$(页)
第三天开始看的页数:$66 + 1 = 67$(页)
24 67
11. 一个长方体木块,高减少4厘米后,就变成了一个正方体,这时表面积比原来少了80平方厘米,原来这个长方体木块的体积是
225
立方厘米。答案:225
解析:
设正方体的棱长为$x$厘米,则原长方体的长和宽均为$x$厘米,高为$(x + 4)$厘米。
高减少4厘米后,表面积减少的部分为4个相同的长方形的面积之和,每个长方形的长为$x$厘米,宽为4厘米。
根据题意可得:$4× x×4 = 80$
$16x = 80$
$x = 5$
原长方体的高为:$5 + 4 = 9$(厘米)
原长方体的体积为:$5×5×9 = 225$(立方厘米)
225
高减少4厘米后,表面积减少的部分为4个相同的长方形的面积之和,每个长方形的长为$x$厘米,宽为4厘米。
根据题意可得:$4× x×4 = 80$
$16x = 80$
$x = 5$
原长方体的高为:$5 + 4 = 9$(厘米)
原长方体的体积为:$5×5×9 = 225$(立方厘米)
225
12. 如右图,桌上有一张梯形纸片,折叠后,得到图形所覆盖桌面的面积是原来梯形面积的$\frac{3}{5}$,已知涂色部分的面积是4平方厘米,原来梯形的面积是$(
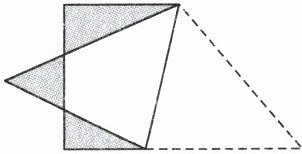
20
)$平方厘米。
答案:20
解析:
设原来梯形的面积是$S$平方厘米。
折叠后图形覆盖桌面的面积是$\frac{3}{5}S$,折叠部分(重合部分)的面积为$S - \frac{3}{5}S=\frac{2}{5}S$。
涂色部分面积 = 覆盖面积 - 重合部分面积,即$4=\frac{3}{5}S - \frac{2}{5}S$,$4=\frac{1}{5}S$,解得$S = 20$。
20
折叠后图形覆盖桌面的面积是$\frac{3}{5}S$,折叠部分(重合部分)的面积为$S - \frac{3}{5}S=\frac{2}{5}S$。
涂色部分面积 = 覆盖面积 - 重合部分面积,即$4=\frac{3}{5}S - \frac{2}{5}S$,$4=\frac{1}{5}S$,解得$S = 20$。
20
1. 一个尺寸为$506×620×1280(mm)$的物体,它最可能是(
A.一台冰箱
B.一台微波炉
C.一台笔记本电脑
D.一部手机
A
)。A.一台冰箱
B.一台微波炉
C.一台笔记本电脑
D.一部手机
答案:A
2. 如果$a和b$互为倒数,那么$\frac{a}{8}÷\frac{9}{b}= (
A.$\frac{a}{72}$
B.$\frac{1}{72}$
C.$\frac{b}{72}$
D.72
B
)$。A.$\frac{a}{72}$
B.$\frac{1}{72}$
C.$\frac{b}{72}$
D.72
答案:B
解析:
因为$a$和$b$互为倒数,所以$ab = 1$。
$\frac{a}{8}÷\frac{9}{b}=\frac{a}{8}×\frac{b}{9}=\frac{ab}{72}=\frac{1}{72}$
B
$\frac{a}{8}÷\frac{9}{b}=\frac{a}{8}×\frac{b}{9}=\frac{ab}{72}=\frac{1}{72}$
B
3. 给右图再加一个正方形,使它能折成一个正方体,有$(

A.2
B.3
C.4
D.5
C
)$种不同的方法。
A.2
B.3
C.4
D.5
答案:C
解析:
根据正方体展开图的特征,原图形已有5个正方形,需添加1个使其成为“1-4-1”“2-3-1”“2-2-2”“3-3”型中的一种。原图形可看作“3-2”结构(底层3个,上层2个),在不同位置添加正方形的情况如下:
1. 底层最左侧正方形的上方;
2. 底层最右侧正方形的上方;
3. 上层左侧正方形的左侧;
4. 上层右侧正方形的右侧。
共4种不同方法。
C
1. 底层最左侧正方形的上方;
2. 底层最右侧正方形的上方;
3. 上层左侧正方形的左侧;
4. 上层右侧正方形的右侧。
共4种不同方法。
C
4. 一个等腰三角形的周长是140厘米,其中两条边的长度比为$3:1$,底边的长是
A.35
B.20
C.84
D.20或84
B
厘米。A.35
B.20
C.84
D.20或84
答案:B
解析:
情况一:腰:底=3:1
设腰长为$3x$厘米,底边长为$x$厘米。
$3x + 3x + x = 140$
$7x = 140$
$x = 20$
腰长$3x = 60$厘米,底边长$20$厘米。
$60 + 20 > 60$,$60 + 60 > 20$,符合三角形三边关系。
情况二:底:腰=3:1
设底边长为$3x$厘米,腰长为$x$厘米。
$3x + x + x = 140$
$5x = 140$
$x = 28$
底边长$3x = 84$厘米,腰长$28$厘米。
$28 + 28 = 56 < 84$,不符合三角形三边关系,舍去。
底边的长是20厘米。
B
设腰长为$3x$厘米,底边长为$x$厘米。
$3x + 3x + x = 140$
$7x = 140$
$x = 20$
腰长$3x = 60$厘米,底边长$20$厘米。
$60 + 20 > 60$,$60 + 60 > 20$,符合三角形三边关系。
情况二:底:腰=3:1
设底边长为$3x$厘米,腰长为$x$厘米。
$3x + x + x = 140$
$5x = 140$
$x = 28$
底边长$3x = 84$厘米,腰长$28$厘米。
$28 + 28 = 56 < 84$,不符合三角形三边关系,舍去。
底边的长是20厘米。
B