8. 亮点原创 斑马线通常是由多条相互平行的白实线组成,好似斑马身上的线条,所以称作“斑马线”.A,B,C,D四位同学准备从斑马线上的点P处过马路,四人所走路线如图所示.假设四人速度相同,则最先通过马路的是
B
(填“A”“B”“C”或“D”),理由是垂线段最短
.答案：【解析】：
本题考查垂线段最短这一知识点。
从点P过马路，也就是从点P向对面马路边作线段。
在连接直线外一点与直线上各点的线段中，垂线段最短。
在这四位同学A、B、C、D中，B同学所走的路线是垂线段。
根据垂线段最短的性质，在速度相同的情况下，路程越短，所用时间越少，所以B同学最先通过马路。
【答案】：
B；垂线段最短
本题考查垂线段最短这一知识点。
从点P过马路，也就是从点P向对面马路边作线段。
在连接直线外一点与直线上各点的线段中，垂线段最短。
在这四位同学A、B、C、D中，B同学所走的路线是垂线段。
根据垂线段最短的性质，在速度相同的情况下，路程越短，所用时间越少，所以B同学最先通过马路。
【答案】：
B；垂线段最短
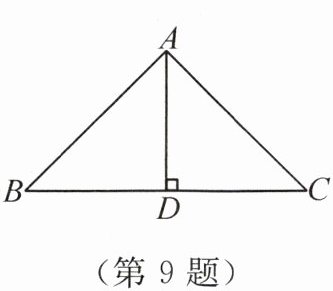
9. 如图,$∠BAC= 90^{\circ },AD⊥BC$,垂足为D,给出下列结论:① 点A到直线BC的距离是线段AD的长;② 线段AB的长是点B到直线AC的距离;③ 点C到直线AB的垂线段是线段AB.其中正确的是____.(填序号)
]
]
①②
答案：【解析】：本题可根据点到直线的距离的定义来逐一判断每个结论的正确性。
点到直线的距离的定义为：从直线外一点到这条直线所作的垂线段最短，这条垂线段的长度叫做这点到直线的距离。
判断结论①：点$A$到直线$BC$的距离是线段$AD$的长
已知$AD\perp BC$，垂足为$D$，即$AD$是从点$A$向直线$BC$所作的垂线段。
根据点到直线的距离的定义，从点$A$到直线$BC$的垂线段就是$AD$，所以点$A$到直线$BC$的距离是线段$AD$的长，该结论正确。
判断结论②：线段$AB$的长是点$B$到直线$AC$的距离
因为$\angle BAC = 90^{\circ}$，即$AB\perp AC$，$AB$是从点$B$向直线$AC$所作的垂线段。
根据点到直线的距离的定义，点$B$到直线$AC$的距离就是垂线段$AB$的长度，所以线段$AB$的长是点$B$到直线$AC$的距离，该结论正确。
判断结论③：点$C$到直线$AB$的垂线段是线段$AB$
由于$\angle BAC = 90^{\circ}$，即$AB\perp AC$，那么点$C$到直线$AB$的垂线段应该是$AC$，而不是$AB$，所以该结论错误。
综上，正确的结论是①②。
【答案】：①②
点到直线的距离的定义为：从直线外一点到这条直线所作的垂线段最短，这条垂线段的长度叫做这点到直线的距离。
判断结论①：点$A$到直线$BC$的距离是线段$AD$的长
已知$AD\perp BC$，垂足为$D$，即$AD$是从点$A$向直线$BC$所作的垂线段。
根据点到直线的距离的定义，从点$A$到直线$BC$的垂线段就是$AD$，所以点$A$到直线$BC$的距离是线段$AD$的长，该结论正确。
判断结论②：线段$AB$的长是点$B$到直线$AC$的距离
因为$\angle BAC = 90^{\circ}$，即$AB\perp AC$，$AB$是从点$B$向直线$AC$所作的垂线段。
根据点到直线的距离的定义，点$B$到直线$AC$的距离就是垂线段$AB$的长度，所以线段$AB$的长是点$B$到直线$AC$的距离，该结论正确。
判断结论③：点$C$到直线$AB$的垂线段是线段$AB$
由于$\angle BAC = 90^{\circ}$，即$AB\perp AC$，那么点$C$到直线$AB$的垂线段应该是$AC$，而不是$AB$，所以该结论错误。
综上，正确的结论是①②。
【答案】：①②
10. 如图,P,Q两点分别代表两个村庄,直线l代表这两个村庄之间的一条公路,根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1) 若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的公交站,请在公路l上画出公交站的位置(用点M表示),依据是
(2) 若考虑到修路的费用问题,希望公交站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出公交站的位置(用点N表示),依据是
]
(1) 若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的公交站,请在公路l上画出公交站的位置(用点M表示),依据是
垂线段最短
;(2) 若考虑到修路的费用问题,希望公交站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出公交站的位置(用点N表示),依据是
两点之间线段最短
.]
答案：【解析】：
本题主要考查了垂线段的性质以及两点之间线段最短的性质。
（1） 对于第一个问题，需要找到公路$l$上离村庄$P$最近的点$M$。根据垂线段的性质，从一点到直线的所有连线中，垂线段是最短的。因此，需要过点$P$作公路$l$的垂线，垂足即为所求的点$M$。
（2）对于第二个问题，需要找到公路$l$上到村庄$P$和村庄$Q$的距离之和最小的点$N$。根据两点之间线段最短的性质，可以直接连接点$P$和点$Q$，连线与公路$l$的交点即为所求的点$N$。这是因为线段$PQ$是点$P$和点$Q$之间的最短连线，而点$N$作为线段$PQ$与公路$l$的交点，自然满足到点$P$和点$Q$的距离之和最小。
【答案】：
（1）点$M$为所求；依据：垂线段最短。
（2） 点$N$为所求；依据：两点之间线段最短。
本题主要考查了垂线段的性质以及两点之间线段最短的性质。
（1） 对于第一个问题，需要找到公路$l$上离村庄$P$最近的点$M$。根据垂线段的性质，从一点到直线的所有连线中，垂线段是最短的。因此，需要过点$P$作公路$l$的垂线，垂足即为所求的点$M$。
（2）对于第二个问题，需要找到公路$l$上到村庄$P$和村庄$Q$的距离之和最小的点$N$。根据两点之间线段最短的性质，可以直接连接点$P$和点$Q$，连线与公路$l$的交点即为所求的点$N$。这是因为线段$PQ$是点$P$和点$Q$之间的最短连线，而点$N$作为线段$PQ$与公路$l$的交点，自然满足到点$P$和点$Q$的距离之和最小。
【答案】：
（1）点$M$为所求；依据：垂线段最短。
（2） 点$N$为所求；依据：两点之间线段最短。
11. 新素养 应用意识 如图,河道l的一侧有A,B两个村庄,现要铺设一条引水管道把河水引向A,B两个村庄.下列四种方案中,最节省材料的是 (
C
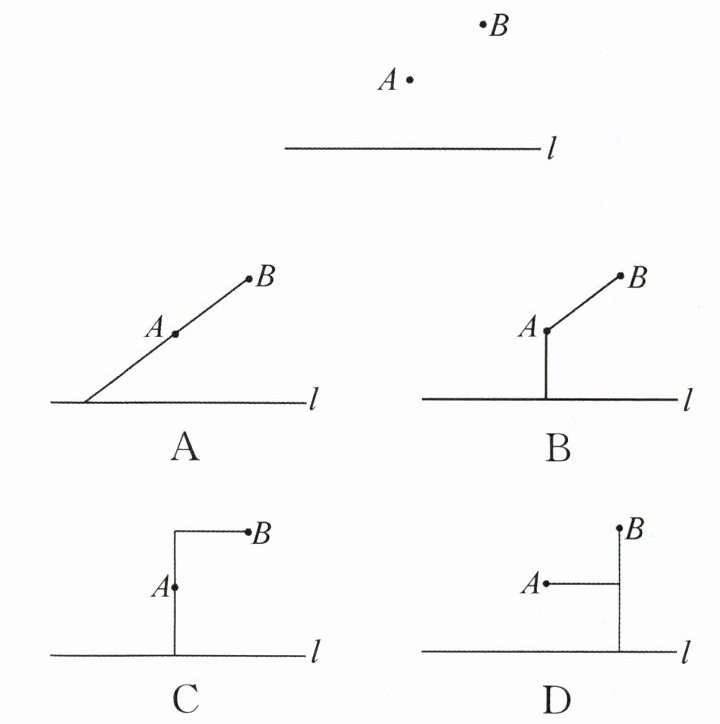
)答案：解：根据垂线段最短的性质，从直线外一点到这条直线所作的垂线段最短。要节省材料，需使引水管道总长度最短。观察各选项，方案C中从村庄A向河道l作垂线段，再连接A、B，此时管道总长度为垂线段长加AB长；方案D中从村庄B向河道l作垂线段，再连接A、B，管道总长度为垂线段长加AB长。由于A、B在河道同侧，比较A、B到河道l的距离，A离河道更近，方案C中垂线段更短，所以总长度更短。
答案：C
答案：C
12. (2025·江苏南京期末)如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1) 不考虑其他因素,请你画图确定蓄水池的位置,使它到这四个村庄的距离之和最小;
(2) 在(1)的条件下,计划把河水引入蓄水池中,怎样开渠最短? 画图并说明理由.
]
(1) 不考虑其他因素,请你画图确定蓄水池的位置,使它到这四个村庄的距离之和最小;
(2) 在(1)的条件下,计划把河水引入蓄水池中,怎样开渠最短? 画图并说明理由.
]
答案：(1) 解：连接AC、BD，两线段交于点P，点P即为所求蓄水池位置。
(2) 解：过点P作PH⊥EF于点H，沿PH开渠最短。理由：垂线段最短。
(2) 解：过点P作PH⊥EF于点H，沿PH开渠最短。理由：垂线段最短。