1. 如图,点C到直线l的距离为 (
A.线段CA的长
B.线段CB的长
C.线段CD的长
D.线段CM的长
]
C
)A.线段CA的长
B.线段CB的长
C.线段CD的长
D.线段CM的长
]
答案:【解析】:
本题考查了点到直线的距离的定义,即点到直线的垂线段的长度。
根据定义,点$C$到直线$l$的距离应该是从点$C$垂直落到直线$l$上的线段的长度。
观察图形,可以看到点$C$通过线段$CD$垂直落到直线$l$上,因此线段$CD$的长度就是点$C$到直线$l$的距离。
【答案】:C.线段$CD$的长。
本题考查了点到直线的距离的定义,即点到直线的垂线段的长度。
根据定义,点$C$到直线$l$的距离应该是从点$C$垂直落到直线$l$上的线段的长度。
观察图形,可以看到点$C$通过线段$CD$垂直落到直线$l$上,因此线段$CD$的长度就是点$C$到直线$l$的距离。
【答案】:C.线段$CD$的长。
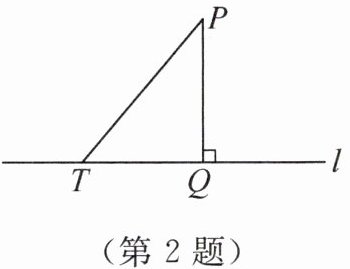
2. 如图,P是直线l外一点,$PQ⊥l$,垂足为Q,T是直线l上的一个动点,连接PT,则下列判断正确的是 (
A.$PT≥2PQ$
B.$PT≤2PQ$
C.$PT≥PQ$
D.$PT≤PQ$
]
C
)
A.$PT≥2PQ$
B.$PT≤2PQ$
C.$PT≥PQ$
D.$PT≤PQ$
]
答案:【解析】:本题可根据垂线段的性质来判断$PT$与$PQ$的大小关系。
垂线段的性质为:从直线外一点到这条直线所作的垂线段最短。
在本题中,$P$是直线$l$外一点,$PQ\perp l$,$T$是直线$l$上的一个动点,$PQ$是点$P$到直线$l$的垂线段,$PT$是点$P$到直线$l$上一点$T$的线段。
根据垂线段最短可知,$PT$的长度大于或等于$PQ$的长度,即$PT\geq PQ$。
【答案】:C
垂线段的性质为:从直线外一点到这条直线所作的垂线段最短。
在本题中,$P$是直线$l$外一点,$PQ\perp l$,$T$是直线$l$上的一个动点,$PQ$是点$P$到直线$l$的垂线段,$PT$是点$P$到直线$l$上一点$T$的线段。
根据垂线段最短可知,$PT$的长度大于或等于$PQ$的长度,即$PT\geq PQ$。
【答案】:C
3. (2025·江苏扬州期末)在体育课上,某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量图中线段
]

PC
的长.]

答案:【解析】:
本题考查垂线段最短的性质。
根据垂线段最短的性质,测量该同学的实际立定跳远成绩时,应测量图中线段$PC$的长,因为$PC$是从点$P$到起跳线$l$的垂线段。
【答案】:
$PC$
本题考查垂线段最短的性质。
根据垂线段最短的性质,测量该同学的实际立定跳远成绩时,应测量图中线段$PC$的长,因为$PC$是从点$P$到起跳线$l$的垂线段。
【答案】:
$PC$
4. 如图,点A,B,C在直线l上,$PB⊥l$,$PA= 6cm$,$PB= 5cm$,$PC= 7cm$,则点P到直线l的距离是
5
cm.答案:【解析】:本题主要考查了点到直线的距离的定义。
根据点到直线的距离的定义,即从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离。
在本题中,已知$PB\perp l$,这意味着线段$PB$是点$P$到直线$l$的垂线段。
同时,题目还给出了$PA = 6cm$,$PB = 5cm$,$PC = 7cm$,需要求点$P$到直线$l$的距离。
由于$PB$是点$P$到直线$l$的垂线段,根据点到直线的距离的定义,点$P$到直线$l$的距离就是垂线段$PB$的长度。
因此,点$P$到直线$l$的距离是$5cm$。
【答案】:$5$。
根据点到直线的距离的定义,即从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离。
在本题中,已知$PB\perp l$,这意味着线段$PB$是点$P$到直线$l$的垂线段。
同时,题目还给出了$PA = 6cm$,$PB = 5cm$,$PC = 7cm$,需要求点$P$到直线$l$的距离。
由于$PB$是点$P$到直线$l$的垂线段,根据点到直线的距离的定义,点$P$到直线$l$的距离就是垂线段$PB$的长度。
因此,点$P$到直线$l$的距离是$5cm$。
【答案】:$5$。
5. 新素养 几何直观 如图,P是$∠AOB$的边OB上一点.
(1) 过点P画OB的垂线,交OA于点C,过点P画OA的垂线,垂足为H;
(2) 线段PH的长度是点P到
]

(1) 过点P画OB的垂线,交OA于点C,过点P画OA的垂线,垂足为H;
(2) 线段PH的长度是点P到
OA
的距离,CP
是点C到直线OB的距离,线段PC,PH,OC长度之间的大小关系是PH<PC<OC
.(用“<”号连接)]

答案:【解析】:本题可根据点到直线的距离的定义以及垂线段最短的性质来求解。
点到直线的距离的定义:从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离。
垂线段最短的性质:直线外一点与直线上各点连接的所有线段中,垂线段最短。
【答案】:(1) 图略(按照题目要求,过点$P$画$OB$的垂线交$OA$于点$C$,过点$P$画$OA$的垂线,垂足为$H$)。
(2) 因为从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离,所以线段$PH$的长度是点$P$到$OA$的距离;$CP$的长度是点$C$到直线$OB$的距离。
根据垂线段最短的性质可知,直线外一点与直线上各点连接的所有线段中,垂线段最短,所以$PH<PC<OC$。
故答案依次为:$OA$;$CP$;$PH<PC<OC$。
点到直线的距离的定义:从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离。
垂线段最短的性质:直线外一点与直线上各点连接的所有线段中,垂线段最短。
【答案】:(1) 图略(按照题目要求,过点$P$画$OB$的垂线交$OA$于点$C$,过点$P$画$OA$的垂线,垂足为$H$)。
(2) 因为从直线外一点到这条直线所作的垂线段最短,这条垂线段的长度叫做这点到直线的距离,所以线段$PH$的长度是点$P$到$OA$的距离;$CP$的长度是点$C$到直线$OB$的距离。
根据垂线段最短的性质可知,直线外一点与直线上各点连接的所有线段中,垂线段最短,所以$PH<PC<OC$。
故答案依次为:$OA$;$CP$;$PH<PC<OC$。
6. 如图,长度能表示点到直线距离的线段共有 (
A.2条
B.3条
C.4条
D.5条
]
C
)A.2条
B.3条
C.4条
D.5条
]
答案:解:根据点到直线距离的定义,即从直线外一点到这条直线所作的垂线段的长度。
点A到直线BC的垂线段是AB;
点C到直线AB的垂线段是CB;
点D到直线AB的垂线段是DB;
点B到直线CD的垂线段是BD。
共有4条。
答案:C
点A到直线BC的垂线段是AB;
点C到直线AB的垂线段是CB;
点D到直线AB的垂线段是DB;
点B到直线CD的垂线段是BD。
共有4条。
答案:C
7. 如图,P是直线a外一点,过点P画$PA⊥a$于点A,在直线a上取一点B,连接PB,使$PB= \frac {3}{2}PA$,点C在线段AB上,连接PC.若$PA= 4$,则线段PC的长不可能是 (

A.3.8
B.4.9
C.5.6
D.5.9
]
A
)
A.3.8
B.4.9
C.5.6
D.5.9
]
答案:【解析】:本题考查垂线段最短的性质。
已知$PA\perp a$,$PA = 4$,且$PB=\frac{3}{2}PA$,所以$PB=\frac{3}{2}×4 = 6$。
根据垂线段最短的性质,在连接点$P$与直线$a$上各点的线段中,$PA$是最短的。
点$C$在线段$AB$上,那么$PC$的长度范围是$PA\leqslant PC\leqslant PB$,即$4\leqslant PC\leqslant 6$。
逐一分析选项:
选项A:$3.8\lt 4$,不满足$4\leqslant PC\leqslant 6$,所以该选项符合题意。
选项B:$4\lt 4.9\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
选项C:$4\lt 5.6\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
选项D:$4\lt 5.9\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
【答案】:A
已知$PA\perp a$,$PA = 4$,且$PB=\frac{3}{2}PA$,所以$PB=\frac{3}{2}×4 = 6$。
根据垂线段最短的性质,在连接点$P$与直线$a$上各点的线段中,$PA$是最短的。
点$C$在线段$AB$上,那么$PC$的长度范围是$PA\leqslant PC\leqslant PB$,即$4\leqslant PC\leqslant 6$。
逐一分析选项:
选项A:$3.8\lt 4$,不满足$4\leqslant PC\leqslant 6$,所以该选项符合题意。
选项B:$4\lt 4.9\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
选项C:$4\lt 5.6\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
选项D:$4\lt 5.9\lt 6$,满足$4\leqslant PC\leqslant 6$,所以该选项不符合题意。
【答案】:A