1. 如图,在平面内作已知直线m的垂线,可作的垂线有(
A.0条
B.1条
C.2条
D.无数条
D
)A.0条
B.1条
C.2条
D.无数条
答案:【解析】:
本题考查垂直的定义及性质。
在平面内,一条直线有无数条垂线,因为可以在直线上的任意一点作垂线,并且这些垂线都是不同的。
【答案】:D. 无数条
本题考查垂直的定义及性质。
在平面内,一条直线有无数条垂线,因为可以在直线上的任意一点作垂线,并且这些垂线都是不同的。
【答案】:D. 无数条
2. 如图,$AC⊥BC$,直线EF经过点C. 若$∠1= 35^{\circ }$,则$∠2$的度数为
$55^{\circ}$
.答案:【解析】:本题主要考查了垂直的定义以及角的计算。
因为$AC\perp BC$,根据垂直的定义,可知$\angle ACB = 90^{\circ}$。
又因为$\angle 1 = 35^{\circ}$,且$\angle ACB=\angle 1+\angle ACF = 90^{\circ}$,所以$\angle ACF=90^{\circ}-\angle 1$。
而$\angle 2$与$\angle ACF$是对顶角,根据对顶角相等的性质,可得$\angle 2=\angle ACF$。
那么$\angle 2 = 90^{\circ}-\angle 1=90^{\circ}-35^{\circ}=55^{\circ}$。
【答案】:$55^{\circ}$
因为$AC\perp BC$,根据垂直的定义,可知$\angle ACB = 90^{\circ}$。
又因为$\angle 1 = 35^{\circ}$,且$\angle ACB=\angle 1+\angle ACF = 90^{\circ}$,所以$\angle ACF=90^{\circ}-\angle 1$。
而$\angle 2$与$\angle ACF$是对顶角,根据对顶角相等的性质,可得$\angle 2=\angle ACF$。
那么$\angle 2 = 90^{\circ}-\angle 1=90^{\circ}-35^{\circ}=55^{\circ}$。
【答案】:$55^{\circ}$
3. 如图,直线AB,CD相交于点O,$EO⊥AB,∠EOD= 50^{\circ }$,则$∠BOC= $
$140^{\circ}$
.答案:【解析】:
本题主要考查垂直的定义、对顶角和邻补角的特征。
已知$EO\perp AB$,根据垂直的定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,所以$\angle EOB = 90^{\circ}$。
又已知$\angle EOD = 50^{\circ}$,因为$\angle EOB=\angle EOD+\angle DOB$,所以$\angle DOB=\angle EOB - \angle EOD$,将$\angle EOB = 90^{\circ}$,$\angle EOD = 50^{\circ}$代入可得:$\angle DOB = 90^{\circ} - 50^{\circ} = 40^{\circ}$。
根据对顶角的性质,对顶角是指如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,对顶角相等。
因为$\angle BOC$与$\angle AOD$是对顶角,$\angle DOB$与$\angle AOC$是对顶角,所以$\angle BOC$与$\angle AOD$相等,$\angle DOB$与$\angle AOC$相等;
根据邻补角的性质,邻补角是指两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角叫做互为邻补角,邻补角之和为$180^{\circ}$。
因为$\angle DOB$与$\angle BOC$是邻补角,所以$\angle BOC = 180^{\circ} - \angle DOB$,将$\angle DOB = 40^{\circ}$代入可得:$\angle BOC = 180^{\circ} - 40^{\circ} = 140^{\circ}$。
【答案】:
$140^{\circ}$
本题主要考查垂直的定义、对顶角和邻补角的特征。
已知$EO\perp AB$,根据垂直的定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,所以$\angle EOB = 90^{\circ}$。
又已知$\angle EOD = 50^{\circ}$,因为$\angle EOB=\angle EOD+\angle DOB$,所以$\angle DOB=\angle EOB - \angle EOD$,将$\angle EOB = 90^{\circ}$,$\angle EOD = 50^{\circ}$代入可得:$\angle DOB = 90^{\circ} - 50^{\circ} = 40^{\circ}$。
根据对顶角的性质,对顶角是指如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,对顶角相等。
因为$\angle BOC$与$\angle AOD$是对顶角,$\angle DOB$与$\angle AOC$是对顶角,所以$\angle BOC$与$\angle AOD$相等,$\angle DOB$与$\angle AOC$相等;
根据邻补角的性质,邻补角是指两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角叫做互为邻补角,邻补角之和为$180^{\circ}$。
因为$\angle DOB$与$\angle BOC$是邻补角,所以$\angle BOC = 180^{\circ} - \angle DOB$,将$\angle DOB = 40^{\circ}$代入可得:$\angle BOC = 180^{\circ} - 40^{\circ} = 140^{\circ}$。
【答案】:
$140^{\circ}$
4. 如图,已知$OA⊥OB,OC⊥OD,∠COE= ∠BOE$,OF平分$∠AOD$,给出下列结论:①$∠AOE= ∠DOE$;②$∠AOD+∠COB= 180^{\circ }$;③$∠COB-∠AOD= 90^{\circ }$;④$∠COE+∠BOF= 180^{\circ }$. 其中正确的有(
A.4个
B.3个
C.2个
D.0个
B
)A.4个
B.3个
C.2个
D.0个
答案:【解析】:本题可根据垂直的性质、角平分线的定义以及角的和差关系来逐一分析各个结论。
结论①:判断$\angle AOE = \angle DOE$是否成立
已知$OA\perp OB$,$OC\perp OD$,则$\angle AOB = \angle COD = 90^{\circ}$。
因为$\angle AOB + \angle AOD + \angle DOC + \angle COB = 360^{\circ}$,所以$\angle AOD + \angle COB = 360^{\circ} - \angle AOB - \angle DOC = 360^{\circ} - 90^{\circ} - 90^{\circ} = 180^{\circ}$。
又因为$\angle COE = \angle BOE$,即$\angle BOE$和$\angle COE$将$\angle BOC$平分,那么$\angle AOE - \angle BOE = \angle DOE - \angle COE$,所以$\angle AOE = \angle DOE$,故①正确。
结论②:判断$\angle AOD + \angle COB = 180^{\circ}$是否成立
由上述分析可知,因为$\angle AOB = \angle COD = 90^{\circ}$,且$\angle AOB + \angle AOD + \angle DOC + \angle COB = 360^{\circ}$,所以$\angle AOD + \angle COB = 360^{\circ} - 90^{\circ} - 90^{\circ} = 180^{\circ}$,故②正确。
结论③:判断$\angle COB - \angle AOD = 90^{\circ}$是否成立
由$\angle AOD + \angle COB = 180^{\circ}$,移项可得$\angle COB = 180^{\circ} - \angle AOD$,那么$\angle COB - \angle AOD = 180^{\circ} - 2\angle AOD$,只有当$\angle AOD = 45^{\circ}$时,$\angle COB - \angle AOD = 90^{\circ}$,一般情况下不成立,故③错误。
结论④:判断$\angle COE + \angle BOF = 180^{\circ}$是否成立
因为$OF$平分$\angle AOD$,所以$\angle AOF = \angle DOF = \frac{1}{2}\angle AOD$。
由$\angle AOD + \angle COB = 180^{\circ}$,可得$\angle AOD = 180^{\circ} - \angle COB$。
又因为$\angle COE = \angle BOE$,$\angle BOC = \angle BOE + \angle COE = 2\angle COE$。
$\angle BOF = \angle BOA + \angle AOF = 90^{\circ} + \frac{1}{2}\angle AOD = 90^{\circ} + \frac{1}{2}(180^{\circ} - \angle COB)= 180^{\circ} - \frac{1}{2}\angle BOC$。
而$\angle COE = \frac{1}{2}\angle BOC$,所以$\angle COE + \angle BOF = \frac{1}{2}\angle BOC + 180^{\circ} - \frac{1}{2}\angle BOC = 180^{\circ}$,故④正确。
综上,①②④正确,共$3$个,答案选B。
【答案】:B
结论①:判断$\angle AOE = \angle DOE$是否成立
已知$OA\perp OB$,$OC\perp OD$,则$\angle AOB = \angle COD = 90^{\circ}$。
因为$\angle AOB + \angle AOD + \angle DOC + \angle COB = 360^{\circ}$,所以$\angle AOD + \angle COB = 360^{\circ} - \angle AOB - \angle DOC = 360^{\circ} - 90^{\circ} - 90^{\circ} = 180^{\circ}$。
又因为$\angle COE = \angle BOE$,即$\angle BOE$和$\angle COE$将$\angle BOC$平分,那么$\angle AOE - \angle BOE = \angle DOE - \angle COE$,所以$\angle AOE = \angle DOE$,故①正确。
结论②:判断$\angle AOD + \angle COB = 180^{\circ}$是否成立
由上述分析可知,因为$\angle AOB = \angle COD = 90^{\circ}$,且$\angle AOB + \angle AOD + \angle DOC + \angle COB = 360^{\circ}$,所以$\angle AOD + \angle COB = 360^{\circ} - 90^{\circ} - 90^{\circ} = 180^{\circ}$,故②正确。
结论③:判断$\angle COB - \angle AOD = 90^{\circ}$是否成立
由$\angle AOD + \angle COB = 180^{\circ}$,移项可得$\angle COB = 180^{\circ} - \angle AOD$,那么$\angle COB - \angle AOD = 180^{\circ} - 2\angle AOD$,只有当$\angle AOD = 45^{\circ}$时,$\angle COB - \angle AOD = 90^{\circ}$,一般情况下不成立,故③错误。
结论④:判断$\angle COE + \angle BOF = 180^{\circ}$是否成立
因为$OF$平分$\angle AOD$,所以$\angle AOF = \angle DOF = \frac{1}{2}\angle AOD$。
由$\angle AOD + \angle COB = 180^{\circ}$,可得$\angle AOD = 180^{\circ} - \angle COB$。
又因为$\angle COE = \angle BOE$,$\angle BOC = \angle BOE + \angle COE = 2\angle COE$。
$\angle BOF = \angle BOA + \angle AOF = 90^{\circ} + \frac{1}{2}\angle AOD = 90^{\circ} + \frac{1}{2}(180^{\circ} - \angle COB)= 180^{\circ} - \frac{1}{2}\angle BOC$。
而$\angle COE = \frac{1}{2}\angle BOC$,所以$\angle COE + \angle BOF = \frac{1}{2}\angle BOC + 180^{\circ} - \frac{1}{2}\angle BOC = 180^{\circ}$,故④正确。
综上,①②④正确,共$3$个,答案选B。
【答案】:B
5. 已知$∠BOC= 60^{\circ }$,OF平分$∠BOC$. 若$AO⊥BO$,OE平分$∠AOC$,则$∠EOF= $
45°
.答案:解:情况一:射线OA在∠BOC外部
∵AO⊥BO
∴∠AOB=90°
∵∠BOC=60°
∴∠AOC=∠AOB+∠BOC=150°
∵OE平分∠AOC
∴∠COE=∠AOC/2=75°
∵OF平分∠BOC
∴∠COF=∠BOC/2=30°
∴∠EOF=∠COE-∠COF=45°
情况二:射线OA在∠BOC内部
∵AO⊥BO
∴∠AOB=90°
∵∠BOC=60°,∠AOB>∠BOC
∴此情况不存在
综上,∠EOF=45°
∵AO⊥BO
∴∠AOB=90°
∵∠BOC=60°
∴∠AOC=∠AOB+∠BOC=150°
∵OE平分∠AOC
∴∠COE=∠AOC/2=75°
∵OF平分∠BOC
∴∠COF=∠BOC/2=30°
∴∠EOF=∠COE-∠COF=45°
情况二:射线OA在∠BOC内部
∵AO⊥BO
∴∠AOB=90°
∵∠BOC=60°,∠AOB>∠BOC
∴此情况不存在
综上,∠EOF=45°
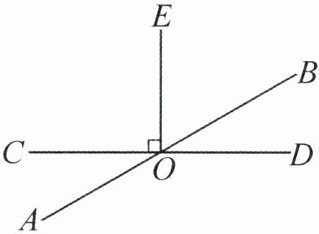
6. 如图,已知直线AB,CD相交于点O,$OE⊥CD,∠BOD:∠BOC= 1:5$.
(1)求$∠AOE$的度数;
(2)过点O作$OF⊥AB$,并求$∠EOF$的度数.
(1)求$∠AOE$的度数;
(2)过点O作$OF⊥AB$,并求$∠EOF$的度数.

答案:(1)解:因为∠BOD:∠BOC=1:5,且∠BOD+∠BOC=180°,
设∠BOD=x,则∠BOC=5x,
x+5x=180°,解得x=30°,即∠BOD=30°,
所以∠AOC=∠BOD=30°(对顶角相等),
因为OE⊥CD,所以∠COE=90°,
∠AOE=∠COE-∠AOC=90°-30°=60°。
(2)解:因为OF⊥AB,所以∠BOF=90°,
由(1)知∠BOD=30°,OE⊥CD,所以∠DOE=90°,
∠BOE=∠DOE-∠BOD=90°-30°=60°,
∠EOF=∠BOF+∠BOE=90°+60°=150°。
设∠BOD=x,则∠BOC=5x,
x+5x=180°,解得x=30°,即∠BOD=30°,
所以∠AOC=∠BOD=30°(对顶角相等),
因为OE⊥CD,所以∠COE=90°,
∠AOE=∠COE-∠AOC=90°-30°=60°。
(2)解:因为OF⊥AB,所以∠BOF=90°,
由(1)知∠BOD=30°,OE⊥CD,所以∠DOE=90°,
∠BOE=∠DOE-∠BOD=90°-30°=60°,
∠EOF=∠BOF+∠BOE=90°+60°=150°。
7. 在同一平面内,若$∠A与∠B$的两边分别垂直,且$∠A比∠B$的3倍少$40^{\circ }$,则$∠A$的度数为
$20^{\circ}$或$125^{\circ}$
.答案:【解析】:
本题主要考查垂直线的性质以及角的计算。
首先,根据题目条件,$\angle A$与$\angle B$的两边分别垂直。
在同一平面内,如果两个角的两边分别垂直,那么这两个角相等或互补。
设$\angle B = x^{\circ}$,根据题目条件,$\angle A$比$\angle B$的$3$倍少$40^{\circ}$,即:
$\angle A = 3x - 40^{\circ}$
由于$\angle A$与$\angle B$相等或互补,因此有两种可能的情况:
$\angle A = \angle B$,即$3x - 40 = x$,解得$x = 20$,则$\angle A = 20^{\circ}$。
$\angle A + \angle B = 180^{\circ}$,即$3x - 40 + x = 180$,解得$x = 55$,则$\angle A = 125^{\circ}$。
所以,$\angle A$的度数为$20^{\circ}$或$125^{\circ}$。
【答案】:
$20^{\circ}$或$125^{\circ}$。
本题主要考查垂直线的性质以及角的计算。
首先,根据题目条件,$\angle A$与$\angle B$的两边分别垂直。
在同一平面内,如果两个角的两边分别垂直,那么这两个角相等或互补。
设$\angle B = x^{\circ}$,根据题目条件,$\angle A$比$\angle B$的$3$倍少$40^{\circ}$,即:
$\angle A = 3x - 40^{\circ}$
由于$\angle A$与$\angle B$相等或互补,因此有两种可能的情况:
$\angle A = \angle B$,即$3x - 40 = x$,解得$x = 20$,则$\angle A = 20^{\circ}$。
$\angle A + \angle B = 180^{\circ}$,即$3x - 40 + x = 180$,解得$x = 55$,则$\angle A = 125^{\circ}$。
所以,$\angle A$的度数为$20^{\circ}$或$125^{\circ}$。
【答案】:
$20^{\circ}$或$125^{\circ}$。
8. 已知OC是从直线AB上一点O引出的任意一条射线,OE平分$∠AOC$,沿顺时针方向画$∠EOF$,以O为端点引射线OD,使得OF平分$∠BOD$.
(1)如图①,若$∠EOF= 135^{\circ }$,判断OC与OD之间的位置关系,并说明理由;
(2)如图②,若$∠EOF= 45^{\circ }$,则OC与OD之间的位置关系是否发生变化?并说明理由.


(1)如图①,若$∠EOF= 135^{\circ }$,判断OC与OD之间的位置关系,并说明理由;
(2)如图②,若$∠EOF= 45^{\circ }$,则OC与OD之间的位置关系是否发生变化?并说明理由.


答案:【解析】:本题主要考查了角平分线的性质以及利用角的运算来判断直线的位置关系。
(1)首先根据角平分线的性质得到$\angle EOC$与$\angle AOC$、$\angle DOF$与$\angle BOD$的关系,再通过$\angle EOF$的度数求出$\angle COD$的度数,进而判断$OC$与$OD$的位置关系。
(2)同样利用角平分线的性质,结合$\angle EOF$的度数求出$\angle COD$的度数,判断其是否变化。
(1)$OC\perp OD$,理由如下:
因为$OE$平分$\angle AOC$,所以$\angle EOC = \frac{1}{2}\angle AOC$;
因为$OF$平分$\angle BOD$,所以$\angle DOF = \frac{1}{2}\angle BOD$。
又因为$\angle EOF = 135^{\circ}$,所以$\angle EOC + \angle DOF = 180^{\circ} - \angle EOF = 180^{\circ} - 135^{\circ} = 45^{\circ}$。
那么$\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOD = 45^{\circ}$,即$\frac{1}{2}(\angle AOC + \angle BOD) = 45^{\circ}$。
因为$\angle AOC + \angle BOD + \angle COD = 180^{\circ}$,且$\angle AOC + \angle BOD = 90^{\circ}$,所以$\angle COD = 180^{\circ} - 90^{\circ} = 90^{\circ}$,所以$OC\perp OD$。
(2)$OC$与$OD$之间的位置关系没有发生变化,理由如下:
因为$OE$平分$\angle AOC$,所以$\angle EOC = \frac{1}{2}\angle AOC$;
因为$OF$平分$\angle BOD$,所以$\angle DOF = \frac{1}{2}\angle BOD$。
已知$\angle EOF = 45^{\circ}$,则$\angle EOC + \angle DOF = 180^{\circ} - \angle EOF = 180^{\circ} - 45^{\circ} = 135^{\circ}$。
所以$\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOD = 135^{\circ}$,即$\frac{1}{2}(\angle AOC + \angle BOD) = 135^{\circ}$。
那么$\angle AOC + \angle BOD = 270^{\circ}$。
又因为$\angle AOC + \angle BOD + \angle COD = 360^{\circ}$,所以$\angle COD = 360^{\circ} - 270^{\circ} = 90^{\circ}$,所以$OC\perp OD$,位置关系没有发生变化。
【答案】:
(1)$OC\perp OD$,理由:因为$OE$平分$\angle AOC$,$OF$平分$\angle BOD$,$\angle EOF = 135^{\circ}$,通过角的运算可得$\angle COD = 90^{\circ}$,所以$OC\perp OD$。
(2)$OC$与$OD$之间的位置关系没有发生变化,理由:同样根据角平分线的性质和角的运算,得出$\angle COD = 90^{\circ}$,所以$OC\perp OD$,位置关系不变。
(1)首先根据角平分线的性质得到$\angle EOC$与$\angle AOC$、$\angle DOF$与$\angle BOD$的关系,再通过$\angle EOF$的度数求出$\angle COD$的度数,进而判断$OC$与$OD$的位置关系。
(2)同样利用角平分线的性质,结合$\angle EOF$的度数求出$\angle COD$的度数,判断其是否变化。
(1)$OC\perp OD$,理由如下:
因为$OE$平分$\angle AOC$,所以$\angle EOC = \frac{1}{2}\angle AOC$;
因为$OF$平分$\angle BOD$,所以$\angle DOF = \frac{1}{2}\angle BOD$。
又因为$\angle EOF = 135^{\circ}$,所以$\angle EOC + \angle DOF = 180^{\circ} - \angle EOF = 180^{\circ} - 135^{\circ} = 45^{\circ}$。
那么$\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOD = 45^{\circ}$,即$\frac{1}{2}(\angle AOC + \angle BOD) = 45^{\circ}$。
因为$\angle AOC + \angle BOD + \angle COD = 180^{\circ}$,且$\angle AOC + \angle BOD = 90^{\circ}$,所以$\angle COD = 180^{\circ} - 90^{\circ} = 90^{\circ}$,所以$OC\perp OD$。
(2)$OC$与$OD$之间的位置关系没有发生变化,理由如下:
因为$OE$平分$\angle AOC$,所以$\angle EOC = \frac{1}{2}\angle AOC$;
因为$OF$平分$\angle BOD$,所以$\angle DOF = \frac{1}{2}\angle BOD$。
已知$\angle EOF = 45^{\circ}$,则$\angle EOC + \angle DOF = 180^{\circ} - \angle EOF = 180^{\circ} - 45^{\circ} = 135^{\circ}$。
所以$\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOD = 135^{\circ}$,即$\frac{1}{2}(\angle AOC + \angle BOD) = 135^{\circ}$。
那么$\angle AOC + \angle BOD = 270^{\circ}$。
又因为$\angle AOC + \angle BOD + \angle COD = 360^{\circ}$,所以$\angle COD = 360^{\circ} - 270^{\circ} = 90^{\circ}$,所以$OC\perp OD$,位置关系没有发生变化。
【答案】:
(1)$OC\perp OD$,理由:因为$OE$平分$\angle AOC$,$OF$平分$\angle BOD$,$\angle EOF = 135^{\circ}$,通过角的运算可得$\angle COD = 90^{\circ}$,所以$OC\perp OD$。
(2)$OC$与$OD$之间的位置关系没有发生变化,理由:同样根据角平分线的性质和角的运算,得出$\angle COD = 90^{\circ}$,所以$OC\perp OD$,位置关系不变。