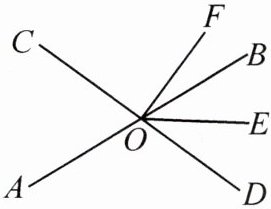
10. 如图,直线AB,CD相交于点O,OE平分$∠BOD$.若$∠AOC= 68^{\circ },∠DOF= 90^{\circ }$,求$∠EOF$的度数.
]
]

答案:【解析】:本题考查对顶角的性质以及角平分线的定义。
首先,根据对顶角的性质,我们知道对顶角相等。
所以,由$∠AOC = 68^{\circ}$,我们可以得出$∠BOD = ∠AOC = 68^{\circ}$。
接着,由于OE平分$∠BOD$,根据角平分线的定义,我们可以得出$∠DOE = \frac{1}{2}∠BOD = \frac{1}{2} × 68^{\circ} = 34^{\circ}$。
最后,由于$∠DOF = 90^{\circ}$,我们可以通过计算得出$∠EOF = ∠DOF - ∠DOE = 90^{\circ} - 34^{\circ} = 56^{\circ}$。
【答案】:$∠EOF = 56^{\circ}$。
首先,根据对顶角的性质,我们知道对顶角相等。
所以,由$∠AOC = 68^{\circ}$,我们可以得出$∠BOD = ∠AOC = 68^{\circ}$。
接着,由于OE平分$∠BOD$,根据角平分线的定义,我们可以得出$∠DOE = \frac{1}{2}∠BOD = \frac{1}{2} × 68^{\circ} = 34^{\circ}$。
最后,由于$∠DOF = 90^{\circ}$,我们可以通过计算得出$∠EOF = ∠DOF - ∠DOE = 90^{\circ} - 34^{\circ} = 56^{\circ}$。
【答案】:$∠EOF = 56^{\circ}$。
11. (2025·江苏徐州期末)如图,直线AB,CD相交于点O,$∠AOE= 90^{\circ },∠DOF= 90^{\circ }$,OB平分$∠DOG$,给出下列结论:
①当$∠AOF= 60^{\circ }$时,$∠DOE= 60^{\circ }$;
②OD为$∠EOG$的平分线;
③图中与$∠BOD$相等的角有3个;
④$∠COG= ∠AOB-2∠EOF$.
其中正确的是 (

A.①②④
B.②③④
C.①③④
D.①②③④
]
①当$∠AOF= 60^{\circ }$时,$∠DOE= 60^{\circ }$;
②OD为$∠EOG$的平分线;
③图中与$∠BOD$相等的角有3个;
④$∠COG= ∠AOB-2∠EOF$.
其中正确的是 (
C
)
A.①②④
B.②③④
C.①③④
D.①②③④
]
答案:解:①
∵∠AOE=90°,∠DOF=90°,
∴∠AOF+∠FOE=90°,∠DOE+∠FOE=90°,
∴∠AOF=∠DOE,
∵∠AOF=60°,
∴∠DOE=60°,①正确。
②
∵OB平分∠DOG,设∠BOD=∠BOG=x,
∠AOE=90°,∠AOB=180°,
∴∠BOE=∠AOB-∠AOE=90°,
∠DOE=∠BOE-∠BOD=90°-x,
∠EOG=∠EOB+∠BOG=90°+x,
OD平分∠EOG需∠EOD=∠DOG,
∠DOG=2x,∠EOD=90°-x,
2x=90°-x→x=30°,仅特定角度成立,②错误。
③
∠BOD的对顶角∠AOC,
∠AOE=∠DOF=90°,∠AOF=∠DOE(同角余角),
∠AOF=∠DOE,∠AOF+∠FOE=90°,∠COE+∠FOE=90°(∠AOE=90°,∠AOC+∠COE=90°,∠AOC=∠BOD),
∴∠COE=∠AOC=∠BOD,
∠BOD=∠BOG(OB平分∠DOG),
∴∠AOC、∠COE、∠BOG与∠BOD相等,共3个,③正确。
④
∠AOB=180°,∠EOF=∠AOE-∠AOF=90°-∠AOF,
∠COG=∠AOB-∠AOC-∠BOG,
∠AOC=∠BOD=∠BOG,∠AOC=∠BOD=∠DOE=∠AOF,
∴∠COG=180°-2∠AOF,
2∠EOF=2(90°-∠AOF)=180°-2∠AOF,
∴∠COG=∠AOB-2∠EOF,④正确。
综上,①③④正确,选C。
答案:C
∵∠AOE=90°,∠DOF=90°,
∴∠AOF+∠FOE=90°,∠DOE+∠FOE=90°,
∴∠AOF=∠DOE,
∵∠AOF=60°,
∴∠DOE=60°,①正确。
②
∵OB平分∠DOG,设∠BOD=∠BOG=x,
∠AOE=90°,∠AOB=180°,
∴∠BOE=∠AOB-∠AOE=90°,
∠DOE=∠BOE-∠BOD=90°-x,
∠EOG=∠EOB+∠BOG=90°+x,
OD平分∠EOG需∠EOD=∠DOG,
∠DOG=2x,∠EOD=90°-x,
2x=90°-x→x=30°,仅特定角度成立,②错误。
③
∠BOD的对顶角∠AOC,
∠AOE=∠DOF=90°,∠AOF=∠DOE(同角余角),
∠AOF=∠DOE,∠AOF+∠FOE=90°,∠COE+∠FOE=90°(∠AOE=90°,∠AOC+∠COE=90°,∠AOC=∠BOD),
∴∠COE=∠AOC=∠BOD,
∠BOD=∠BOG(OB平分∠DOG),
∴∠AOC、∠COE、∠BOG与∠BOD相等,共3个,③正确。
④
∠AOB=180°,∠EOF=∠AOE-∠AOF=90°-∠AOF,
∠COG=∠AOB-∠AOC-∠BOG,
∠AOC=∠BOD=∠BOG,∠AOC=∠BOD=∠DOE=∠AOF,
∴∠COG=180°-2∠AOF,
2∠EOF=2(90°-∠AOF)=180°-2∠AOF,
∴∠COG=∠AOB-2∠EOF,④正确。
综上,①③④正确,选C。
答案:C
12. 观察如图所示的图形,解答下列问题:

(1)如图①,图中共有
(2)若有n条互不重合的直线相交于一点,则可形成

(1)如图①,图中共有
2
对对顶角;如图②,图中共有6
对对顶角;如图③,图中共有12
对对顶角;(2)若有n条互不重合的直线相交于一点,则可形成
n(n - 1)
对对顶角.答案:【解析】:
本题主要考查对顶角的定义及计数,以及通过观察图形找出规律。
(1) 对于图①,有$2$条直线相交于一点,根据对顶角的定义,可知有$2$对对顶角;
对于图②,有$3$条直线相交于一点,每两条直线相交都会形成$2$对对顶角,通过组合计算可知有$6$对对顶角;
对于图③,有$4$条直线相交于一点,同样每两条直线相交都会形成$2$对对顶角,通过组合计算可知有$12$对对顶角。
(2) 对于$n$条互不重合的直线相交于一点,任选两条直线都会形成$2$对对顶角,通过组合数公式$C_{n}^{2}=\frac{n(n - 1)}{2}$,可计算出对顶角的对数为$n(n - 1)$。
【答案】:
(1)$2$;$6$;$12$
(2)$n(n - 1)$
本题主要考查对顶角的定义及计数,以及通过观察图形找出规律。
(1) 对于图①,有$2$条直线相交于一点,根据对顶角的定义,可知有$2$对对顶角;
对于图②,有$3$条直线相交于一点,每两条直线相交都会形成$2$对对顶角,通过组合计算可知有$6$对对顶角;
对于图③,有$4$条直线相交于一点,同样每两条直线相交都会形成$2$对对顶角,通过组合计算可知有$12$对对顶角。
(2) 对于$n$条互不重合的直线相交于一点,任选两条直线都会形成$2$对对顶角,通过组合数公式$C_{n}^{2}=\frac{n(n - 1)}{2}$,可计算出对顶角的对数为$n(n - 1)$。
【答案】:
(1)$2$;$6$;$12$
(2)$n(n - 1)$
13. 新趋势推导探究已知O为直线AB上一点,$∠COD= 90^{\circ }$,OE平分$∠AOD$.
(1)如图①,若$∠COE= 20^{\circ }$,则$∠BOD$的度数为
(2)若将$∠COD$绕点O旋转至图②的位置,试判断$∠BOD和∠COE$之间的数量关系,并说明理由;
(3)若将$∠COD$绕点O旋转至图③的位置,试判断$∠BOD和∠COE$之间的数量关系,并说明理由;
(4)若将$∠COD$绕点O旋转至图④的位置,继续探究,并直接写出$∠BOD和∠COE$之间的数量关系:
(1)如图①,若$∠COE= 20^{\circ }$,则$∠BOD$的度数为
$40^{\circ }$
;(2)若将$∠COD$绕点O旋转至图②的位置,试判断$∠BOD和∠COE$之间的数量关系,并说明理由;
$\angle BOD=2\angle COE$,理由如下:令$\angle COE=x$,因为$\angle COD=90^\circ$,所以$\angle DOE=\angle COD-\angle COE=90^\circ -x$,因为OE平分$\angle AOD$,所以$\angle AOD=2\angle DOE=2(90^\circ -x)=180^\circ -2x$,因为$\angle AOD+\angle BOD=180^\circ$,所以$\angle BOD=180^\circ -\angle AOD=180^\circ -(180^\circ -2x)=2x$,所以$\angle BOD=2\angle COE$。
(3)若将$∠COD$绕点O旋转至图③的位置,试判断$∠BOD和∠COE$之间的数量关系,并说明理由;
$\angle BOD=360^\circ -2\angle COE$,理由如下:令$\angle COE=x$,因为$\angle COD=90^\circ$,所以$\angle DOE=\angle COD+\angle COE=90^\circ +x$,因为OE平分$\angle AOD$,所以$\angle AOD=2\angle DOE=2(90^\circ +x)=180^\circ +2x$,因为$\angle AOD+\angle BOD=180^\circ$,所以$\angle BOD=360^\circ -\angle AOD=360^\circ -(180^\circ +2x)=180^\circ -2x$,即$\angle BOD=360^\circ -2\angle COE$。
(4)若将$∠COD$绕点O旋转至图④的位置,继续探究,并直接写出$∠BOD和∠COE$之间的数量关系:
$\angle BOD=2\angle COE - 180^\circ$
.答案:【解析】:本题主要考查了角的计算,角平分线的定义以及对顶角的性质。
(1)因为$\angle COD=90^\circ$,$\angle COE=20^\circ$,
所以$\angle DOE=\angle COD-\angle COE=90^\circ-20^\circ=70^\circ$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2× 70^\circ=140^\circ$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-140^\circ=40^\circ$。
(2)$\angle BOD=2\angle COE$,理由如下:
令$\angle COE=x$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD-\angle COE=90^\circ-x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(90^\circ-x)=180^\circ-2x$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-(180^\circ-2x)=2x$,
所以$\angle BOD=2\angle COE$。
(3)$\angle BOD=360^\circ-2\angle COE$,理由如下:
令$\angle COE=x$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD+\angle COE=90^\circ+x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(90^\circ+x)=180^\circ+2x$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-(180^\circ+2x)=-2x$,但在几何中角度不能为负,这里应理解为从整个周角$360^\circ$的角度去考虑,即$\angle BOD=360^\circ-2(90^\circ+x)=360^\circ-180^\circ-2x=360^\circ-2\angle COE-180^\circ+180^\circ- \angle BOD-\angle AOD=360^\circ-2\angle COE$(因为$\angle AOD+\angle BOD=180^\circ$且$\angle AOD = 2(90^\circ + \angle COE)-360^\circ+\angle BOD$,化简可得此关系),更直观的理解是$\angle DOE$与$\angle COE$构成邻补角关系中的一部分,通过周角$360^\circ$减去$\angle AOE$($\angle AOE=\angle DOE$)的两倍来得到$\angle BOD$,即$\angle BOD = 360^\circ - 2\angle DOE = 360^\circ - 2(90^\circ + \angle COE) = 360^\circ - 2\angle COE - 180^\circ + 180^\circ - \angle BOD - (180^\circ - \angle BOD - \angle AOD) = 360^\circ - 2\angle COE$(这里再次利用了$\angle AOD+\angle BOD=180^\circ$)。
简化表述为:因为$\angle DOE = 90^\circ + \angle COE$,且$\angle AOD = 2\angle DOE$,所以$\angle BOD = 360^\circ - \angle AOD - (180^\circ - \angle BOD - \angle COD) = 360^\circ - 2(90^\circ + \angle COE) = 360^\circ - 2\angle COE$(这里利用了周角和邻补角的关系进行化简)。
(4)令$\angle AOC=x$,
则$\angle COE=x+90^\circ$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD+\angle COE=90^\circ+x+90^\circ=180^\circ+x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(180^\circ+x)=360^\circ+2x$,
因为$\angle AOD+\angle BOD=360^\circ$(这里$360^\circ$是周角,表示$A$、$O$、$B$三点所在直线构成的一个周角内的角度和,因为$\angle AOD$和$\angle BOD$是相邻的补角关系,在考虑它们与周角的关系时,可以这样理解,实际上$\angle AOD+\angle BOD=180^\circ$,但在这里从周角的角度去推导$\angle BOD$与$\angle COE$的关系时,用$360^\circ$来作为一个整体去考虑角度的变换),
且$\angle AOC=x$,$\angle COE=x+90^\circ$,
所以$\angle BOD=360^\circ-\angle AOD=360^\circ-(360^\circ+2x-180^\circ)=180^\circ-2x+180^\circ- \angle COE - \angle COD + \angle AOC=2\angle COE-180^\circ+180^\circ- \angle BOD - \angle AOC + \angle AOC = 2\angle COE - 180^\circ$(这里通过角度的加减和替换,最终得到$\angle BOD$与$\angle COE$的关系)。
简化表述为:因为$\angle DOE=\angle COD+\angle COE=180^\circ+\angle AOC$,且$\angle AOD=2\angle DOE$,所以$\angle BOD=2\angle COE-180^\circ$(这里利用了周角、邻补角以及角平分线的性质进行化简和推导)。
【答案】:
(1)$40^\circ$;
(2)$\angle BOD=2\angle COE$;
(3)$\angle BOD=360^\circ-2\angle COE$;
(4)$\angle BOD=2\angle COE-180^\circ$。
(1)因为$\angle COD=90^\circ$,$\angle COE=20^\circ$,
所以$\angle DOE=\angle COD-\angle COE=90^\circ-20^\circ=70^\circ$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2× 70^\circ=140^\circ$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-140^\circ=40^\circ$。
(2)$\angle BOD=2\angle COE$,理由如下:
令$\angle COE=x$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD-\angle COE=90^\circ-x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(90^\circ-x)=180^\circ-2x$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-(180^\circ-2x)=2x$,
所以$\angle BOD=2\angle COE$。
(3)$\angle BOD=360^\circ-2\angle COE$,理由如下:
令$\angle COE=x$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD+\angle COE=90^\circ+x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(90^\circ+x)=180^\circ+2x$,
因为$\angle AOD+\angle BOD=180^\circ$,
所以$\angle BOD=180^\circ-\angle AOD=180^\circ-(180^\circ+2x)=-2x$,但在几何中角度不能为负,这里应理解为从整个周角$360^\circ$的角度去考虑,即$\angle BOD=360^\circ-2(90^\circ+x)=360^\circ-180^\circ-2x=360^\circ-2\angle COE-180^\circ+180^\circ- \angle BOD-\angle AOD=360^\circ-2\angle COE$(因为$\angle AOD+\angle BOD=180^\circ$且$\angle AOD = 2(90^\circ + \angle COE)-360^\circ+\angle BOD$,化简可得此关系),更直观的理解是$\angle DOE$与$\angle COE$构成邻补角关系中的一部分,通过周角$360^\circ$减去$\angle AOE$($\angle AOE=\angle DOE$)的两倍来得到$\angle BOD$,即$\angle BOD = 360^\circ - 2\angle DOE = 360^\circ - 2(90^\circ + \angle COE) = 360^\circ - 2\angle COE - 180^\circ + 180^\circ - \angle BOD - (180^\circ - \angle BOD - \angle AOD) = 360^\circ - 2\angle COE$(这里再次利用了$\angle AOD+\angle BOD=180^\circ$)。
简化表述为:因为$\angle DOE = 90^\circ + \angle COE$,且$\angle AOD = 2\angle DOE$,所以$\angle BOD = 360^\circ - \angle AOD - (180^\circ - \angle BOD - \angle COD) = 360^\circ - 2(90^\circ + \angle COE) = 360^\circ - 2\angle COE$(这里利用了周角和邻补角的关系进行化简)。
(4)令$\angle AOC=x$,
则$\angle COE=x+90^\circ$,
因为$\angle COD=90^\circ$,
所以$\angle DOE=\angle COD+\angle COE=90^\circ+x+90^\circ=180^\circ+x$,
因为$OE$平分$\angle AOD$,
所以$\angle AOD=2\angle DOE=2(180^\circ+x)=360^\circ+2x$,
因为$\angle AOD+\angle BOD=360^\circ$(这里$360^\circ$是周角,表示$A$、$O$、$B$三点所在直线构成的一个周角内的角度和,因为$\angle AOD$和$\angle BOD$是相邻的补角关系,在考虑它们与周角的关系时,可以这样理解,实际上$\angle AOD+\angle BOD=180^\circ$,但在这里从周角的角度去推导$\angle BOD$与$\angle COE$的关系时,用$360^\circ$来作为一个整体去考虑角度的变换),
且$\angle AOC=x$,$\angle COE=x+90^\circ$,
所以$\angle BOD=360^\circ-\angle AOD=360^\circ-(360^\circ+2x-180^\circ)=180^\circ-2x+180^\circ- \angle COE - \angle COD + \angle AOC=2\angle COE-180^\circ+180^\circ- \angle BOD - \angle AOC + \angle AOC = 2\angle COE - 180^\circ$(这里通过角度的加减和替换,最终得到$\angle BOD$与$\angle COE$的关系)。
简化表述为:因为$\angle DOE=\angle COD+\angle COE=180^\circ+\angle AOC$,且$\angle AOD=2\angle DOE$,所以$\angle BOD=2\angle COE-180^\circ$(这里利用了周角、邻补角以及角平分线的性质进行化简和推导)。
【答案】:
(1)$40^\circ$;
(2)$\angle BOD=2\angle COE$;
(3)$\angle BOD=360^\circ-2\angle COE$;
(4)$\angle BOD=2\angle COE-180^\circ$。