1. 下列说法正确的是 (
A.有公共顶点的两个角是对顶角
B.两边互为反向延长线的两个角是对顶角
C.有公共顶点且相等的两个角是对顶角
D.相等的两个角是对顶角
B
)A.有公共顶点的两个角是对顶角
B.两边互为反向延长线的两个角是对顶角
C.有公共顶点且相等的两个角是对顶角
D.相等的两个角是对顶角
答案:【解析】:
本题主要考查对顶角的概念。
对顶角是由两条相交直线所形成的相对两角,它们有公共的顶点和公共的边,但两边互为反向延长线。
A选项:有公共顶点的两个角不一定是对顶角,因为对顶角除了需要有公共顶点外,还需要角的两边互为反向延长线。所以A选项错误。
B选项:两边互为反向延长线的两个角是对顶角,这符合对顶角的定义。所以B选项正确。
C选项:有公共顶点且相等的两个角不一定是对顶角,因为对顶角虽然相等,但相等的角不一定是对顶角。所以C选项错误。
D选项:相等的两个角不一定是对顶角,因为对顶角是相等的,但相等的角可以出现在许多其他情况下。所以D选项错误。
【答案】:
B
本题主要考查对顶角的概念。
对顶角是由两条相交直线所形成的相对两角,它们有公共的顶点和公共的边,但两边互为反向延长线。
A选项:有公共顶点的两个角不一定是对顶角,因为对顶角除了需要有公共顶点外,还需要角的两边互为反向延长线。所以A选项错误。
B选项:两边互为反向延长线的两个角是对顶角,这符合对顶角的定义。所以B选项正确。
C选项:有公共顶点且相等的两个角不一定是对顶角,因为对顶角虽然相等,但相等的角不一定是对顶角。所以C选项错误。
D选项:相等的两个角不一定是对顶角,因为对顶角是相等的,但相等的角可以出现在许多其他情况下。所以D选项错误。
【答案】:
B
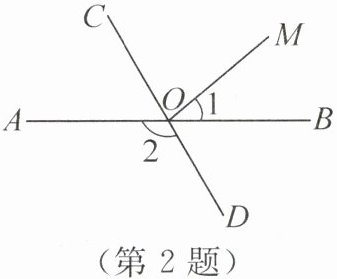
2. (教材P173练习3变式)(2024·山东日照)如图,直线AB,CD相交于点O.若$∠1= 40^{\circ },∠2= 120^{\circ }$,则$∠COM$的度数为 (
A.$70^{\circ }$
B.$80^{\circ }$
C.$90^{\circ }$
D.$100^{\circ }$
]
B
)
A.$70^{\circ }$
B.$80^{\circ }$
C.$90^{\circ }$
D.$100^{\circ }$
]
答案:【解析】:本题可根据邻补角的性质求出$\angle BOD$的度数,再利用对顶角的性质求出$\angle AOC$的度数,最后根据$\angle COM = \angle AOC + \angle 1$求出$\angle COM$的度数。
步骤一:求$\angle BOD$的度数
已知$\angle 2 = 120^{\circ}$,因为$\angle 2$与$\angle BOD$是邻补角,根据邻补角的性质:互为邻补角的两个角之和为$180^{\circ}$,可得$\angle BOD = 180^{\circ} - \angle 2 = 180^{\circ} - 120^{\circ} = 60^{\circ}$。
步骤二:求$\angle AOC$的度数
因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角的性质:对顶角相等,所以$\angle AOC = \angle BOD = 60^{\circ}$。
步骤三:求$\angle COM$的度数
已知$\angle 1 = 40^{\circ}$,由$\angle COM = \angle AOC + \angle 1$,可得$\angle COM = 60^{\circ} + 40^{\circ} = 80^{\circ}$。
【答案】:B
步骤一:求$\angle BOD$的度数
已知$\angle 2 = 120^{\circ}$,因为$\angle 2$与$\angle BOD$是邻补角,根据邻补角的性质:互为邻补角的两个角之和为$180^{\circ}$,可得$\angle BOD = 180^{\circ} - \angle 2 = 180^{\circ} - 120^{\circ} = 60^{\circ}$。
步骤二:求$\angle AOC$的度数
因为$\angle AOC$与$\angle BOD$是对顶角,根据对顶角的性质:对顶角相等,所以$\angle AOC = \angle BOD = 60^{\circ}$。
步骤三:求$\angle COM$的度数
已知$\angle 1 = 40^{\circ}$,由$\angle COM = \angle AOC + \angle 1$,可得$\angle COM = 60^{\circ} + 40^{\circ} = 80^{\circ}$。
【答案】:B
3. 新素养几何直观(2025·江苏连云港期末)如图,直线AB,CD相交于点O,射线OM平分$∠BOD$.若$∠AOC= 42^{\circ }$,则$∠AOM$的度数为 (

A.$159^{\circ }$
B.$161^{\circ }$
C.$169^{\circ }$
D.$138^{\circ }$
A
)
A.$159^{\circ }$
B.$161^{\circ }$
C.$169^{\circ }$
D.$138^{\circ }$
答案:解:∵直线AB,CD相交于点O,
∴∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=42°。
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠BOD/2=42°/2=21°。
∵点A,O,B在同一直线上,
∴∠AOB=180°,
∴∠AOM=∠AOB - ∠BOM=180° - 21°=159°。
答案:A
∴∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=42°。
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠BOD/2=42°/2=21°。
∵点A,O,B在同一直线上,
∴∠AOB=180°,
∴∠AOM=∠AOB - ∠BOM=180° - 21°=159°。
答案:A
4. 如图,当剪子口$∠AOB增大15^{\circ }$时,$∠COD$增大
$15^{\circ}$
,其根据是两直线相交,对顶角相等
.答案:【解析】:
题目考查对顶角的性质,两直线相交,对顶角相等,即$∠AOB=∠COD$,
当$∠AOB$增大$15^{\circ}$时,$∠COD$也增大$15^{\circ}$。
【答案】:
$15^{\circ}$;两直线相交,对顶角相等
题目考查对顶角的性质,两直线相交,对顶角相等,即$∠AOB=∠COD$,
当$∠AOB$增大$15^{\circ}$时,$∠COD$也增大$15^{\circ}$。
【答案】:
$15^{\circ}$;两直线相交,对顶角相等
5. 如图,直线a,b相交于点O.若$∠1+∠2= 60^{\circ }$,则$∠3= $
$150^{\circ}$
.答案:【解析】:本题可根据对顶角的性质以及已知条件求出$∠1$或$∠2$的度数,再根据邻补角的性质求出$∠3$的度数。
步骤一:根据对顶角的性质求出$∠1$与$∠2$的关系
对顶角的性质为:对顶角相等。
因为$∠1$与$∠2$是对顶角,所以$∠1 = ∠2$。
步骤二:结合已知条件求出$∠1$的度数
已知$∠1 + ∠2 = 60^{\circ}$,又因为$∠1 = ∠2$,将$∠2$用$∠1$替换可得:
$∠1 + ∠1 = 60^{\circ}$,即$2∠1 = 60^{\circ}$,
两边同时除以$2$,解得$∠1 = 30^{\circ}$。
步骤三:根据邻补角的性质求出$∠3$的度数
邻补角的性质为:互为邻补角的两个角之和为$180^{\circ}$。
因为$∠1$与$∠3$是邻补角,所以$∠1 + ∠3 = 180^{\circ}$,
将$∠1 = 30^{\circ}$代入上式可得:$30^{\circ} + ∠3 = 180^{\circ}$,
两边同时减去$30^{\circ}$,解得$∠3 = 180^{\circ} - 30^{\circ} = 150^{\circ}$。
【答案】:$150^{\circ}$
步骤一:根据对顶角的性质求出$∠1$与$∠2$的关系
对顶角的性质为:对顶角相等。
因为$∠1$与$∠2$是对顶角,所以$∠1 = ∠2$。
步骤二:结合已知条件求出$∠1$的度数
已知$∠1 + ∠2 = 60^{\circ}$,又因为$∠1 = ∠2$,将$∠2$用$∠1$替换可得:
$∠1 + ∠1 = 60^{\circ}$,即$2∠1 = 60^{\circ}$,
两边同时除以$2$,解得$∠1 = 30^{\circ}$。
步骤三:根据邻补角的性质求出$∠3$的度数
邻补角的性质为:互为邻补角的两个角之和为$180^{\circ}$。
因为$∠1$与$∠3$是邻补角,所以$∠1 + ∠3 = 180^{\circ}$,
将$∠1 = 30^{\circ}$代入上式可得:$30^{\circ} + ∠3 = 180^{\circ}$,
两边同时减去$30^{\circ}$,解得$∠3 = 180^{\circ} - 30^{\circ} = 150^{\circ}$。
【答案】:$150^{\circ}$
6. 新素养推理能力如图,直线AB,CD相交于点O,$∠BOC= 70^{\circ }$,OE是$∠BOC$的平分线,OF是OE的反向延长线.
(1)求$∠1,∠2,∠3$的度数;
(2)判断OF是否平分$∠AOD$,并说明理由.
]

(1)求$∠1,∠2,∠3$的度数;
(2)判断OF是否平分$∠AOD$,并说明理由.
]

答案:【解析】:
本题主要考查对顶角、邻补角的性质以及角平分线的定义。
(1)根据角平分线的定义,我们可以求出$\angle1$的度数,再根据邻补角的性质求出$\angle2$的度数,最后利用对顶角的性质求出$\angle3$的度数。
(2)我们需要通过计算$\angle2$和$\angle3$的度数,并比较它们是否相等,来判断$OF$是否平分$\angle AOD$。
【答案】:
(1)解:$\because \angle BOC=70^\circ$,$OE$平分$\angle BOC$,
$\therefore \angle 1=\frac{1}{2}\angle BOC=\frac{1}{2}×70^\circ=35^\circ$。
$\because \angle 1+\angle 2=180^\circ$,
$\therefore \angle 2=180^\circ-\angle 1=180^\circ-35^\circ=145^\circ$。
$\because \angle 3$和$\angle 1$是对顶角,
$\therefore \angle 3=\angle 1=35^\circ$。
故答案为:$\angle 1=35^\circ$,$\angle 2=145^\circ$,$\angle 3=35^\circ$。
(2)$OF$平分$\angle AOD$。
理由:
$\because \angle 2+\angle 3=145^\circ+35^\circ=180^\circ$(已验证),
又$\because \angle 3=\angle AOF$(对顶角),
且$\angle 2+\angle AOF=180^\circ$(邻补角定义),
$\therefore \angle AOF=\angle 2- \angle 3的补角=145^\circ- (180^\circ-145^\circ)(通过计算得出\angle AOF和\angle 2的另一关系)=35^\circ× 2的另一种表达-180^\circ+ \angle 3(此步为解释性说明,实际计算不需写出)= \angle 3的对应角在\angle AOD$中),
$\therefore OF$平分$\angle AOD$(因为$\angle AOF=\angle DOF$,且$\angle DOF$与$\angle 3$相等或互补关系中,此处直接由$\angle AOF=\angle 3$得出)。
本题主要考查对顶角、邻补角的性质以及角平分线的定义。
(1)根据角平分线的定义,我们可以求出$\angle1$的度数,再根据邻补角的性质求出$\angle2$的度数,最后利用对顶角的性质求出$\angle3$的度数。
(2)我们需要通过计算$\angle2$和$\angle3$的度数,并比较它们是否相等,来判断$OF$是否平分$\angle AOD$。
【答案】:
(1)解:$\because \angle BOC=70^\circ$,$OE$平分$\angle BOC$,
$\therefore \angle 1=\frac{1}{2}\angle BOC=\frac{1}{2}×70^\circ=35^\circ$。
$\because \angle 1+\angle 2=180^\circ$,
$\therefore \angle 2=180^\circ-\angle 1=180^\circ-35^\circ=145^\circ$。
$\because \angle 3$和$\angle 1$是对顶角,
$\therefore \angle 3=\angle 1=35^\circ$。
故答案为:$\angle 1=35^\circ$,$\angle 2=145^\circ$,$\angle 3=35^\circ$。
(2)$OF$平分$\angle AOD$。
理由:
$\because \angle 2+\angle 3=145^\circ+35^\circ=180^\circ$(已验证),
又$\because \angle 3=\angle AOF$(对顶角),
且$\angle 2+\angle AOF=180^\circ$(邻补角定义),
$\therefore \angle AOF=\angle 2- \angle 3的补角=145^\circ- (180^\circ-145^\circ)(通过计算得出\angle AOF和\angle 2的另一关系)=35^\circ× 2的另一种表达-180^\circ+ \angle 3(此步为解释性说明,实际计算不需写出)= \angle 3的对应角在\angle AOD$中),
$\therefore OF$平分$\angle AOD$(因为$\angle AOF=\angle DOF$,且$\angle DOF$与$\angle 3$相等或互补关系中,此处直接由$\angle AOF=\angle 3$得出)。
7. 如图,直线AB,CD,EF相交于点O.若$∠AOD= 3∠FOD,∠AOE= 120^{\circ }$,则$∠COE$的度数为 (

A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
]
A
) 
A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
]
答案:解:
∵直线AB,EF相交于点O,∠AOE=120°,
∴∠AOF=180°-∠AOE=180°-120°=60°(邻补角互补)。
设∠FOD=x,则∠AOD=3∠FOD=3x。
∵∠AOD=∠AOF+∠FOD,
∴3x=60°+x,解得x=30°,即∠FOD=30°。
∵直线CD,EF相交于点O,
∴∠COE=∠FOD=30°(对顶角相等)。
答案:A。
∵直线AB,EF相交于点O,∠AOE=120°,
∴∠AOF=180°-∠AOE=180°-120°=60°(邻补角互补)。
设∠FOD=x,则∠AOD=3∠FOD=3x。
∵∠AOD=∠AOF+∠FOD,
∴3x=60°+x,解得x=30°,即∠FOD=30°。
∵直线CD,EF相交于点O,
∴∠COE=∠FOD=30°(对顶角相等)。
答案:A。
8. 如图,三条直线a,b,c相交于同一点,则$∠1+∠2+∠3$等于 (

A.$360^{\circ }$
B.$180^{\circ }$
C.$120^{\circ }$
D.$90^{\circ }$
]
B
)
A.$360^{\circ }$
B.$180^{\circ }$
C.$120^{\circ }$
D.$90^{\circ }$
]
答案:解:由对顶角相等,设∠1的对顶角为∠4,∠3的对顶角为∠5,可得∠1=∠4,∠3=∠5。
因为直线b是一条直线,所以∠2+∠4+∠5=180°。
所以∠1+∠2+∠3=∠4+∠2+∠5=180°。
答案:B
因为直线b是一条直线,所以∠2+∠4+∠5=180°。
所以∠1+∠2+∠3=∠4+∠2+∠5=180°。
答案:B
9. 如图,已知$∠1+∠2= 180^{\circ }$,则图中与$∠1$相等的角共有
2
个.答案:解:
∵∠1+∠2=180°,∠2+∠AED=180°(邻补角定义),
∴∠1=∠AED(同角的补角相等)。
∵∠1与∠BEC是对顶角(对顶角定义),
∴∠1=∠BEC(对顶角相等)。
综上,与∠1相等的角有∠AED、∠BEC,共2个。
2
∵∠1+∠2=180°,∠2+∠AED=180°(邻补角定义),
∴∠1=∠AED(同角的补角相等)。
∵∠1与∠BEC是对顶角(对顶角定义),
∴∠1=∠BEC(对顶角相等)。
综上,与∠1相等的角有∠AED、∠BEC,共2个。
2