10. 如图,将一张长方形纸片沿线段 BD 折叠,使点 C 落在点$C'$的位置. 若$BC'恰好平分∠ABD$,则$∠ABD= $
$60^{\circ}$
.答案:【解析】:
本题可根据折叠的性质以及角平分线的定义来求解$\angle ABD$的度数。
步骤一:根据折叠的性质得到相关角的关系
由折叠的性质可知,$\triangle BCD$与$\triangle BC'D$关于直线$BD$对称,所以$\angle CBD = \angle C'BD$。
步骤二:根据角平分线的定义得到相关角的关系
因为$BC'$恰好平分$\angle ABD$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,所以$\angle ABC' = \angle C'BD$。
步骤三:找出$\angle ABC$、$\angle CBD$与$\angle ABD$的关系
由于四边形$ABCD$是长方形,所以$\angle ABC = 90^{\circ}$,即$\angle ABC' + \angle C'BD + \angle ABD = 90^{\circ}$。
又因为$\angle ABC' = \angle C'BD$,$\angle CBD = \angle C'BD$,所以$\angle ABC' = \angle C'BD = \angle CBD$。
设$\angle ABC' = \angle C'BD = \angle CBD = x$,则$\angle ABD = 2x$。
步骤四:求解$x$的值,进而得到$\angle ABD$的度数
将$\angle ABC' = x$,$\angle C'BD = x$,$\angle ABD = 2x$代入$\angle ABC' + \angle C'BD + \angle ABD = 90^{\circ}$,可得$x + x + 2x = 90^{\circ}$,即$4x = 90^{\circ}$,解得$x = 30^{\circ}$。
所以$\angle ABD = 2x = 2×30^{\circ} = 60^{\circ}$。
【答案】:
$60^{\circ}$
本题可根据折叠的性质以及角平分线的定义来求解$\angle ABD$的度数。
步骤一:根据折叠的性质得到相关角的关系
由折叠的性质可知,$\triangle BCD$与$\triangle BC'D$关于直线$BD$对称,所以$\angle CBD = \angle C'BD$。
步骤二:根据角平分线的定义得到相关角的关系
因为$BC'$恰好平分$\angle ABD$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,所以$\angle ABC' = \angle C'BD$。
步骤三:找出$\angle ABC$、$\angle CBD$与$\angle ABD$的关系
由于四边形$ABCD$是长方形,所以$\angle ABC = 90^{\circ}$,即$\angle ABC' + \angle C'BD + \angle ABD = 90^{\circ}$。
又因为$\angle ABC' = \angle C'BD$,$\angle CBD = \angle C'BD$,所以$\angle ABC' = \angle C'BD = \angle CBD$。
设$\angle ABC' = \angle C'BD = \angle CBD = x$,则$\angle ABD = 2x$。
步骤四:求解$x$的值,进而得到$\angle ABD$的度数
将$\angle ABC' = x$,$\angle C'BD = x$,$\angle ABD = 2x$代入$\angle ABC' + \angle C'BD + \angle ABD = 90^{\circ}$,可得$x + x + 2x = 90^{\circ}$,即$4x = 90^{\circ}$,解得$x = 30^{\circ}$。
所以$\angle ABD = 2x = 2×30^{\circ} = 60^{\circ}$。
【答案】:
$60^{\circ}$
11. 如图,点 A,O,B 在同一条直线上,$∠AOC= \frac{1}{2}∠BOC+30^{\circ}$,OE 平分$∠BOC$,则$∠BOE= $
$50^{\circ}$
.答案:【解析】:本题可先根据平角的性质得到$\angle AOC$与$\angle BOC$的关系,再结合已知条件$\angle AOC = \frac{1}{2}\angle BOC + 30^{\circ}$求出$\angle BOC$的度数,最后根据角平分线的性质求出$\angle BOE$的度数。
步骤一:根据平角的性质得到$\angle AOC$与$\angle BOC$的关系
因为点$A$,$O$,$B$在同一条直线上,所以$\angle AOB$是平角,平角的度数为$180^{\circ}$,即$\angle AOC + \angle BOC = 180^{\circ}$。
步骤二:结合已知条件求出$\angle BOC$的度数
已知$\angle AOC = \frac{1}{2}\angle BOC + 30^{\circ}$,将其代入$\angle AOC + \angle BOC = 180^{\circ}$中,可得:
$\frac{1}{2}\angle BOC + 30^{\circ} + \angle BOC = 180^{\circ}$
合并同类项可得:$\frac{3}{2}\angle BOC + 30^{\circ} = 180^{\circ}$
移项可得:$\frac{3}{2}\angle BOC = 180^{\circ} - 30^{\circ} = 150^{\circ}$
两边同时除以$\frac{3}{2}$,即$\angle BOC = 150^{\circ} ÷ \frac{3}{2} = 100^{\circ}$。
步骤三:根据角平分线的性质求出$\angle BOE$的度数
因为$OE$平分$\angle BOC$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle BOE = \frac{1}{2}\angle BOC$。
将$\angle BOC = 100^{\circ}$代入可得:$\angle BOE = \frac{1}{2}×100^{\circ} = 50^{\circ}$。
【答案】:$50^{\circ}$
步骤一:根据平角的性质得到$\angle AOC$与$\angle BOC$的关系
因为点$A$,$O$,$B$在同一条直线上,所以$\angle AOB$是平角,平角的度数为$180^{\circ}$,即$\angle AOC + \angle BOC = 180^{\circ}$。
步骤二:结合已知条件求出$\angle BOC$的度数
已知$\angle AOC = \frac{1}{2}\angle BOC + 30^{\circ}$,将其代入$\angle AOC + \angle BOC = 180^{\circ}$中,可得:
$\frac{1}{2}\angle BOC + 30^{\circ} + \angle BOC = 180^{\circ}$
合并同类项可得:$\frac{3}{2}\angle BOC + 30^{\circ} = 180^{\circ}$
移项可得:$\frac{3}{2}\angle BOC = 180^{\circ} - 30^{\circ} = 150^{\circ}$
两边同时除以$\frac{3}{2}$,即$\angle BOC = 150^{\circ} ÷ \frac{3}{2} = 100^{\circ}$。
步骤三:根据角平分线的性质求出$\angle BOE$的度数
因为$OE$平分$\angle BOC$,根据角平分线的性质:角平分线将一个角分成两个相等的角,所以$\angle BOE = \frac{1}{2}\angle BOC$。
将$\angle BOC = 100^{\circ}$代入可得:$\angle BOE = \frac{1}{2}×100^{\circ} = 50^{\circ}$。
【答案】:$50^{\circ}$
12. (2025·江苏淮安期末)如图,$∠AOB= 60^{\circ}$,OC 是$∠AOB$的平分线,$OC_{1}是∠AOC$的平分线,$OC_{2}是∠AOC_{1}$的平分线,…,$OC_{n}是∠AOC_{n-1}$的平分线($n≥2$,且 n 为整数),则$∠AOC_{n}= $
$\frac{60^{\circ}}{2^{n + 1}}$
.答案:【解析】:本题可根据角平分线的性质,逐步求出$\angle AOC_{1}$、$\angle AOC_{2}$等的度数,进而找出$\angle AOC_{n}$的度数规律。
步骤一:求出$\angle AOC$的度数
已知$OC$是$\angle AOB$的平分线,且$\angle AOB = 60^{\circ}$,根据角平分线的性质:角平分线将一个角分成两个相等的角,可得:
$\angle AOC=\frac{1}{2}\angle AOB=\frac{1}{2}×60^{\circ}=30^{\circ}$
步骤二:求出$\angle AOC_{1}$的度数
因为$OC_{1}$是$\angle AOC$的平分线,由角平分线的性质可得:
$\angle AOC_{1}=\frac{1}{2}\angle AOC=\frac{1}{2}×30^{\circ}=15^{\circ}$
步骤三:求出$\angle AOC_{2}$的度数
由于$OC_{2}$是$\angle AOC_{1}$的平分线,同理可得:
$\angle AOC_{2}=\frac{1}{2}\angle AOC_{1}=\frac{1}{2}×15^{\circ}=7.5^{\circ}$
步骤四:找出$\angle AOC_{n}$的度数规律
通过前面的计算可知:
$\angle AOC = 30^{\circ}=\frac{60^{\circ}}{2^{1}}$
$\angle AOC_{1} = 15^{\circ}=\frac{60^{\circ}}{2^{2}}$
$\angle AOC_{2} = 7.5^{\circ}=\frac{60^{\circ}}{2^{3}}$
以此类推,可得出$\angle AOC_{n}=\frac{60^{\circ}}{2^{n + 1}}=\frac{60^{\circ}}{2^{n+1}}$($n\geq2$,且$n$为整数)。
【答案】:$\frac{60^{\circ}}{2^{n + 1}}$
步骤一:求出$\angle AOC$的度数
已知$OC$是$\angle AOB$的平分线,且$\angle AOB = 60^{\circ}$,根据角平分线的性质:角平分线将一个角分成两个相等的角,可得:
$\angle AOC=\frac{1}{2}\angle AOB=\frac{1}{2}×60^{\circ}=30^{\circ}$
步骤二:求出$\angle AOC_{1}$的度数
因为$OC_{1}$是$\angle AOC$的平分线,由角平分线的性质可得:
$\angle AOC_{1}=\frac{1}{2}\angle AOC=\frac{1}{2}×30^{\circ}=15^{\circ}$
步骤三:求出$\angle AOC_{2}$的度数
由于$OC_{2}$是$\angle AOC_{1}$的平分线,同理可得:
$\angle AOC_{2}=\frac{1}{2}\angle AOC_{1}=\frac{1}{2}×15^{\circ}=7.5^{\circ}$
步骤四:找出$\angle AOC_{n}$的度数规律
通过前面的计算可知:
$\angle AOC = 30^{\circ}=\frac{60^{\circ}}{2^{1}}$
$\angle AOC_{1} = 15^{\circ}=\frac{60^{\circ}}{2^{2}}$
$\angle AOC_{2} = 7.5^{\circ}=\frac{60^{\circ}}{2^{3}}$
以此类推,可得出$\angle AOC_{n}=\frac{60^{\circ}}{2^{n + 1}}=\frac{60^{\circ}}{2^{n+1}}$($n\geq2$,且$n$为整数)。
【答案】:$\frac{60^{\circ}}{2^{n + 1}}$
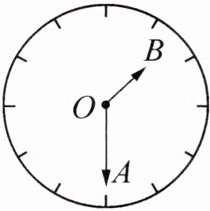
13. 如图,钟表上显示的时间是 1 时 30 分.
(1) 此时时针与分针的夹角为多少度?
(2) 设此时时针与分针的交点为 O,时针为 OB,分针为 OA,过点 O 引一条射线 OC,使$∠BOC= 25^{\circ}$. 若 OM 平分$∠AOC$,ON 平分$∠BOC$,求$∠MON$的度数.
(1) 此时时针与分针的夹角为多少度?
(2) 设此时时针与分针的交点为 O,时针为 OB,分针为 OA,过点 O 引一条射线 OC,使$∠BOC= 25^{\circ}$. 若 OM 平分$∠AOC$,ON 平分$∠BOC$,求$∠MON$的度数.

答案:(1) 解:钟面一圈为$360^{\circ}$,共12个大格,每个大格为$360^{\circ}÷12 = 30^{\circ}$。1时30分,分针指向6,走了6个大格,分针与12点方向夹角为$6×30^{\circ}=180^{\circ}$;时针1小时走1个大格即$30^{\circ}$,30分钟走$30^{\circ}×0.5 = 15^{\circ}$,1时30分时针与12点方向夹角为$1×30^{\circ}+15^{\circ}=45^{\circ}$。所以时针与分针夹角为$180^{\circ}-45^{\circ}=135^{\circ}$。
(2) 解:情况一:OC在∠AOB内部。
因为OM平分∠AOC,ON平分∠BOC,所以∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC。∠MON=∠MOC+∠NOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}×135^{\circ}=67.5^{\circ}$。
情况二:OC在∠AOB外部。
∠MON=∠MOC - ∠NOC=$\frac{1}{2}$∠AOC - $\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC - ∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}×135^{\circ}=67.5^{\circ}$。
综上,∠MON=67.5°。
(2) 解:情况一:OC在∠AOB内部。
因为OM平分∠AOC,ON平分∠BOC,所以∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC。∠MON=∠MOC+∠NOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}×135^{\circ}=67.5^{\circ}$。
情况二:OC在∠AOB外部。
∠MON=∠MOC - ∠NOC=$\frac{1}{2}$∠AOC - $\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC - ∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}×135^{\circ}=67.5^{\circ}$。
综上,∠MON=67.5°。
14. 亮点原创 我们定义:若两个角度数差的绝对值等于$60^{\circ}$,则称这两个角互为“给力角”. 如:$∠1= 160^{\circ},∠2= 100^{\circ}$,$|∠1-∠2|= 60^{\circ}$,则$∠1和∠2$互为“给力角”. 如图,已知$∠MON= 120^{\circ}$,射线 OA 平分$∠MON$,$∠BOC在∠MON$的内部. 若$∠BOC= 60^{\circ},∠AOB≠∠AOC$,则图中互为“给力角”的角共有
6
对.答案:解:
∵∠MON=120°,OA平分∠MON,
∴∠MOA=∠AON=60°。
设∠AOB=x,∠AOC=y,
∵∠BOC=60°,∠AOB≠∠AOC,
∴x+y=60°且x≠y,x>0,y>0。
互为“给力角”的角:
1. ∠MON与∠MOA:|120°-60°|=60°;
2. ∠MON与∠AON:|120°-60°|=60°;
3. ∠MON与∠BOC:|120°-60°|=60°;
4. ∠MOA与∠BOC:|60°-60°|=60°;
5. ∠AON与∠BOC:|60°-60°|=60°;
6. ∠MOB与∠AOC:∠MOB=∠MOA+∠AOB=60°+x,∠AOC=y=60°-x,|(60°+x)-(60°-x)|=|2x|=60°(x=30°时成立,但x≠y=30°,故排除);
7. ∠MOB与∠CON:∠CON=∠AON-∠AOC=60°-y=60°-(60°-x)=x,|∠MOB-∠CON|=|60°+x -x|=60°;
8. ∠AOB与∠CON:∠CON=x,|∠AOB-∠CON|=|x-x|=0°(不成立);
9. ∠AOB与∠MOC:∠MOC=∠MOA+∠AOC=60°+y=120°-x,|∠MOC-∠AOB|=|120°-x -x|=|120°-2x|=60°(x=30°时成立,排除);
10. ∠COB与∠MOA:同3;
11. ∠COB与∠AON:同4;
12. ∠AOC与∠BOM:同6(排除);
有效对: 1,2,3,4,5,7共6对。
答案:6
∵∠MON=120°,OA平分∠MON,
∴∠MOA=∠AON=60°。
设∠AOB=x,∠AOC=y,
∵∠BOC=60°,∠AOB≠∠AOC,
∴x+y=60°且x≠y,x>0,y>0。
互为“给力角”的角:
1. ∠MON与∠MOA:|120°-60°|=60°;
2. ∠MON与∠AON:|120°-60°|=60°;
3. ∠MON与∠BOC:|120°-60°|=60°;
4. ∠MOA与∠BOC:|60°-60°|=60°;
5. ∠AON与∠BOC:|60°-60°|=60°;
6. ∠MOB与∠AOC:∠MOB=∠MOA+∠AOB=60°+x,∠AOC=y=60°-x,|(60°+x)-(60°-x)|=|2x|=60°(x=30°时成立,但x≠y=30°,故排除);
7. ∠MOB与∠CON:∠CON=∠AON-∠AOC=60°-y=60°-(60°-x)=x,|∠MOB-∠CON|=|60°+x -x|=60°;
8. ∠AOB与∠CON:∠CON=x,|∠AOB-∠CON|=|x-x|=0°(不成立);
9. ∠AOB与∠MOC:∠MOC=∠MOA+∠AOC=60°+y=120°-x,|∠MOC-∠AOB|=|120°-x -x|=|120°-2x|=60°(x=30°时成立,排除);
10. ∠COB与∠MOA:同3;
11. ∠COB与∠AON:同4;
12. ∠AOC与∠BOM:同6(排除);
有效对: 1,2,3,4,5,7共6对。
答案:6
15. 如图①,O 为直线 AB 上一点,过点 O 画射线 OC,$∠AOC= 30^{\circ}$,将一块直角三角板($∠M= 30^{\circ}$)的直角顶点放在点 O 处,一边 ON 在射线 OA 上,另一边 OM 在直线 AB 的上方.
(1) 将图①中的三角板绕点 O 以每秒$3^{\circ}$的速度按顺时针方向旋转一周,如图②,则经过多长时间,OM 平分$∠BOC$?
(2) 在(1)的条件下,若三角板在转动的同时,射线 OC 也绕点 O 以每秒$6^{\circ}$的速度按顺时针方向旋转一周,如图③,则经过多长时间,OC 平分$∠MON$?
(3) 在(2)的条件下,经过多长时间,OC 平分$∠BOM$?

(1) 将图①中的三角板绕点 O 以每秒$3^{\circ}$的速度按顺时针方向旋转一周,如图②,则经过多长时间,OM 平分$∠BOC$?
(2) 在(1)的条件下,若三角板在转动的同时,射线 OC 也绕点 O 以每秒$6^{\circ}$的速度按顺时针方向旋转一周,如图③,则经过多长时间,OC 平分$∠MON$?
(3) 在(2)的条件下,经过多长时间,OC 平分$∠BOM$?

答案:(1) 解:设经过 $ t $ 秒,OM 平分 $ \angle BOC $。
初始 $ \angle AOC = 30^\circ $,则 $ \angle BOC = 180^\circ - 30^\circ = 150^\circ $。
三角板顺时针旋转,$ \angle AON = 3t^\circ $,$ \angle MON = 90^\circ $,
$ \angle AOM = \angle AON + \angle MON = 3t^\circ + 90^\circ $,
$ \angle BOM = 180^\circ - \angle AOM = 90^\circ - 3t^\circ $。
OM 平分 $ \angle BOC $,则 $ \angle BOM = \frac{1}{2} \angle BOC = 75^\circ $,
$ 90 - 3t = 75 $,解得 $ t = 5 $。
(2) 解:设经过 $ t $ 秒,OC 平分 $ \angle MON $。
三角板旋转:$ \angle AON = 3t^\circ $,$ \angle AOM = 3t^\circ + 90^\circ $,$ \angle MON = 90^\circ $。
OC 旋转:初始 $ \angle AOC = 30^\circ $,$ t $ 秒后 $ \angle AOC' = 30^\circ + 6t^\circ $(OC'为旋转后位置)。
OC 平分 $ \angle MON $,则 $ \angle MOC = \angle NOC = 45^\circ $。
分两种情况:
① $ \angle AOC' - \angle AON = 45^\circ $,即 $ 30 + 6t - 3t = 45 $,解得 $ t = 5 $;
② $ \angle AON - \angle AOC' = 45^\circ $(OC 旋转超过 ON),即 $ 3t - (30 + 6t) = 45 - 360k $($ k=1 $时),
$ -3t - 30 = -315 $,解得 $ t = 95 $($ t \leq 60 $,舍去)。
综上,$ t = 5 $。
(3) 解:设经过 $ t $ 秒,OC 平分 $ \angle BOM $。
$ \angle BOM = 180^\circ - \angle AOM = 180^\circ - (3t^\circ + 90^\circ) = 90^\circ - 3t^\circ $($ t \leq 30 $时)或 $ 3t^\circ - 270^\circ $($ t > 30 $时)。
OC 旋转后 $ \angle BOC = 180^\circ - (30^\circ + 6t^\circ) = 150^\circ - 6t^\circ $($ t \leq 25 $时)或 $ 6t^\circ - 210^\circ $($ t > 25 $时)。
OC 平分 $ \angle BOM $,则 $ \angle BOC = \frac{1}{2} \angle BOM $。
① $ t \leq 25 $:$ 150 - 6t = \frac{1}{2}(90 - 3t) $,解得 $ t = 14 $;
② $ 25 < t \leq 30 $:$ 6t - 210 = \frac{1}{2}(90 - 3t) $,解得 $ t = \frac{510}{15} = 34 $(舍去);
③ $ t > 30 $:$ 6t - 210 = \frac{1}{2}(3t - 270) $,解得 $ t = 50 $。
综上,$ t = 14 $ 或 $ t = 50 $。
答案:(1) 5 秒;(2) 5 秒;(3) 14 秒或 50 秒。
初始 $ \angle AOC = 30^\circ $,则 $ \angle BOC = 180^\circ - 30^\circ = 150^\circ $。
三角板顺时针旋转,$ \angle AON = 3t^\circ $,$ \angle MON = 90^\circ $,
$ \angle AOM = \angle AON + \angle MON = 3t^\circ + 90^\circ $,
$ \angle BOM = 180^\circ - \angle AOM = 90^\circ - 3t^\circ $。
OM 平分 $ \angle BOC $,则 $ \angle BOM = \frac{1}{2} \angle BOC = 75^\circ $,
$ 90 - 3t = 75 $,解得 $ t = 5 $。
(2) 解:设经过 $ t $ 秒,OC 平分 $ \angle MON $。
三角板旋转:$ \angle AON = 3t^\circ $,$ \angle AOM = 3t^\circ + 90^\circ $,$ \angle MON = 90^\circ $。
OC 旋转:初始 $ \angle AOC = 30^\circ $,$ t $ 秒后 $ \angle AOC' = 30^\circ + 6t^\circ $(OC'为旋转后位置)。
OC 平分 $ \angle MON $,则 $ \angle MOC = \angle NOC = 45^\circ $。
分两种情况:
① $ \angle AOC' - \angle AON = 45^\circ $,即 $ 30 + 6t - 3t = 45 $,解得 $ t = 5 $;
② $ \angle AON - \angle AOC' = 45^\circ $(OC 旋转超过 ON),即 $ 3t - (30 + 6t) = 45 - 360k $($ k=1 $时),
$ -3t - 30 = -315 $,解得 $ t = 95 $($ t \leq 60 $,舍去)。
综上,$ t = 5 $。
(3) 解:设经过 $ t $ 秒,OC 平分 $ \angle BOM $。
$ \angle BOM = 180^\circ - \angle AOM = 180^\circ - (3t^\circ + 90^\circ) = 90^\circ - 3t^\circ $($ t \leq 30 $时)或 $ 3t^\circ - 270^\circ $($ t > 30 $时)。
OC 旋转后 $ \angle BOC = 180^\circ - (30^\circ + 6t^\circ) = 150^\circ - 6t^\circ $($ t \leq 25 $时)或 $ 6t^\circ - 210^\circ $($ t > 25 $时)。
OC 平分 $ \angle BOM $,则 $ \angle BOC = \frac{1}{2} \angle BOM $。
① $ t \leq 25 $:$ 150 - 6t = \frac{1}{2}(90 - 3t) $,解得 $ t = 14 $;
② $ 25 < t \leq 30 $:$ 6t - 210 = \frac{1}{2}(90 - 3t) $,解得 $ t = \frac{510}{15} = 34 $(舍去);
③ $ t > 30 $:$ 6t - 210 = \frac{1}{2}(3t - 270) $,解得 $ t = 50 $。
综上,$ t = 14 $ 或 $ t = 50 $。
答案:(1) 5 秒;(2) 5 秒;(3) 14 秒或 50 秒。