1. 下列度数的角中,利用一副直角三角板不能画出的是 (
A.$105^{\circ}$
B.$75^{\circ}$
C.$130^{\circ}$
D.$15^{\circ}$
C
)A.$105^{\circ}$
B.$75^{\circ}$
C.$130^{\circ}$
D.$15^{\circ}$
答案:【解析】:
本题主要考察的是对直角三角板角度的理解以及角度的组合与计算。
直角三角板一般有两种,一种的角度为$30^{\circ}$、$60^{\circ}$和$90^{\circ}$,另一种的角度为$45^{\circ}$和$90^{\circ}$。
我们需要判断给定的选项中,哪些角度可以通过这两种三角板的角度组合来画出。
A. $105^{\circ}$:可以由$45^{\circ}$和$60^{\circ}$组合得到,即$45^{\circ} + 60^{\circ} = 105^{\circ}$,所以A选项是可以画出的。
B. $75^{\circ}$:可以由$30^{\circ}$和$45^{\circ}$组合得到,即$30^{\circ} + 45^{\circ} = 75^{\circ}$,所以B选项是可以画出的。
C. $130^{\circ}$:这个角度不能通过直角三角板上的任何角度组合来得到,所以C选项是不能画出的。
D. $15^{\circ}$:可以由$45^{\circ}$减去$30^{\circ}$得到,即$45^{\circ} - 30^{\circ} = 15^{\circ}$,或者利用$60^{\circ}$和$45^{\circ}$的差的一半,即$\frac{60^{\circ}-45^{\circ}}{2} = 7.5^{\circ}$的两倍,但更直接的是$45^{\circ}$和$30^{\circ}$的差,所以D选项是可以画出的。
综上所述,不能利用一副直角三角板画出的角度是$130^{\circ}$。
【答案】:
C
本题主要考察的是对直角三角板角度的理解以及角度的组合与计算。
直角三角板一般有两种,一种的角度为$30^{\circ}$、$60^{\circ}$和$90^{\circ}$,另一种的角度为$45^{\circ}$和$90^{\circ}$。
我们需要判断给定的选项中,哪些角度可以通过这两种三角板的角度组合来画出。
A. $105^{\circ}$:可以由$45^{\circ}$和$60^{\circ}$组合得到,即$45^{\circ} + 60^{\circ} = 105^{\circ}$,所以A选项是可以画出的。
B. $75^{\circ}$:可以由$30^{\circ}$和$45^{\circ}$组合得到,即$30^{\circ} + 45^{\circ} = 75^{\circ}$,所以B选项是可以画出的。
C. $130^{\circ}$:这个角度不能通过直角三角板上的任何角度组合来得到,所以C选项是不能画出的。
D. $15^{\circ}$:可以由$45^{\circ}$减去$30^{\circ}$得到,即$45^{\circ} - 30^{\circ} = 15^{\circ}$,或者利用$60^{\circ}$和$45^{\circ}$的差的一半,即$\frac{60^{\circ}-45^{\circ}}{2} = 7.5^{\circ}$的两倍,但更直接的是$45^{\circ}$和$30^{\circ}$的差,所以D选项是可以画出的。
综上所述,不能利用一副直角三角板画出的角度是$130^{\circ}$。
【答案】:
C
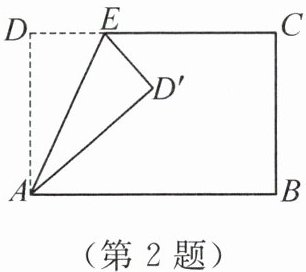
2. 将长方形纸片 ABCD 沿 AE 折叠,得到如图所示的图形. 若$∠CED'= 50^{\circ}$,则$∠AED$的度数为 (
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$
答案:【解析】:
本题考查的是通过折叠变换的性质以及平角的定义来求解$∠AED$的度数,涉及到角的大小比较知识点。
已知长方形纸片$ABCD$沿$AE$折叠,根据折叠的性质可知,折叠前后对应角相等,所以$∠AED$与$∠AED'$是对应角,那么$∠AED = ∠AED'$。
又因为$∠DED'$是一个平角,平角的度数为$180^{\circ}$,即$∠DED' = 180^{\circ}$。
而$∠DED' = ∠AED + ∠AED' + ∠CED'$,且$∠AED = ∠AED'$,所以$∠AED + ∠AED' = 180^{\circ} - ∠CED'$。
已知$∠CED' = 50^{\circ}$,将其代入上式可得$∠AED + ∠AED' = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
因为$∠AED = ∠AED'$,所以$∠AED = \frac{1}{2}×130^{\circ} = 65^{\circ}$。
【答案】:C。
本题考查的是通过折叠变换的性质以及平角的定义来求解$∠AED$的度数,涉及到角的大小比较知识点。
已知长方形纸片$ABCD$沿$AE$折叠,根据折叠的性质可知,折叠前后对应角相等,所以$∠AED$与$∠AED'$是对应角,那么$∠AED = ∠AED'$。
又因为$∠DED'$是一个平角,平角的度数为$180^{\circ}$,即$∠DED' = 180^{\circ}$。
而$∠DED' = ∠AED + ∠AED' + ∠CED'$,且$∠AED = ∠AED'$,所以$∠AED + ∠AED' = 180^{\circ} - ∠CED'$。
已知$∠CED' = 50^{\circ}$,将其代入上式可得$∠AED + ∠AED' = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
因为$∠AED = ∠AED'$,所以$∠AED = \frac{1}{2}×130^{\circ} = 65^{\circ}$。
【答案】:C。
3. (2025·江苏盐城期末)如图,$∠AOB= 130^{\circ}$,OC 是$∠AOB$内部任意一条射线,OD,OE 分别是$∠AOC,∠BOC$的平分线,下列叙述正确的是 (

A.$∠DOE$的度数不能确定
B.$∠AOD= \frac{1}{2}∠EOC$
C.$∠AOD+∠BOE= 65^{\circ}$
D.$∠BOE= 2∠COD$
C
)
A.$∠DOE$的度数不能确定
B.$∠AOD= \frac{1}{2}∠EOC$
C.$∠AOD+∠BOE= 65^{\circ}$
D.$∠BOE= 2∠COD$
答案:【解析】:本题可根据角平分线的性质,分别表示出$\angle AOD$、$\angle BOE$、$\angle DOE$等角与$\angle AOC$、$\angle BOC$的关系,再结合已知条件$\angle AOB = 130^{\circ}$,$\angle AOB=\angle AOC + \angle BOC$来逐一分析选项。
选项A:判断$\angle DOE$的度数是否能确定
因为$OD$是$\angle AOC$的平分线,所以$\angle AOD = \angle DOC=\frac{1}{2}\angle AOC$;
因为$OE$是$\angle BOC$的平分线,所以$\angle BOE = \angle EOC=\frac{1}{2}\angle BOC$。
则$\angle DOE = \angle DOC + \angle EOC=\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC + \angle BOC)$。
又因为$\angle AOB=\angle AOC + \angle BOC = 130^{\circ}$,所以$\angle DOE=\frac{1}{2}×130^{\circ}= 65^{\circ}$,度数可以确定,故选项A错误。
选项B:判断$\angle AOD$与$\frac{1}{2}\angle EOC$的关系
由上述分析可知$\angle AOD = \frac{1}{2}\angle AOC$,$\angle EOC=\frac{1}{2}\angle BOC$,$\angle AOD$与$\frac{1}{2}\angle EOC$没有直接的倍数关系,故选项B错误。
选项C:判断$\angle AOD + \angle BOE$的度数
因为$\angle AOD = \frac{1}{2}\angle AOC$,$\angle BOE = \frac{1}{2}\angle BOC$,所以$\angle AOD + \angle BOE=\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC + \angle BOC)$。
又因为$\angle AOB=\angle AOC + \angle BOC = 130^{\circ}$,所以$\angle AOD + \angle BOE=\frac{1}{2}×130^{\circ}= 65^{\circ}$,故选项C正确。
选项D:判断$\angle BOE$与$2\angle COD$的关系
因为$\angle BOE = \frac{1}{2}\angle BOC$,$\angle COD = \frac{1}{2}\angle AOC$,所以$2\angle COD = \angle AOC$,$\angle BOE$与$2\angle COD$没有直接的倍数关系,故选项D错误。
【答案】:C
选项A:判断$\angle DOE$的度数是否能确定
因为$OD$是$\angle AOC$的平分线,所以$\angle AOD = \angle DOC=\frac{1}{2}\angle AOC$;
因为$OE$是$\angle BOC$的平分线,所以$\angle BOE = \angle EOC=\frac{1}{2}\angle BOC$。
则$\angle DOE = \angle DOC + \angle EOC=\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC + \angle BOC)$。
又因为$\angle AOB=\angle AOC + \angle BOC = 130^{\circ}$,所以$\angle DOE=\frac{1}{2}×130^{\circ}= 65^{\circ}$,度数可以确定,故选项A错误。
选项B:判断$\angle AOD$与$\frac{1}{2}\angle EOC$的关系
由上述分析可知$\angle AOD = \frac{1}{2}\angle AOC$,$\angle EOC=\frac{1}{2}\angle BOC$,$\angle AOD$与$\frac{1}{2}\angle EOC$没有直接的倍数关系,故选项B错误。
选项C:判断$\angle AOD + \angle BOE$的度数
因为$\angle AOD = \frac{1}{2}\angle AOC$,$\angle BOE = \frac{1}{2}\angle BOC$,所以$\angle AOD + \angle BOE=\frac{1}{2}\angle AOC + \frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC + \angle BOC)$。
又因为$\angle AOB=\angle AOC + \angle BOC = 130^{\circ}$,所以$\angle AOD + \angle BOE=\frac{1}{2}×130^{\circ}= 65^{\circ}$,故选项C正确。
选项D:判断$\angle BOE$与$2\angle COD$的关系
因为$\angle BOE = \frac{1}{2}\angle BOC$,$\angle COD = \frac{1}{2}\angle AOC$,所以$2\angle COD = \angle AOC$,$\angle BOE$与$2\angle COD$没有直接的倍数关系,故选项D错误。
【答案】:C
4. (教材 P169 练习 2 变式)如图,AB 与 CD 相交于点 O,OE 是$∠AOC$的平分线,且 OC 恰好平分$∠EOB$,则$∠AOD$的度数为
60°
.答案:解:设∠AOE = x。
∵OE是∠AOC的平分线,
∴∠EOC = ∠AOE = x。
∵OC平分∠EOB,
∴∠COB = ∠EOC = x。
∵点A,O,B在同一直线上,
∴∠AOE + ∠EOC + ∠COB = 180°,
即x + x + x = 180°,解得x = 60°。
∴∠AOC = ∠AOE + ∠EOC = 60° + 60° = 120°。
∵∠AOD与∠AOC互为邻补角,
∴∠AOD = 180° - ∠AOC = 180° - 120° = 60°。
60°
∵OE是∠AOC的平分线,
∴∠EOC = ∠AOE = x。
∵OC平分∠EOB,
∴∠COB = ∠EOC = x。
∵点A,O,B在同一直线上,
∴∠AOE + ∠EOC + ∠COB = 180°,
即x + x + x = 180°,解得x = 60°。
∴∠AOC = ∠AOE + ∠EOC = 60° + 60° = 120°。
∵∠AOD与∠AOC互为邻补角,
∴∠AOD = 180° - ∠AOC = 180° - 120° = 60°。
60°
5. 如图,射线 OC,OD 是锐角$∠AOB$的三等分线. 若图中所有锐角的度数之和为$150^{\circ}$,则$∠AOC= $
15°
.答案:解:设∠AOC = x°,因为OC,OD是∠AOB的三等分线,所以∠COD = ∠DOB = x°,∠AOD = 2x°,∠COB = 2x°,∠AOB = 3x°。
图中所有锐角为:∠AOC,∠COD,∠DOB,∠AOD,∠COB,∠AOB,共6个。
它们的度数之和为:x + x + x + 2x + 2x + 3x = 10x。
已知所有锐角的度数之和为150°,则10x = 150,解得x = 15。
所以∠AOC = 15°。
答案:15°
图中所有锐角为:∠AOC,∠COD,∠DOB,∠AOD,∠COB,∠AOB,共6个。
它们的度数之和为:x + x + x + 2x + 2x + 3x = 10x。
已知所有锐角的度数之和为150°,则10x = 150,解得x = 15。
所以∠AOC = 15°。
答案:15°
6. 如图,P 为直线 AB 上一点,PC,PD 为$∠APB$的三等分线,PM,PN 分别为$∠BPC,∠APD$的平分线,求$∠MPN$的度数.


答案:解:
∵P为直线AB上一点,
∴∠APB=180°。
∵PC,PD为∠APB的三等分线,
∴∠APD=∠DPC=∠CPB=180°÷3=60°。
∵PN平分∠APD,
∴∠APN=∠NPD=∠APD÷2=60°÷2=30°。
∵PM平分∠BPC,
∴∠CPM=∠MPB=∠BPC÷2=60°÷2=30°。
∵∠MPN=∠NPD+∠DPC+∠CPM,
∴∠MPN=30°+60°+30°=120°。
答:∠MPN的度数为120°。
∵P为直线AB上一点,
∴∠APB=180°。
∵PC,PD为∠APB的三等分线,
∴∠APD=∠DPC=∠CPB=180°÷3=60°。
∵PN平分∠APD,
∴∠APN=∠NPD=∠APD÷2=60°÷2=30°。
∵PM平分∠BPC,
∴∠CPM=∠MPB=∠BPC÷2=60°÷2=30°。
∵∠MPN=∠NPD+∠DPC+∠CPM,
∴∠MPN=30°+60°+30°=120°。
答:∠MPN的度数为120°。
7. 如图,OE 平分$∠AOB$,射线 OC 在$∠AOE$内,$∠BOC= 2∠AOC$. 若$∠AOB= 114^{\circ}$,则$∠COE$的度数为 (
A.$18^{\circ}$
B.$19^{\circ}$
C.$20^{\circ}$
D.$21^{\circ}$
B
)A.$18^{\circ}$
B.$19^{\circ}$
C.$20^{\circ}$
D.$21^{\circ}$
答案:【解析】:本题可先根据角平分线的性质求出$\angle AOE$的度数,再结合$\angle BOC = 2\angle AOC$以及$\angle AOB$的度数求出$\angle AOC$的度数,最后根据$\angle COE=\angle AOE - \angle AOC$求出$\angle COE$的度数。
步骤一:求出$\angle AOE$的度数
已知$OE$平分$\angle AOB$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,可得$\angle AOE=\frac{1}{2}\angle AOB$。
因为$\angle AOB = 114^{\circ}$,所以$\angle AOE=\frac{1}{2}×114^{\circ}= 57^{\circ}$。
步骤二:求出$\angle AOC$的度数
因为$\angle AOB=\angle AOC+\angle BOC$,且$\angle BOC = 2\angle AOC$,所以$\angle AOB=\angle AOC + 2\angle AOC = 3\angle AOC$。
则$\angle AOC=\frac{1}{3}\angle AOB$,将$\angle AOB = 114^{\circ}$代入可得:$\angle AOC=\frac{1}{3}×114^{\circ}= 38^{\circ}$。
步骤三:求出$\angle COE$的度数
由$\angle COE=\angle AOE - \angle AOC$,将$\angle AOE = 57^{\circ}$,$\angle AOC = 38^{\circ}$代入可得:
$\angle COE = 57^{\circ}- 38^{\circ}= 19^{\circ}$
【答案】:B
步骤一:求出$\angle AOE$的度数
已知$OE$平分$\angle AOB$,根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,可得$\angle AOE=\frac{1}{2}\angle AOB$。
因为$\angle AOB = 114^{\circ}$,所以$\angle AOE=\frac{1}{2}×114^{\circ}= 57^{\circ}$。
步骤二:求出$\angle AOC$的度数
因为$\angle AOB=\angle AOC+\angle BOC$,且$\angle BOC = 2\angle AOC$,所以$\angle AOB=\angle AOC + 2\angle AOC = 3\angle AOC$。
则$\angle AOC=\frac{1}{3}\angle AOB$,将$\angle AOB = 114^{\circ}$代入可得:$\angle AOC=\frac{1}{3}×114^{\circ}= 38^{\circ}$。
步骤三:求出$\angle COE$的度数
由$\angle COE=\angle AOE - \angle AOC$,将$\angle AOE = 57^{\circ}$,$\angle AOC = 38^{\circ}$代入可得:
$\angle COE = 57^{\circ}- 38^{\circ}= 19^{\circ}$
【答案】:B
8. 如图,已知$∠AOC= 90^{\circ},∠COB= α$,OD 平分$∠AOB$,则$∠COD$的度数为 (

A.$\frac{α}{2}$
B.$45^{\circ}-\frac{α}{2}$
C.$45^{\circ}-α$
D.$90^{\circ}-α$
B
) 
A.$\frac{α}{2}$
B.$45^{\circ}-\frac{α}{2}$
C.$45^{\circ}-α$
D.$90^{\circ}-α$
答案:解:由图可知,∠AOB = ∠AOC + ∠COB = 90° + α
∵OD平分∠AOB
∴∠AOD = 1/2∠AOB = 1/2(90° + α) = 45° + α/2
∵∠AOC = 90°
∴∠COD = ∠AOC - ∠AOD = 90° - (45° + α/2) = 45° - α/2
答案:B
∵OD平分∠AOB
∴∠AOD = 1/2∠AOB = 1/2(90° + α) = 45° + α/2
∵∠AOC = 90°
∴∠COD = ∠AOC - ∠AOD = 90° - (45° + α/2) = 45° - α/2
答案:B
9. 已知$∠AOB= 60^{\circ}$,射线 OC 平分$∠AOB$. 若以 OC 为一边画$∠COP= 15^{\circ}$,则$∠BOP$的度数为 (
A.$15^{\circ}$
B.$45^{\circ}$
C.$15^{\circ}或30^{\circ}$
D.$15^{\circ}或45^{\circ}$
D
)A.$15^{\circ}$
B.$45^{\circ}$
C.$15^{\circ}或30^{\circ}$
D.$15^{\circ}或45^{\circ}$
答案:【解析】:
本题主要考查了角的大小比较和角的平分线的性质。
首先,根据题目条件,知道$\angle AOB = 60^\circ$,并且射线$OC$平分$\angle AOB$。
根据角的平分线的性质,我们可以得出$\angle BOC = \frac{1}{2} \angle AOB = 30^\circ$。
接下来,题目说以$OC$为一边画$\angle COP = 15^\circ$。
这里有两种可能的情况:
当$\angle COP$的一边与$\angle BOC$的一边在同一条直线上时(即$\angle COP$在$\angle BOC$的内部),
$\angle BOP = \angle BOC - \angle COP = 30^\circ - 15^\circ = 15^\circ$。
当$\angle COP$的一边与$\angle BOC$的另一边不在同一条直线上时(即$\angle COP$在$\angle BOC$的外部),
$\angle BOP = \angle BOC + \angle COP = 30^\circ + 15^\circ = 45^\circ$。
综合以上两种情况,$\angle BOP$的度数可以是$15^\circ$或$45^\circ$。
【答案】:
D. $15^\circ$或$45^\circ$。
本题主要考查了角的大小比较和角的平分线的性质。
首先,根据题目条件,知道$\angle AOB = 60^\circ$,并且射线$OC$平分$\angle AOB$。
根据角的平分线的性质,我们可以得出$\angle BOC = \frac{1}{2} \angle AOB = 30^\circ$。
接下来,题目说以$OC$为一边画$\angle COP = 15^\circ$。
这里有两种可能的情况:
当$\angle COP$的一边与$\angle BOC$的一边在同一条直线上时(即$\angle COP$在$\angle BOC$的内部),
$\angle BOP = \angle BOC - \angle COP = 30^\circ - 15^\circ = 15^\circ$。
当$\angle COP$的一边与$\angle BOC$的另一边不在同一条直线上时(即$\angle COP$在$\angle BOC$的外部),
$\angle BOP = \angle BOC + \angle COP = 30^\circ + 15^\circ = 45^\circ$。
综合以上两种情况,$\angle BOP$的度数可以是$15^\circ$或$45^\circ$。
【答案】:
D. $15^\circ$或$45^\circ$。