13. 如图,已知$∠AOB与∠BOC$互补,$∠AOD= ∠BOD$,OE 在$∠BOC$的内部.若$∠BOE= \frac {1}{2}∠COE$,$∠DOE= 72^{\circ }$,则$∠COE$的度数是____
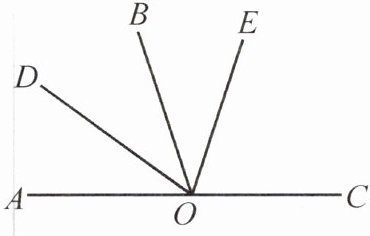
72°
。
答案:解:设∠COE=x°,则∠BOE=1/2x°,∠BOC=∠BOE+∠COE=3/2x°。
∵∠AOB与∠BOC互补,
∴∠AOB=180°-∠BOC=180°-3/2x°。
∵∠AOD=∠BOD,
∴∠BOD=1/2∠AOB=1/2(180°-3/2x°)=90°-3/4x°。
∵∠DOE=∠BOD+∠BOE=72°,
∴90°-3/4x°+1/2x°=72°,
解得x=72。
∠COE=72°。
∵∠AOB与∠BOC互补,
∴∠AOB=180°-∠BOC=180°-3/2x°。
∵∠AOD=∠BOD,
∴∠BOD=1/2∠AOB=1/2(180°-3/2x°)=90°-3/4x°。
∵∠DOE=∠BOD+∠BOE=72°,
∴90°-3/4x°+1/2x°=72°,
解得x=72。
∠COE=72°。
14. 新素养 推理能力 如图,A,O,E 三点在同一条直线上,$∠AOB= \frac {1}{2}∠AOC$,$∠AOB与∠DOE$互余,则$∠COD与∠DOE$之间有什么数量关系?请说明理由.


答案:解:∠COD=∠DOE。理由如下:
设∠AOB=x,则∠AOC=2x,∠BOC=∠AOC-∠AOB=2x-x=x。
因为∠AOB与∠DOE互余,所以∠AOB+∠DOE=90°,即∠DOE=90°-x。
因为A,O,E三点在同一条直线上,所以∠AOE=180°,即∠AOC+∠COD+∠DOE=180°。
所以2x+∠COD+(90°-x)=180°,解得∠COD=90°-x。
所以∠COD=∠DOE。
设∠AOB=x,则∠AOC=2x,∠BOC=∠AOC-∠AOB=2x-x=x。
因为∠AOB与∠DOE互余,所以∠AOB+∠DOE=90°,即∠DOE=90°-x。
因为A,O,E三点在同一条直线上,所以∠AOE=180°,即∠AOC+∠COD+∠DOE=180°。
所以2x+∠COD+(90°-x)=180°,解得∠COD=90°-x。
所以∠COD=∠DOE。
15. (2025·江苏扬州期末)已知$∠α与∠β$互补,且$∠α>∠β$,给出下列式子:①$90^{\circ }-∠β$;②$∠α-90^{\circ }$;③$180^{\circ }-∠α$;④$\frac {1}{2}(∠α-∠β)$.其中能表示$∠β$的余角的是(
A.①②③④
B.①②④
C.①②③
D.①②
B
)A.①②③④
B.①②④
C.①②③
D.①②
答案:【解析】:
本题主要考察补角和余角的概念及性质。
首先,根据题目条件,$\angle \alpha$ 与 $\angle \beta$ 是互补角,即 $\angle \alpha + \angle \beta = 180^{\circ}$。
余角的定义是两个角的和为 $90^{\circ}$。
接下来,逐一检验给出的四个式子:
① $90^{\circ} - \angle \beta$:
这个式子直接表示了 $\angle \beta$ 的余角,因为 $90^{\circ} - \angle \beta + \angle \beta = 90^{\circ}$。
② $\angle \alpha - 90^{\circ}$:
由于 $\angle \alpha + \angle \beta = 180^{\circ}$,
则 $\angle \alpha = 180^{\circ} - \angle \beta$。
所以 $\angle \alpha - 90^{\circ} = 90^{\circ} - \angle \beta$,
这也表示了 $\angle \beta$ 的余角。
③ $180^{\circ} - \angle \alpha$:
这个式子实际上表示的是 $\angle \beta$(因为 $\angle \alpha + \angle \beta = 180^{\circ}$),
并不是 $\angle \beta$ 的余角。
④ $\frac{1}{2}(\angle \alpha - \angle \beta)$:
由于 $\angle \alpha + \angle \beta = 180^{\circ}$,
则 $\angle \alpha - \angle \beta = 180^{\circ} - 2\angle \beta$。
所以 $\frac{1}{2}(\angle \alpha - \angle \beta) = 90^{\circ} - \angle \beta$,
这也表示了 $\angle \beta$ 的余角。
综上所述,能表示 $\angle \beta$ 的余角的是 ①、②和④。
【答案】:B
本题主要考察补角和余角的概念及性质。
首先,根据题目条件,$\angle \alpha$ 与 $\angle \beta$ 是互补角,即 $\angle \alpha + \angle \beta = 180^{\circ}$。
余角的定义是两个角的和为 $90^{\circ}$。
接下来,逐一检验给出的四个式子:
① $90^{\circ} - \angle \beta$:
这个式子直接表示了 $\angle \beta$ 的余角,因为 $90^{\circ} - \angle \beta + \angle \beta = 90^{\circ}$。
② $\angle \alpha - 90^{\circ}$:
由于 $\angle \alpha + \angle \beta = 180^{\circ}$,
则 $\angle \alpha = 180^{\circ} - \angle \beta$。
所以 $\angle \alpha - 90^{\circ} = 90^{\circ} - \angle \beta$,
这也表示了 $\angle \beta$ 的余角。
③ $180^{\circ} - \angle \alpha$:
这个式子实际上表示的是 $\angle \beta$(因为 $\angle \alpha + \angle \beta = 180^{\circ}$),
并不是 $\angle \beta$ 的余角。
④ $\frac{1}{2}(\angle \alpha - \angle \beta)$:
由于 $\angle \alpha + \angle \beta = 180^{\circ}$,
则 $\angle \alpha - \angle \beta = 180^{\circ} - 2\angle \beta$。
所以 $\frac{1}{2}(\angle \alpha - \angle \beta) = 90^{\circ} - \angle \beta$,
这也表示了 $\angle \beta$ 的余角。
综上所述,能表示 $\angle \beta$ 的余角的是 ①、②和④。
【答案】:B
16. 如图,已知$∠AOB与∠COD都是∠BOC$的余角,$∠AOE= ∠BOE$,$∠COF= ∠DOF$.若$∠BOC= 50^{\circ }$,求$∠AOD与∠EOF$的度数.


答案:【解析】:本题考查余角性质,对顶角性质,角之间的数量关系。
根据题意,$∠AOB$与$∠COD$都是$∠BOC$的余角,则有$∠AOB=∠COD=90^{\circ}-∠BOC=90^{\circ}-50^{\circ}=40^{\circ}$。
$∠AOD=∠AOB+∠BOC+∠COD=40^{\circ}+50^{\circ}+40^{\circ}=130^{\circ}$。
$∠BOD=∠BOC+∠COD=50^{\circ}+40^{\circ}=90^{\circ}$。
因为$OE$平分$∠AOB$,$OF$平分$∠COD$。
所以$∠AOE=∠BOE=\frac{∠AOB}{2}=\frac{40^{\circ}}{2}=20^{\circ}$,
$∠COF=∠DOF=\frac{∠COD}{2}=\frac{40^{\circ}}{2}=20^{\circ}$。
$∠EOF=∠BOC+∠COF+∠BOE=50^{\circ}+20^{\circ}+20^{\circ}=90^{\circ}$。
【答案】:$∠AOD=130^{\circ}$,$∠EOF=90^{\circ}$。
根据题意,$∠AOB$与$∠COD$都是$∠BOC$的余角,则有$∠AOB=∠COD=90^{\circ}-∠BOC=90^{\circ}-50^{\circ}=40^{\circ}$。
$∠AOD=∠AOB+∠BOC+∠COD=40^{\circ}+50^{\circ}+40^{\circ}=130^{\circ}$。
$∠BOD=∠BOC+∠COD=50^{\circ}+40^{\circ}=90^{\circ}$。
因为$OE$平分$∠AOB$,$OF$平分$∠COD$。
所以$∠AOE=∠BOE=\frac{∠AOB}{2}=\frac{40^{\circ}}{2}=20^{\circ}$,
$∠COF=∠DOF=\frac{∠COD}{2}=\frac{40^{\circ}}{2}=20^{\circ}$。
$∠EOF=∠BOC+∠COF+∠BOE=50^{\circ}+20^{\circ}+20^{\circ}=90^{\circ}$。
【答案】:$∠AOD=130^{\circ}$,$∠EOF=90^{\circ}$。
17. 新趋势 推导探究 将一副直角三角板的直角顶点重合,并按如图所示的方式叠放在一起.
(1)如图①,若$∠BOD= 35^{\circ }$,则$∠AOC= $
(2)如图②,若$∠AOC= 140^{\circ }$,则$∠BOD= $
(3)猜想$∠AOC与∠BOD$之间的数量关系,并结合图①说明理由;
(4)三角板 AOB 不动,将三角板 COD 的边 OD 与边 OA 重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当$∠AOD(0^{\circ }<∠AOD<90^{\circ })$等于多少度时,这两块三角板各有一条边所在的直线形成$90^{\circ }$角?直接写出$∠AOD$度数的所有可能值,不用说明理由.
(1)如图①,若$∠BOD= 35^{\circ }$,则$∠AOC= $
$145^{\circ }$
;若$∠AOC= 135^{\circ }$,则$∠BOD= $$45^{\circ }$
;(2)如图②,若$∠AOC= 140^{\circ }$,则$∠BOD= $
$40^{\circ }$
;(3)猜想$∠AOC与∠BOD$之间的数量关系,并结合图①说明理由;
$\angle AOC + \angle BOD = 180^\circ$,理由:由于$\angle AOB = \angle COD = 90^\circ$,根据角的和的关系,有$\angle AOC + \angle BOD = \angle AOB + \angle COD - \angle BOD + \angle BOD = \angle AOB + \angle COD = 90^\circ + 90^\circ = 180^\circ$。
(4)三角板 AOB 不动,将三角板 COD 的边 OD 与边 OA 重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当$∠AOD(0^{\circ }<∠AOD<90^{\circ })$等于多少度时,这两块三角板各有一条边所在的直线形成$90^{\circ }$角?直接写出$∠AOD$度数的所有可能值,不用说明理由.
$30^\circ$、$45^\circ$、$60^\circ$
答案:【解析】:
本题主要考查了补角、余角的概念以及角度的计算。
(1)对于第一个空,由于$\angle AOB = \angle COD = 90^\circ$,且$\angle BOD = 35^\circ$,
根据角的和的关系,有$\angle AOC = \angle AOB + \angle COD - \angle BOD = 90^\circ + 90^\circ - 35^\circ = 145^\circ$。
对于第二个空,若$\angle AOC = 135^\circ$,
则$\angle BOD = \angle AOB + \angle COD - \angle AOC = 90^\circ + 90^\circ - 135^\circ = 45^\circ$。
(2)若$\angle AOC = 140^\circ$,
则$\angle BOD = \angle AOB + \angle COD - \angle AOC = 90^\circ + 90^\circ - 140^\circ = 40^\circ$。
(3)猜想$\angle AOC$与$\angle BOD$之间的数量关系为$\angle AOC + \angle BOD = 180^\circ$。
理由:由于$\angle AOB = \angle COD = 90^\circ$,
根据角的和的关系,有$\angle AOC + \angle BOD = \angle AOB + \angle COD - \angle BOD + \angle BOD = \angle AOB + \angle COD = 90^\circ + 90^\circ = 180^\circ$。
(4)当$\angle AOD$等于$30^\circ$、$45^\circ$、$60^\circ$时,这两块三角板各有一条边所在的直线形成$90^\circ$角。
【答案】:
(1)$145^\circ$;$45^\circ$
(2)$40^\circ$
(3)$\angle AOC + \angle BOD = 180^\circ$,理由见上述解析
(4)$30^\circ$、$45^\circ$、$60^\circ$
本题主要考查了补角、余角的概念以及角度的计算。
(1)对于第一个空,由于$\angle AOB = \angle COD = 90^\circ$,且$\angle BOD = 35^\circ$,
根据角的和的关系,有$\angle AOC = \angle AOB + \angle COD - \angle BOD = 90^\circ + 90^\circ - 35^\circ = 145^\circ$。
对于第二个空,若$\angle AOC = 135^\circ$,
则$\angle BOD = \angle AOB + \angle COD - \angle AOC = 90^\circ + 90^\circ - 135^\circ = 45^\circ$。
(2)若$\angle AOC = 140^\circ$,
则$\angle BOD = \angle AOB + \angle COD - \angle AOC = 90^\circ + 90^\circ - 140^\circ = 40^\circ$。
(3)猜想$\angle AOC$与$\angle BOD$之间的数量关系为$\angle AOC + \angle BOD = 180^\circ$。
理由:由于$\angle AOB = \angle COD = 90^\circ$,
根据角的和的关系,有$\angle AOC + \angle BOD = \angle AOB + \angle COD - \angle BOD + \angle BOD = \angle AOB + \angle COD = 90^\circ + 90^\circ = 180^\circ$。
(4)当$\angle AOD$等于$30^\circ$、$45^\circ$、$60^\circ$时,这两块三角板各有一条边所在的直线形成$90^\circ$角。
【答案】:
(1)$145^\circ$;$45^\circ$
(2)$40^\circ$
(3)$\angle AOC + \angle BOD = 180^\circ$,理由见上述解析
(4)$30^\circ$、$45^\circ$、$60^\circ$