1. (教材 P166 练习 1 变式)(2024·甘肃兰州)若$∠A= 80^{\circ }$,则$∠A$的补角是(
A.$100^{\circ }$
B.$80^{\circ }$
C.$40^{\circ }$
D.$10^{\circ }$
A
)A.$100^{\circ }$
B.$80^{\circ }$
C.$40^{\circ }$
D.$10^{\circ }$
答案:【解析】:
题目考查了补角的概念及计算。
根据补角的定义,两个角的度数和为$180^{\circ}$,则这两个角互为补角。
已知$∠A = 80^{\circ}$,要求$∠A$的补角,即求一个角,使其与$∠A$的度数和为$180^{\circ}$。
设$∠A$的补角为$x$,则有:
$x + 80^{\circ} = 180^{\circ}$,
解得:
$x = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
【答案】:
A. $100^{\circ}$。
题目考查了补角的概念及计算。
根据补角的定义,两个角的度数和为$180^{\circ}$,则这两个角互为补角。
已知$∠A = 80^{\circ}$,要求$∠A$的补角,即求一个角,使其与$∠A$的度数和为$180^{\circ}$。
设$∠A$的补角为$x$,则有:
$x + 80^{\circ} = 180^{\circ}$,
解得:
$x = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
【答案】:
A. $100^{\circ}$。
2. 下列说法正确的是(
A.互补的两个角一定是一个锐角和一个钝角
B.在三角形中,互余的两个角一定都是锐角
C.平角就是一条直线
D.若$∠A+∠B+∠C= 180^{\circ }$,则$∠A$,$∠B$,$∠C$三角互补
B
)A.互补的两个角一定是一个锐角和一个钝角
B.在三角形中,互余的两个角一定都是锐角
C.平角就是一条直线
D.若$∠A+∠B+∠C= 180^{\circ }$,则$∠A$,$∠B$,$∠C$三角互补
答案:【解析】:
本题主要考查了补角、余角的概念以及三角形内角和定理。
A选项:互补的两个角之和为$180^{\circ}$,但并不意味着它们一定是一个锐角和一个钝角,它们也有可能都是直角,即两个$90^{\circ}$的角,所以A选项错误。
B选项:在三角形中,如果两个角互余,即它们的和为$90^{\circ}$,那么这两个角都必然是锐角,因为钝角和直角的和都大于$90^{\circ}$,所以B选项正确。
C选项:平角是一个角,其度数为$180^{\circ}$,而不是一条直线。直线是两端无限延伸的,没有度数,所以C选项错误。
D选项:若$\angle A + \angle B + \angle C = 180^{\circ}$,这只能说明这三个角是三角形的三个内角,根据三角形内角和定理,三角形的三个内角之和为$180^{\circ}$。而互补是指两个角的和为$180^{\circ}$,所以不能说$\angle A$,$\angle B$,$\angle C$三角互补,D选项错误。
【答案】:
B
本题主要考查了补角、余角的概念以及三角形内角和定理。
A选项:互补的两个角之和为$180^{\circ}$,但并不意味着它们一定是一个锐角和一个钝角,它们也有可能都是直角,即两个$90^{\circ}$的角,所以A选项错误。
B选项:在三角形中,如果两个角互余,即它们的和为$90^{\circ}$,那么这两个角都必然是锐角,因为钝角和直角的和都大于$90^{\circ}$,所以B选项正确。
C选项:平角是一个角,其度数为$180^{\circ}$,而不是一条直线。直线是两端无限延伸的,没有度数,所以C选项错误。
D选项:若$\angle A + \angle B + \angle C = 180^{\circ}$,这只能说明这三个角是三角形的三个内角,根据三角形内角和定理,三角形的三个内角之和为$180^{\circ}$。而互补是指两个角的和为$180^{\circ}$,所以不能说$\angle A$,$\angle B$,$\angle C$三角互补,D选项错误。
【答案】:
B
3. 已知$∠α$是锐角,$∠α与∠β$互补,$∠α与∠γ$互余,则$∠β-∠γ$等于(
A.$45^{\circ }$
B.$60^{\circ }$
C.$90^{\circ }$
D.$180^{\circ }$
C
)A.$45^{\circ }$
B.$60^{\circ }$
C.$90^{\circ }$
D.$180^{\circ }$
答案:【解析】:
题目考查了补角和余角的概念及其性质。
根据补角的定义,如果两个角的和是$180^{\circ}$,则这两个角互为补角。
根据余角的定义,如果两个角的和是$90^{\circ}$,则这两个角互为余角。
由题意知$∠α$与$∠β$互补,所以有:
$∠α + ∠β = 180^{\circ}$,
从上式可以解出$∠β$为:
$∠β = 180^{\circ} - ∠α$,
同样地,由题意知$∠α$与$∠γ$互余,所以有:
$∠α + ∠γ = 90^{\circ}$,
从上式可以解出$∠γ$为:
$∠γ = 90^{\circ} - ∠α$,
接下来,我们需要求$∠β - ∠γ$,代入前面得到的$∠β$和$∠γ$的表达式,得:
$∠β - ∠γ = (180^{\circ} - ∠α) - (90^{\circ} - ∠α) = 90^{\circ}$。
【答案】:
C. $90^{\circ}$。
题目考查了补角和余角的概念及其性质。
根据补角的定义,如果两个角的和是$180^{\circ}$,则这两个角互为补角。
根据余角的定义,如果两个角的和是$90^{\circ}$,则这两个角互为余角。
由题意知$∠α$与$∠β$互补,所以有:
$∠α + ∠β = 180^{\circ}$,
从上式可以解出$∠β$为:
$∠β = 180^{\circ} - ∠α$,
同样地,由题意知$∠α$与$∠γ$互余,所以有:
$∠α + ∠γ = 90^{\circ}$,
从上式可以解出$∠γ$为:
$∠γ = 90^{\circ} - ∠α$,
接下来,我们需要求$∠β - ∠γ$,代入前面得到的$∠β$和$∠γ$的表达式,得:
$∠β - ∠γ = (180^{\circ} - ∠α) - (90^{\circ} - ∠α) = 90^{\circ}$。
【答案】:
C. $90^{\circ}$。
4. (1)已知$∠α=60^{\circ }$,则$∠α$的余角的大小是
(2)已知$∠A的补角为60^{\circ }$,则$∠A$的度数为
$30^{\circ}$
;(2)已知$∠A的补角为60^{\circ }$,则$∠A$的度数为
$120^{\circ}$
。答案:(1)解:因为互为余角的两个角的和为$90^{\circ}$,$\angle\alpha = 60^{\circ}$,所以$\angle\alpha$的余角为$90^{\circ}-60^{\circ}=30^{\circ}$。
(2)解:因为互为补角的两个角的和为$180^{\circ}$,$\angle A$的补角为$60^{\circ}$,所以$\angle A = 180^{\circ}-60^{\circ}=120^{\circ}$。
(1)$30^{\circ}$;(2)$120^{\circ}$
(2)解:因为互为补角的两个角的和为$180^{\circ}$,$\angle A$的补角为$60^{\circ}$,所以$\angle A = 180^{\circ}-60^{\circ}=120^{\circ}$。
(1)$30^{\circ}$;(2)$120^{\circ}$
5. 如图,将两个正方形的一个顶点重合放置.若$∠AOD= 40^{\circ }$,则$∠COB= $
$140^{\circ }$
。答案:【解析】:本题考查补角余角的知识点。
题目给出了两个正方形的一个顶点重合,且$\angle AOD= 40^{\circ }$。
需要求$\angle COB$。
正方形的每个内角都是$90^{\circ }$。
$\angle AOD$和$\angle COB$分别与两个相邻的角$\angle AOC$和$\angle BOD$构成补角关系,即$\angle AOC+\angle AOD= 90^{\circ }$,$\angle BOD+\angle AOD= 90^{\circ }$。
由于$\angle AOD= 40^{\circ }$,
所以$\angle AOC= 90^{\circ }-40^{\circ }= 50^{\circ }$,
$\angle BOD= 90^{\circ }-40^{\circ }= 50^{\circ }$。
因此$\angle COB= \angle AOC+\angle AOD+\angle BOD= 50^{\circ }+40^{\circ }+50^{\circ }= 140^{\circ }$(舍去)或者$\angle COB=360^{\circ}-90^{\circ}-90^{\circ}-40^{\circ}=140^{\circ}$。
【答案】:$140^{\circ }$。
题目给出了两个正方形的一个顶点重合,且$\angle AOD= 40^{\circ }$。
需要求$\angle COB$。
正方形的每个内角都是$90^{\circ }$。
$\angle AOD$和$\angle COB$分别与两个相邻的角$\angle AOC$和$\angle BOD$构成补角关系,即$\angle AOC+\angle AOD= 90^{\circ }$,$\angle BOD+\angle AOD= 90^{\circ }$。
由于$\angle AOD= 40^{\circ }$,
所以$\angle AOC= 90^{\circ }-40^{\circ }= 50^{\circ }$,
$\angle BOD= 90^{\circ }-40^{\circ }= 50^{\circ }$。
因此$\angle COB= \angle AOC+\angle AOD+\angle BOD= 50^{\circ }+40^{\circ }+50^{\circ }= 140^{\circ }$(舍去)或者$\angle COB=360^{\circ}-90^{\circ}-90^{\circ}-40^{\circ}=140^{\circ}$。
【答案】:$140^{\circ }$。
6. 若两个角的补角互余,则这两个角的和为
$270^{\circ}$
。答案:解:设这两个角分别为$\alpha$和$\beta$。
因为互为补角的两个角之和为$180^{\circ}$,所以$\alpha$的补角为$180^{\circ}-\alpha$,$\beta$的补角为$180^{\circ}-\beta$。
已知这两个角的补角互余,即两个补角之和为$90^{\circ}$,可得:
$(180^{\circ}-\alpha)+(180^{\circ}-\beta)=90^{\circ}$
化简得:$360^{\circ}-(\alpha+\beta)=90^{\circ}$
移项可得:$\alpha+\beta=360^{\circ}-90^{\circ}=270^{\circ}$
故这两个角的和为$270^{\circ}$。
答案:$270^{\circ}$
因为互为补角的两个角之和为$180^{\circ}$,所以$\alpha$的补角为$180^{\circ}-\alpha$,$\beta$的补角为$180^{\circ}-\beta$。
已知这两个角的补角互余,即两个补角之和为$90^{\circ}$,可得:
$(180^{\circ}-\alpha)+(180^{\circ}-\beta)=90^{\circ}$
化简得:$360^{\circ}-(\alpha+\beta)=90^{\circ}$
移项可得:$\alpha+\beta=360^{\circ}-90^{\circ}=270^{\circ}$
故这两个角的和为$270^{\circ}$。
答案:$270^{\circ}$
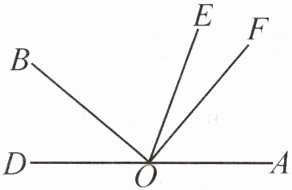
7. 新素养 几何直观 如图,O 为直线 DA 上一点,$∠AOE= ∠BOE$,$∠BOF= 90^{\circ }$。
(1)$∠AOF$的余角是
(2)若$∠EOF= 20^{\circ }$,求$∠AOF$的度数。
(1)$∠AOF$的余角是
∠BOE、∠AOE
,$∠BOD$的补角是∠AOB
;(2)若$∠EOF= 20^{\circ }$,求$∠AOF$的度数。

解:因为∠BOF=90°,∠EOF=20°,所以∠BOE=∠BOF - ∠EOF=90° - 20°=70°。
因为∠AOE=∠BOE,所以∠AOE=70°。
所以∠AOF=∠AOE + ∠EOF=70° + 20°=90°。
因为∠AOE=∠BOE,所以∠AOE=70°。
所以∠AOF=∠AOE + ∠EOF=70° + 20°=90°。
答案:(1)∠BOE、∠AOE;∠AOB
(2)解:因为∠BOF=90°,∠EOF=20°,所以∠BOE=∠BOF - ∠EOF=90° - 20°=70°。
因为∠AOE=∠BOE,所以∠AOE=70°。
所以∠AOF=∠AOE + ∠EOF=70° + 20°=90°。
(2)解:因为∠BOF=90°,∠EOF=20°,所以∠BOE=∠BOF - ∠EOF=90° - 20°=70°。
因为∠AOE=∠BOE,所以∠AOE=70°。
所以∠AOF=∠AOE + ∠EOF=70° + 20°=90°。
8. (2025·江苏镇江期末)给出下列说法:① 锐角的补角一定是钝角;② 一个角的补角一定大于这个角;③ 如果两个角是同一个角的补角,那么这两个角相等;④ 锐角和钝角互补.其中正确的是(
A.①②
B.①③
C.①②③
D.①②③④
B
)A.①②
B.①③
C.①②③
D.①②③④
答案:【解析】:
本题主要考查了补角和余角的概念及性质。
① 锐角的补角一定是钝角:
设锐角为$a$,则$0^\circ < a < 90^\circ$,
其补角为$180^\circ - a$,由于$0 < a < 90$,所以$90 < 180 - a < 180$,即补角为钝角。
所以①正确。
② 一个角的补角一定大于这个角:
考虑$90^\circ$的补角,它也是$90^\circ$,并不大于原角。
所以②错误。
③ 如果两个角是同一个角的补角,那么这两个角相等:
设角$A$的补角为$B$和$C$,则$B = 180^\circ - A$,$C = 180^\circ - A$,所以$B = C$。
所以③正确。
④ 锐角和钝角互补:
锐角小于$90^\circ$,钝角大于$90^\circ$,它们的和不一定为$180^\circ$,所以它们不一定互补。
所以④错误。
综上,正确的选项是B,即①和③。
【答案】:
B
本题主要考查了补角和余角的概念及性质。
① 锐角的补角一定是钝角:
设锐角为$a$,则$0^\circ < a < 90^\circ$,
其补角为$180^\circ - a$,由于$0 < a < 90$,所以$90 < 180 - a < 180$,即补角为钝角。
所以①正确。
② 一个角的补角一定大于这个角:
考虑$90^\circ$的补角,它也是$90^\circ$,并不大于原角。
所以②错误。
③ 如果两个角是同一个角的补角,那么这两个角相等:
设角$A$的补角为$B$和$C$,则$B = 180^\circ - A$,$C = 180^\circ - A$,所以$B = C$。
所以③正确。
④ 锐角和钝角互补:
锐角小于$90^\circ$,钝角大于$90^\circ$,它们的和不一定为$180^\circ$,所以它们不一定互补。
所以④错误。
综上,正确的选项是B,即①和③。
【答案】:
B
9. 如图,点 A,O,B 在同一条直线上.若$∠AOE= ∠DOF$,$∠BOF= ∠DOE$,则图中互余的角共有(
A.5 对
B.4 对
C.3 对
D.2 对
B
)A.5 对
B.4 对
C.3 对
D.2 对
答案:解:设∠AOE=∠DOF=α,∠BOF=∠DOE=β。
∵点A,O,B在同一直线上,
∴∠AOB=180°,即∠AOE+∠DOE+∠DOF+∠BOF=180°,
∴α+β+α+β=180°,2(α+β)=180°,α+β=90°。
∵∠AOE+∠DOE=α+β=90°,∴∠AOE与∠DOE互余;
∵∠AOE+∠BOF=α+β=90°,∴∠AOE与∠BOF互余;
∵∠DOF+∠DOE=α+β=90°,∴∠DOF与∠DOE互余;
∵∠DOF+∠BOF=α+β=90°,∴∠DOF与∠BOF互余。
综上,互余的角共有4对。
答案:B
∵点A,O,B在同一直线上,
∴∠AOB=180°,即∠AOE+∠DOE+∠DOF+∠BOF=180°,
∴α+β+α+β=180°,2(α+β)=180°,α+β=90°。
∵∠AOE+∠DOE=α+β=90°,∴∠AOE与∠DOE互余;
∵∠AOE+∠BOF=α+β=90°,∴∠AOE与∠BOF互余;
∵∠DOF+∠DOE=α+β=90°,∴∠DOF与∠DOE互余;
∵∠DOF+∠BOF=α+β=90°,∴∠DOF与∠BOF互余。
综上,互余的角共有4对。
答案:B
10. 已知$∠α与∠β的度数分别是(2m-67)^{\circ }和(68-m)^{\circ }$,且$∠α与∠β都是∠γ$的补角,则$∠α与∠β$之间的关系是(
A.互余但不相等
B.互补
C.相等但不互余
D.互余且相等
C
)A.互余但不相等
B.互补
C.相等但不互余
D.互余且相等
答案:【解析】:
首先,我们需要明确题目中的关键信息,即$∠α$和$∠β$都是$∠γ$的补角。
根据补角的定义,如果两个角是同一个角的补角,那么这两个角相等。
因此,我们可以直接得出$∠α = ∠β$。
接下来,我们需要判断$∠α$和$∠β$是否互余。
互余的定义是两个角的度数之和为$90^\circ$。
为了验证这一点,我们可以将$∠α$和$∠β$的度数表达式相加,并化简:
$(2m - 67)^\circ + (68 - m)^\circ$
$= 2m^\circ - 67^\circ + 68^\circ - m^\circ$
$= (2m - m)^\circ + (-67 + 68)^\circ$
$= m^\circ + 1^\circ$
由于结果并不等于$90^\circ$,且m为未知数,我们不能确定$m$的具体值,因此我们不能直接断定$∠α$和$∠β$是互余的。
但我们可以根据补角的性质确定它们是相等的。
然而,我们可以利用题目中的选项来进一步判断。
由于我们已经知道$∠α = ∠β$,我们可以考虑它们是否可能互余。
如果$∠α$和$∠β$互余,则它们的度数之和应为$90^\circ$。
将$∠α$和$∠β$的度数表达式相加并设等于$90^\circ$,我们得到:
$(2m - 67)^\circ + (68 - m)^\circ = 90^\circ$
但化简后我们得到$m^\circ + 1^\circ = 90^\circ$,
这是一个矛盾,因为$m$不可能为$89$(否则$∠α$或$∠β$的度数将为负或超过$180^\circ$,这与角的定义矛盾)。
因此,我们可以确定$∠α$和$∠β$不互余。
所以,$∠α$和$∠β$之间的关系是相等但不互余。
【答案】:C. 相等但不互余。
首先,我们需要明确题目中的关键信息,即$∠α$和$∠β$都是$∠γ$的补角。
根据补角的定义,如果两个角是同一个角的补角,那么这两个角相等。
因此,我们可以直接得出$∠α = ∠β$。
接下来,我们需要判断$∠α$和$∠β$是否互余。
互余的定义是两个角的度数之和为$90^\circ$。
为了验证这一点,我们可以将$∠α$和$∠β$的度数表达式相加,并化简:
$(2m - 67)^\circ + (68 - m)^\circ$
$= 2m^\circ - 67^\circ + 68^\circ - m^\circ$
$= (2m - m)^\circ + (-67 + 68)^\circ$
$= m^\circ + 1^\circ$
由于结果并不等于$90^\circ$,且m为未知数,我们不能确定$m$的具体值,因此我们不能直接断定$∠α$和$∠β$是互余的。
但我们可以根据补角的性质确定它们是相等的。
然而,我们可以利用题目中的选项来进一步判断。
由于我们已经知道$∠α = ∠β$,我们可以考虑它们是否可能互余。
如果$∠α$和$∠β$互余,则它们的度数之和应为$90^\circ$。
将$∠α$和$∠β$的度数表达式相加并设等于$90^\circ$,我们得到:
$(2m - 67)^\circ + (68 - m)^\circ = 90^\circ$
但化简后我们得到$m^\circ + 1^\circ = 90^\circ$,
这是一个矛盾,因为$m$不可能为$89$(否则$∠α$或$∠β$的度数将为负或超过$180^\circ$,这与角的定义矛盾)。
因此,我们可以确定$∠α$和$∠β$不互余。
所以,$∠α$和$∠β$之间的关系是相等但不互余。
【答案】:C. 相等但不互余。
11. 若一个角的补角加上$10^{\circ }$后,等于它的余角的 3 倍,则该角的度数为
$40^{\circ}$
。答案:【解析】:
本题主要考查补角和余角的概念以及一元一次方程的建立和求解。
首先,设这个角的度数为$x^{\circ}$。
根据补角的定义,这个角的补角为$180^{\circ} - x^{\circ}$。
根据余角的定义,这个角的余角为$90^{\circ} - x^{\circ}$。
根据题意,补角加上$10^{\circ}$后等于余角的3倍,可以列出方程:
$180^{\circ} - x^{\circ} + 10^{\circ} = 3(90^{\circ} - x^{\circ})$,
解这个方程,得到:
$190^{\circ} - x^{\circ} = 270^{\circ} - 3x^{\circ}$,
$2x^{\circ} = 80^{\circ}$,
$x = 40^{\circ}$,
【答案】:
$40^{\circ}$。
本题主要考查补角和余角的概念以及一元一次方程的建立和求解。
首先,设这个角的度数为$x^{\circ}$。
根据补角的定义,这个角的补角为$180^{\circ} - x^{\circ}$。
根据余角的定义,这个角的余角为$90^{\circ} - x^{\circ}$。
根据题意,补角加上$10^{\circ}$后等于余角的3倍,可以列出方程:
$180^{\circ} - x^{\circ} + 10^{\circ} = 3(90^{\circ} - x^{\circ})$,
解这个方程,得到:
$190^{\circ} - x^{\circ} = 270^{\circ} - 3x^{\circ}$,
$2x^{\circ} = 80^{\circ}$,
$x = 40^{\circ}$,
【答案】:
$40^{\circ}$。
12. 若一个角的余角的 3 倍比它的补角的 2 倍小$120^{\circ }$,则该角的度数为
$30^{\circ}$
。答案:【解析】:
本题主要考查余角和补角的概念及一元一次方程的建立与求解。
设这个角的度数为$x$,则其余角为$90^{\circ} - x$,补角为$180^{\circ} - x$。
根据题意,这个角的余角的3倍比它的补角的2倍小$120^{\circ}$,可以列出方程:
$3(90^{\circ} - x) = 2(180^{\circ} - x) - 120^{\circ}$
展开方程得:
$270^{\circ} - 3x = 360^{\circ} - 2x - 120^{\circ}$
移项并合并同类项:
$-x = 360^{\circ} - 270^{\circ} - 120^{\circ}$
$-x = -30^{\circ}$
解得:
$x = 30^{\circ}$
【答案】:
$30^{\circ}$
本题主要考查余角和补角的概念及一元一次方程的建立与求解。
设这个角的度数为$x$,则其余角为$90^{\circ} - x$,补角为$180^{\circ} - x$。
根据题意,这个角的余角的3倍比它的补角的2倍小$120^{\circ}$,可以列出方程:
$3(90^{\circ} - x) = 2(180^{\circ} - x) - 120^{\circ}$
展开方程得:
$270^{\circ} - 3x = 360^{\circ} - 2x - 120^{\circ}$
移项并合并同类项:
$-x = 360^{\circ} - 270^{\circ} - 120^{\circ}$
$-x = -30^{\circ}$
解得:
$x = 30^{\circ}$
【答案】:
$30^{\circ}$