1. 下列说法正确的是 (
A.一条直线的平行线有且只有一条
B.经过一点有两条直线与已知直线平行
C.过一点有且只有一条直线与已知直线平行
D.过直线外一点有且只有一条直线与已知直线平行
D
)A.一条直线的平行线有且只有一条
B.经过一点有两条直线与已知直线平行
C.过一点有且只有一条直线与已知直线平行
D.过直线外一点有且只有一条直线与已知直线平行
答案:【解析】:
本题主要考察平行线的基本性质与定义。
A选项:根据平行线的定义,一条直线可以有无数条与其平行的直线,因此A选项错误。
B选项:对于平面上的任意一点和一条已知直线,通过这一点只能作出一条与已知直线平行的直线,而非两条,所以B选项错误。
C选项:这个选项没有明确指出这一点是在直线外还是直线上。如果这一点在直线上,那么通过这一点无法作出与该直线平行的另一条直线(因为两直线重合不是平行的定义)。所以C选项的描述不够准确,错误。
D选项:这是平行线的一个基本性质,即通过直线外的一个点,可以作出且仅可以作出一条与该直线平行的直线。所以D选项正确。
【答案】:
D
本题主要考察平行线的基本性质与定义。
A选项:根据平行线的定义,一条直线可以有无数条与其平行的直线,因此A选项错误。
B选项:对于平面上的任意一点和一条已知直线,通过这一点只能作出一条与已知直线平行的直线,而非两条,所以B选项错误。
C选项:这个选项没有明确指出这一点是在直线外还是直线上。如果这一点在直线上,那么通过这一点无法作出与该直线平行的另一条直线(因为两直线重合不是平行的定义)。所以C选项的描述不够准确,错误。
D选项:这是平行线的一个基本性质,即通过直线外的一个点,可以作出且仅可以作出一条与该直线平行的直线。所以D选项正确。
【答案】:
D
2. (2025·江苏苏州期末)如图,在同一平面内,经过直线a外一点O的4条直线中,与直线a相交的直线至少有 (
A.4条
B.3条
C.2条
D.1条
B
)A.4条
B.3条
C.2条
D.1条
答案:【解析】:
根据平行线的定义,经过直线外一点有且只有一条直线与这条直线平行。
由此可以推断,经过直线$a$外一点$O$,如果不与$a$平行的直线,那么它们必然与$a$相交。
在同一平面内,经过直线$a$外一点$O$的4条直线中,最多只能有一条与$a$平行(根据平行公理)。
因此,至少有$4 - 1 = 3$条直线与$a$相交。
这里的关键是理解“至少”的含义,即除了可能存在的与$a$平行的那一条直线外,其余的都与$a$相交。
【答案】:B
根据平行线的定义,经过直线外一点有且只有一条直线与这条直线平行。
由此可以推断,经过直线$a$外一点$O$,如果不与$a$平行的直线,那么它们必然与$a$相交。
在同一平面内,经过直线$a$外一点$O$的4条直线中,最多只能有一条与$a$平行(根据平行公理)。
因此,至少有$4 - 1 = 3$条直线与$a$相交。
这里的关键是理解“至少”的含义,即除了可能存在的与$a$平行的那一条直线外,其余的都与$a$相交。
【答案】:B
3. 观察如图所示的长方体,与棱AB平行的棱的条数为 (
A.4
B.3
C.2
D.1
B
)A.4
B.3
C.2
D.1
答案:【解析】:
题目要求找出与棱$AB$平行的棱的条数,需要了解长方体的结构以及平行线的定义,在同一平面内,不相交的两条直线叫做平行线,长方体中相对的棱互相平行,从图中可以看到,棱$AB$所在的平面有前后面和左右面两个平面,与棱$AB$在同一平面内的棱都与棱$AB$相交,与棱$AB$平行的棱在其相对面上,棱$AB$相对的棱为$CD$,$A'B'$,$C'D'$,这三条棱都与棱$AB$平行。
【答案】:
B。
题目要求找出与棱$AB$平行的棱的条数,需要了解长方体的结构以及平行线的定义,在同一平面内,不相交的两条直线叫做平行线,长方体中相对的棱互相平行,从图中可以看到,棱$AB$所在的平面有前后面和左右面两个平面,与棱$AB$在同一平面内的棱都与棱$AB$相交,与棱$AB$平行的棱在其相对面上,棱$AB$相对的棱为$CD$,$A'B'$,$C'D'$,这三条棱都与棱$AB$平行。
【答案】:
B。
4. 已知a,b是同一平面内的任意两条直线.
(1) 若直线a,b没有公共点,则直线a,b的位置关系是
(2) 若直线a,b有且只有一个公共点,则直线a,b的位置关系是
(1) 若直线a,b没有公共点,则直线a,b的位置关系是
平行
;(2) 若直线a,b有且只有一个公共点,则直线a,b的位置关系是
相交
.答案:【解析】:
本题主要考察平行线和相交线的概念。在同一平面内,如果两条直线没有公共点,则这两条直线是平行的;如果两条直线有且仅有一个公共点,则这两条直线是相交的。
(1) 对于第一部分,题目已给出直线a,b在同一平面内且没有公共点,根据平行线的定义,我们可以直接得出直线a,b的位置关系是平行。
(2) 对于第二部分,题目已给出直线a,b在同一平面内有且仅有一个公共点,根据相交线的定义,我们可以直接得出直线a,b的位置关系是相交。
【答案】:
(1) 平行
(2) 相交
本题主要考察平行线和相交线的概念。在同一平面内,如果两条直线没有公共点,则这两条直线是平行的;如果两条直线有且仅有一个公共点,则这两条直线是相交的。
(1) 对于第一部分,题目已给出直线a,b在同一平面内且没有公共点,根据平行线的定义,我们可以直接得出直线a,b的位置关系是平行。
(2) 对于第二部分,题目已给出直线a,b在同一平面内有且仅有一个公共点,根据相交线的定义,我们可以直接得出直线a,b的位置关系是相交。
【答案】:
(1) 平行
(2) 相交
5. 新素养 几何直观 如图,在同一平面内,有三条直线a,b,c,且$a// b$.如果直线a与c相交于点O,那么直线c与b的位置关系是
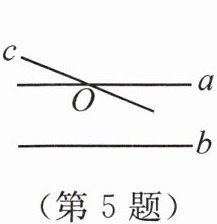
相交
.
答案:【解析】:本题考查平行线的性质。
已知直线a与直线b平行,记作$a// b$。
直线c与直线a在点O处相交。
根据平行线的性质,如果一条直线与平行线中的一条相交,那么它必定与另一条也相交。
所以,直线c与直线b的位置关系是相交。
【答案】:相交
已知直线a与直线b平行,记作$a// b$。
直线c与直线a在点O处相交。
根据平行线的性质,如果一条直线与平行线中的一条相交,那么它必定与另一条也相交。
所以,直线c与直线b的位置关系是相交。
【答案】:相交
6. 如图,$PC// AB,QC// AB$,则点P,C,Q在同一条直线上,理由是
经过直线外一点,有且只有一条直线与这条直线平行
.答案:【解析】:本题主要考查平行线的公理。
根据平行线的公理:平行于同一条直线的两条直线互相平行,以及推论:两条直线都与第三条直线平行,那么这两条直线也互相平行。
在本题中,已知$PC// AB$,$QC// AB$,即$PC$和$QC$都平行于$AB$。
根据上述推论可知$PC$和$QC$是同一条直线,所以点$P$,$C$,$Q$在同一条直线上。
【答案】:经过直线外一点,有且只有一条直线与这条直线平行。
根据平行线的公理:平行于同一条直线的两条直线互相平行,以及推论:两条直线都与第三条直线平行,那么这两条直线也互相平行。
在本题中,已知$PC// AB$,$QC// AB$,即$PC$和$QC$都平行于$AB$。
根据上述推论可知$PC$和$QC$是同一条直线,所以点$P$,$C$,$Q$在同一条直线上。
【答案】:经过直线外一点,有且只有一条直线与这条直线平行。
7. (教材P181活动变式)
(1) 在如图所示的方格纸中找出互相平行的线段,并用符号表示出来;
(2) 过点M画OG的平行线;
(3) 过点N画CD的平行线.

(1) 在如图所示的方格纸中找出互相平行的线段,并用符号表示出来;
(2) 过点M画OG的平行线;
(3) 过点N画CD的平行线.

答案:【解析】:
本题主要考查平行线的判断方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;垂直于同一条直线的两条直线平行,在网格中,通过观察格点位置关系来判断。
(1)观察方格纸,对于线段$AB$和$CD$,可以通过数格点来找出它们之间的关系。
设小方格的边长为$1$,$AB$所在直线的斜率$k_{AB}=\frac{3}{3}=1$,$CD$所在直线的斜率$k_{CD}=\frac{3}{3}=1$,因为$k_{AB}=k_{CD}$,所以$AB// CD$。
同理,$OG$所在直线的斜率$k_{OG}=\frac{1}{2}$,$EF$所在直线的斜率$k_{EF}=\frac{1}{2}$,因为$k_{OG}=k_{EF}$,所以$OG// EF$。
(2)过点$M$画$OG$的平行线,先确定$OG$的斜率$k_{OG}=\frac{1}{2}$,那么过点$M$且斜率为$\frac{1}{2}$的直线就是$OG$的平行线。
(3)过点$N$画$CD$的平行线,$CD$的斜率$k_{CD}=1$,过点$N$且斜率为$1$的直线就是$CD$的平行线。
【答案】:
(1)$AB// CD$,$OG// EF$;
(2)图略;
(3)图略。
本题主要考查平行线的判断方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;垂直于同一条直线的两条直线平行,在网格中,通过观察格点位置关系来判断。
(1)观察方格纸,对于线段$AB$和$CD$,可以通过数格点来找出它们之间的关系。
设小方格的边长为$1$,$AB$所在直线的斜率$k_{AB}=\frac{3}{3}=1$,$CD$所在直线的斜率$k_{CD}=\frac{3}{3}=1$,因为$k_{AB}=k_{CD}$,所以$AB// CD$。
同理,$OG$所在直线的斜率$k_{OG}=\frac{1}{2}$,$EF$所在直线的斜率$k_{EF}=\frac{1}{2}$,因为$k_{OG}=k_{EF}$,所以$OG// EF$。
(2)过点$M$画$OG$的平行线,先确定$OG$的斜率$k_{OG}=\frac{1}{2}$,那么过点$M$且斜率为$\frac{1}{2}$的直线就是$OG$的平行线。
(3)过点$N$画$CD$的平行线,$CD$的斜率$k_{CD}=1$,过点$N$且斜率为$1$的直线就是$CD$的平行线。
【答案】:
(1)$AB// CD$,$OG// EF$;
(2)图略;
(3)图略。
8. 同一平面内有三条互不重合的直线.如果只有两条直线互相平行,那么这三条直线交点的个数为 (
A.0
B.1
C.2
D.3
C
)A.0
B.1
C.2
D.3
答案:解:同一平面内三条互不重合的直线,只有两条互相平行。
因为两条平行线无交点,第三条直线与这两条平行线分别相交,会产生2个交点。
所以交点个数为2。
答案:C
因为两条平行线无交点,第三条直线与这两条平行线分别相交,会产生2个交点。
所以交点个数为2。
答案:C
9. 在同一平面内,已知$∠MON$,P是任意一点.若过点P画一条直线与OM平行,则这样的直线 (
A.有且只有一条
B.有两条
C.不存在
D.只有一条或不存在
D
)A.有且只有一条
B.有两条
C.不存在
D.只有一条或不存在
答案:【解析】:
本题考查平行线的概念及性质。
在同一平面内,若点P在直线$OM$上,则过点P无法画出与$OM$平行的直线(因为两直线重合不是平行的定义)。
若点P不在直线$OM$上,根据平行线的定义及性质,过点P可以画出且仅可以画出一条与$OM$平行的直线。
综合以上两种情况,这样的直线要么不存在(点P在$OM$上),要么有且仅有一条(点P不在$OM$上)。
【答案】:
D. 只有一条或不存在。
本题考查平行线的概念及性质。
在同一平面内,若点P在直线$OM$上,则过点P无法画出与$OM$平行的直线(因为两直线重合不是平行的定义)。
若点P不在直线$OM$上,根据平行线的定义及性质,过点P可以画出且仅可以画出一条与$OM$平行的直线。
综合以上两种情况,这样的直线要么不存在(点P在$OM$上),要么有且仅有一条(点P不在$OM$上)。
【答案】:
D. 只有一条或不存在。