10. 若a,b,c是同一平面内互不重合的三条直线,则它们的交点个数为 (
A.1或2或3
B.0或1或2或3
C.1或2
D.以上都不正确
B
)A.1或2或3
B.0或1或2或3
C.1或2
D.以上都不正确
答案:【解析】:
本题主要考查平面内三条直线交点个数的判断。
首先,我们考虑三条直线在同一平面内的各种可能情况:
1. 三条直线交于一点:这种情况下,三条直线只有一个共同的交点。
2. 三条直线两两相交,但交点不重合:这种情况下,有三条直线,每两条直线都有一个交点,且这三个交点都不相同,因此有3个交点。
3. 其中两条直线平行,另一条直线与这两条直线相交:在这种情况下,平行的两条直线没有交点,而第三条直线与这两条平行线分别相交于两点,因此有2个交点。
4. 三条直线互相平行:在这种情况下,三条直线之间不会有交点,即交点个数为0。
5. 三条直线重合:题目已明确说明三条直线“互不重合”,因此这种情况不在考虑范围内。
综合以上情况,我们可以得出结论:在同一平面内,三条互不重合的直线的交点个数可能是0个(三条直线都平行),1个(三条直线交于一点),2个(其中两条平行且被第三条直线截断),或3个(三条直线两两相交且交点不重合)。
【答案】:
B. 0或1或2或3。
本题主要考查平面内三条直线交点个数的判断。
首先,我们考虑三条直线在同一平面内的各种可能情况:
1. 三条直线交于一点:这种情况下,三条直线只有一个共同的交点。
2. 三条直线两两相交,但交点不重合:这种情况下,有三条直线,每两条直线都有一个交点,且这三个交点都不相同,因此有3个交点。
3. 其中两条直线平行,另一条直线与这两条直线相交:在这种情况下,平行的两条直线没有交点,而第三条直线与这两条平行线分别相交于两点,因此有2个交点。
4. 三条直线互相平行:在这种情况下,三条直线之间不会有交点,即交点个数为0。
5. 三条直线重合:题目已明确说明三条直线“互不重合”,因此这种情况不在考虑范围内。
综合以上情况,我们可以得出结论:在同一平面内,三条互不重合的直线的交点个数可能是0个(三条直线都平行),1个(三条直线交于一点),2个(其中两条平行且被第三条直线截断),或3个(三条直线两两相交且交点不重合)。
【答案】:
B. 0或1或2或3。
11. 已知a,b,c,d是同一平面内互不重合的四条直线.若$a// b,b// c,c// d$,则a与d之间的位置关系是
$a // d$
.答案:【解析】:
本题主要考查平行线的性质及传递性。在平面内,如果两条直线都与第三条直线平行,那么这两条直线也必定平行。由题意知,$a // b$,$b // c$,根据平行线的传递性,我们可以得出$a // c$。又因为$c // d$,所以再次根据平行线的传递性,我们可以得出$a // d$。
【答案】:
$a // d$
本题主要考查平行线的性质及传递性。在平面内,如果两条直线都与第三条直线平行,那么这两条直线也必定平行。由题意知,$a // b$,$b // c$,根据平行线的传递性,我们可以得出$a // c$。又因为$c // d$,所以再次根据平行线的传递性,我们可以得出$a // d$。
【答案】:
$a // d$
12. (2025·江苏常州期末)给出下列说法:
① 在同一平面内,两条不相交的线段平行;
② 在同一平面内,两条不相交的射线平行;
③ 在同一平面内,两条不相交的直线平行;
④ 在同一平面内,若直线$AB// CD$,直线AB与直线EF相交,则直线CD与直线EF相交.
其中错误的是____.(填序号)
① 在同一平面内,两条不相交的线段平行;
② 在同一平面内,两条不相交的射线平行;
③ 在同一平面内,两条不相交的直线平行;
④ 在同一平面内,若直线$AB// CD$,直线AB与直线EF相交,则直线CD与直线EF相交.
其中错误的是____.(填序号)
①②
答案:【解析】:
本题主要考查平行线的概念及性质。
首先分析每个说法的正确性:
① 在同一平面内,两条不相交的线段平行。这个说法是错误的,因为线段有固定的起点和终点,即使它们不相交,也不能直接判断它们平行,除非它们可以延长为不相交的直线。
② 在同一平面内,两条不相交的射线平行。这个说法也是错误的,射线有一个固定的起点但可以无限延伸,同样不能仅凭它们当前不相交就判断它们平行。
③ 在同一平面内,两条不相交的直线平行。这个说法是正确的,根据平行线的定义,同一平面内不相交的两条直线就是平行的。
④ 在同一平面内,若直线$AB//CD$,直线$AB$与直线$EF$相交,则直线$CD$与直线$EF$相交。这个说法是正确的,它体现了平行线的一个基本性质,即如果一条直线与平行线中的一条相交,那么它也必然与另一条相交。
综上所述,错误的说法有①和②。
【答案】:
①②
本题主要考查平行线的概念及性质。
首先分析每个说法的正确性:
① 在同一平面内,两条不相交的线段平行。这个说法是错误的,因为线段有固定的起点和终点,即使它们不相交,也不能直接判断它们平行,除非它们可以延长为不相交的直线。
② 在同一平面内,两条不相交的射线平行。这个说法也是错误的,射线有一个固定的起点但可以无限延伸,同样不能仅凭它们当前不相交就判断它们平行。
③ 在同一平面内,两条不相交的直线平行。这个说法是正确的,根据平行线的定义,同一平面内不相交的两条直线就是平行的。
④ 在同一平面内,若直线$AB//CD$,直线$AB$与直线$EF$相交,则直线$CD$与直线$EF$相交。这个说法是正确的,它体现了平行线的一个基本性质,即如果一条直线与平行线中的一条相交,那么它也必然与另一条相交。
综上所述,错误的说法有①和②。
【答案】:
①②
13. 在同一平面内,四条互不重合的直线的交点个数的所有可能值为
0,1,3,4,5,6
.答案:解:0,1,3,4,5,6
14. 新趋势 推导探究
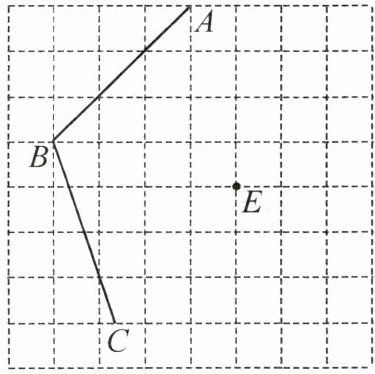
(1) 在如图所示的方格纸中,过点E画直线DE,EF,使$DE// AB,EF// BC$;
(2) 猜想:$∠ABC与∠DEF$之间有什么数量关系? (不用说明理由)
(3) 你能用量角器验证你的结论吗?
(1) 在如图所示的方格纸中,过点E画直线DE,EF,使$DE// AB,EF// BC$;
(2) 猜想:$∠ABC与∠DEF$之间有什么数量关系? (不用说明理由)
(3) 你能用量角器验证你的结论吗?

答案:【解析】:
(1) 此问主要考查平行线的画法。在方格纸中,利用方格的特点,通过数格子的方式,使直线$DE$经过的格子与$AB$经过的格子对应位置相同,从而画出$DE// AB$;同理画出$EF// BC$。
(2) 本题可根据平行线的性质来猜想$\angle ABC$与$\angle DEF$的数量关系。因为$DE// AB$,$EF// BC$,根据平行线的性质,两直线平行,同位角相等,所以可猜想$\angle ABC=\angle DEF$。
(3) 此问是实践操作题,用量角器分别测量$\angle ABC$和$\angle DEF$的度数,通过比较度数来验证(2)中的猜想。
【答案】:
(1) 图略(在方格纸中,通过数格子,使直线$DE$与$AB$方向相同,$EF$与$BC$方向相同画出即可)。
(2) $\angle ABC = \angle DEF$。
(3) 能。用量角器分别测量$\angle ABC$和$\angle DEF$的度数,会发现它们的度数相等,从而验证$\angle ABC=\angle DEF$的结论。
(1) 此问主要考查平行线的画法。在方格纸中,利用方格的特点,通过数格子的方式,使直线$DE$经过的格子与$AB$经过的格子对应位置相同,从而画出$DE// AB$;同理画出$EF// BC$。
(2) 本题可根据平行线的性质来猜想$\angle ABC$与$\angle DEF$的数量关系。因为$DE// AB$,$EF// BC$,根据平行线的性质,两直线平行,同位角相等,所以可猜想$\angle ABC=\angle DEF$。
(3) 此问是实践操作题,用量角器分别测量$\angle ABC$和$\angle DEF$的度数,通过比较度数来验证(2)中的猜想。
【答案】:
(1) 图略(在方格纸中,通过数格子,使直线$DE$与$AB$方向相同,$EF$与$BC$方向相同画出即可)。
(2) $\angle ABC = \angle DEF$。
(3) 能。用量角器分别测量$\angle ABC$和$\angle DEF$的度数,会发现它们的度数相等,从而验证$\angle ABC=\angle DEF$的结论。
15. (2025·江苏盐城期末)如图,在同一平面内,一组互相平行的直线共有n条(n为大于1的正整数),它们和两条平行线a,b相交,构成若干个“”字形,设构成的“”字形个数为x,请填写下表:




当n=2时,x=1;当n=3时,x=3;当n=4时,x=6;当n=5时,x=10;规律:x=n(n-1)/2
答案:解:当n=2时,x=1;
当n=3时,x=3;
当n=4时,x=6;
当n=5时,x=10;
...
规律:x=n(n-1)/2。
(注:由于题目未给出具体表格内容,根据常见“”字形个数规律补充,若表格有特定n值要求,需根据实际表格数据调整。此处按n=2,3,4,5时的结果填写。)
当n=3时,x=3;
当n=4时,x=6;
当n=5时,x=10;
...
规律:x=n(n-1)/2。
(注:由于题目未给出具体表格内容,根据常见“”字形个数规律补充,若表格有特定n值要求,需根据实际表格数据调整。此处按n=2,3,4,5时的结果填写。)
16. 新趋势 综合实践 如图,C为线段AB外一点,连接AC,BC,D,E,F是线段AB的四等分点.
(1) 过点D画$DH// BC$,交AC于点H,过点E画$EG// BC$,交AC于点G,过点F画$FM// BC$,交AC于点M;
(2) 量出线段AH,HG,GM,MC的长度,你有什么发现?
(3) 量出线段DH,EG,FM,BC的长度,你又有什么发现?

(1) 过点D画$DH// BC$,交AC于点H,过点E画$EG// BC$,交AC于点G,过点F画$FM// BC$,交AC于点M;
(2) 量出线段AH,HG,GM,MC的长度,你有什么发现?
(3) 量出线段DH,EG,FM,BC的长度,你又有什么发现?

答案:(1) 解:图略(按要求作出平行线DH、EG、FM)。
(2) 解:经测量,AH=HG=GM=MC。
(3) 解:经测量,DH:EG:FM:BC=1:2:3:4。
(2) 解:经测量,AH=HG=GM=MC。
(3) 解:经测量,DH:EG:FM:BC=1:2:3:4。