1. 如图,直线 $ a,b $ 被直线 $ c $ 所截,下列各组角是同位角的为 (
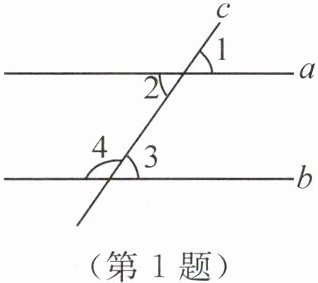
A.$ ∠1 $ 与 $ ∠2 $
B.$ ∠1 $ 与 $ ∠3 $
C.$ ∠2 $ 与 $ ∠3 $
D.$ ∠3 $ 与 $ ∠4 $
B
)
A.$ ∠1 $ 与 $ ∠2 $
B.$ ∠1 $ 与 $ ∠3 $
C.$ ∠2 $ 与 $ ∠3 $
D.$ ∠3 $ 与 $ ∠4 $
答案:解:同位角是指两条直线被第三条直线所截,在截线同旁,且在被截两直线同一侧的角。
观察图形:
选项A:∠1与∠2在截线c的两旁,不是同位角。
选项B:∠1与∠3在截线c的同旁,且分别在直线a、b的同一侧,是同位角。
选项C:∠2与∠3的位置不符合同位角定义。
选项D:∠3与∠4是邻补角,不是同位角。
答案:B
观察图形:
选项A:∠1与∠2在截线c的两旁,不是同位角。
选项B:∠1与∠3在截线c的同旁,且分别在直线a、b的同一侧,是同位角。
选项C:∠2与∠3的位置不符合同位角定义。
选项D:∠3与∠4是邻补角,不是同位角。
答案:B
2. (教材 $ P185 $ 练习 2 变式)如图,若 $ ∠1 = ∠2 $,则下列结论正确的是 (

A.$ AD // BC $
B.$ AB // CD $
C.$ AD // EF $
D.$ BC // EF $
C
)
A.$ AD // BC $
B.$ AB // CD $
C.$ AD // EF $
D.$ BC // EF $
答案:解:∵∠1与∠2是直线AD、EF被直线DF所截形成的同位角,且∠1=∠2,
∴AD//EF(同位角相等,两直线平行)。
答案:C
∴AD//EF(同位角相等,两直线平行)。
答案:C
3. 新素养 几何直观 在如图所示的四个图形中,$ ∠1 $ 和 $ ∠2 $ 是同位角的为 (
 A. ②③ B. ①②③
A. ②③ B. ①②③
C. ①②④ D. ①④
C
) A. ②③ B. ①②③
A. ②③ B. ①②③C. ①②④ D. ①④
答案:解:同位角的定义:两条直线被第三条直线所截,在截线的同旁,被截两直线的同一侧的角,我们把这样的两个角称为同位角。
①中,∠1和∠2是两条直线被第三条直线所截形成的同位角;
②中,∠1和∠2是两条直线被第三条直线所截形成的同位角;
③中,∠1和∠2的边所在直线不是两条直线被第三条直线所截的情况,不是同位角;
④中,∠1和∠2是两条直线被第三条直线所截形成的同位角。
所以∠1和∠2是同位角的为①②④。
答案:C
①中,∠1和∠2是两条直线被第三条直线所截形成的同位角;
②中,∠1和∠2是两条直线被第三条直线所截形成的同位角;
③中,∠1和∠2的边所在直线不是两条直线被第三条直线所截的情况,不是同位角;
④中,∠1和∠2是两条直线被第三条直线所截形成的同位角。
所以∠1和∠2是同位角的为①②④。
答案:C
4. 如图,$ ∠1 $ 和 $ ∠2 $ 是
同位角
,它们是直线AB
和AC
被直线DE
所截而成的;$ ∠3 $ 和 $ ∠4 $ 是同位角
,它们是直线AB
和BC
被直线DE
所截而成的.答案:同位角;AB;AC;DE;同位角;AB;BC;DE
5. 如图,直线 $ a,b $ 被直线 $ c $ 所截,当 $ ∠1 $

=
$ ∠2 $ 时,$ a // b $.(填“$ > $”“$ < $”或“$ = $”)
答案:【解析】:
本题考查同位角判定两直线平行的知识点,同位角相等,两直线平行是基本的几何定理,题目给出了两条直线$a$,$b$被直线$c$所截形成的同位角$∠1$和$∠2$,要求判断当两直线平行时,这两个角的关系。
根据同位角相等,两直线平行的定理,我们可以直接得出答案,即当$∠1=∠2$时,$a//b$。
【答案】:
$=$
本题考查同位角判定两直线平行的知识点,同位角相等,两直线平行是基本的几何定理,题目给出了两条直线$a$,$b$被直线$c$所截形成的同位角$∠1$和$∠2$,要求判断当两直线平行时,这两个角的关系。
根据同位角相等,两直线平行的定理,我们可以直接得出答案,即当$∠1=∠2$时,$a//b$。
【答案】:
$=$
6. 如图,若 $ ∠1 = 100° $,则图中 $ ∠2 $ 的同位角的度数为
$80^{\circ}$
.答案:180°-100°=80°
7. 如图,已知 $ ∠1 = ∠2 = 115^\circ $,$ ∠3 = 65^\circ $,图中有哪些直线互相平行? 为什么?


答案:解:图中平行的直线有AB//MD,GN//HC。
理由:
∵∠1=115°,∠3=65°,∠4与∠3是对顶角,
∴∠4=∠3=65°,
∴∠1+∠4=115°+65°=180°,
∴AB//MD(同旁内角互补,两直线平行)。
∵∠2=115°,∠4=65°,
∴∠2+∠4=115°+65°=180°,
∴GN//HC(同旁内角互补,两直线平行)。
理由:
∵∠1=115°,∠3=65°,∠4与∠3是对顶角,
∴∠4=∠3=65°,
∴∠1+∠4=115°+65°=180°,
∴AB//MD(同旁内角互补,两直线平行)。
∵∠2=115°,∠4=65°,
∴∠2+∠4=115°+65°=180°,
∴GN//HC(同旁内角互补,两直线平行)。
8. 如图,与 $ ∠1 $ 是同位角的为 (

A.$ ∠2 $
B.$ ∠3 $
C.$ ∠4 $
D.$ ∠5 $
D
)
A.$ ∠2 $
B.$ ∠3 $
C.$ ∠4 $
D.$ ∠5 $
答案:解:根据同位角的定义,两条直线被第三条直线所截,在截线同旁,且在被截两直线同一侧的角为同位角。观察图形可知,∠1与∠5是同位角。
答案:D
答案:D
9. 如图,已知 $ ∠1 = 90° $,为保证两条铁轨平行,添加的下列条件中,正确的是 (

A.$ ∠2 = 90° $
B.$ ∠3 = 90° $
C.$ ∠4 = 90° $
D.$ ∠5 = 90° $
C
) 
A.$ ∠2 = 90° $
B.$ ∠3 = 90° $
C.$ ∠4 = 90° $
D.$ ∠5 = 90° $
答案:【解析】:
本题考查同位角判定两直线平行的知识点,要使两条铁轨平行,需要找到同位角相等的条件,已知$\angle1=90°$,分析各个选项,判断哪个角与$\angle1$构成同位角且相等,从而保证两条铁轨平行。
选项A,若$\angle2=90°$,$\angle1$与$\angle2$是同旁内角,同旁内角相等两直线不一定平行,所以该选项错误。
选项B,若$\angle3=90°$,$\angle1$与$\angle3$既不是同位角,也不是内错角和同旁内角,无法根据此判断两条铁轨平行,所以该选项错误。
选项C,若$\angle4=90°$,$\angle1$与$\angle4$是同位角,且$\angle1=\angle4=90°$,根据同位角相等,两直线平行,可以保证两条铁轨平行,所以该选项正确。
选项D,若$\angle5=90°$,$\angle1$与$\angle5$既不是同位角,也不是内错角和同旁内角,无法根据此判断两条铁轨平行,所以该选项错误。
答:本题答案选C。
【答案】:C
本题考查同位角判定两直线平行的知识点,要使两条铁轨平行,需要找到同位角相等的条件,已知$\angle1=90°$,分析各个选项,判断哪个角与$\angle1$构成同位角且相等,从而保证两条铁轨平行。
选项A,若$\angle2=90°$,$\angle1$与$\angle2$是同旁内角,同旁内角相等两直线不一定平行,所以该选项错误。
选项B,若$\angle3=90°$,$\angle1$与$\angle3$既不是同位角,也不是内错角和同旁内角,无法根据此判断两条铁轨平行,所以该选项错误。
选项C,若$\angle4=90°$,$\angle1$与$\angle4$是同位角,且$\angle1=\angle4=90°$,根据同位角相等,两直线平行,可以保证两条铁轨平行,所以该选项正确。
选项D,若$\angle5=90°$,$\angle1$与$\angle5$既不是同位角,也不是内错角和同旁内角,无法根据此判断两条铁轨平行,所以该选项错误。
答:本题答案选C。
【答案】:C