10. 如图,直线 $ a $ 与直线 $ b $ 被直线 $ c $ 所截,$ b ⊥ c $,垂足为 $ A $,$ ∠1 = 70^\circ $.若使直线 $ b $ 与直线 $ a $ 平行,则直线 $ b $ 绕着点 $ A $ 顺时针旋转的角度可以为 (
A.$ 70^\circ $
B.$ 50^\circ $
C.$ 30^\circ $
D.$ 20^\circ $
D
)A.$ 70^\circ $
B.$ 50^\circ $
C.$ 30^\circ $
D.$ 20^\circ $
答案：【解析】：本题考查同位角判定两直线平行的知识点。
首先，我们知道直线b与直线c垂直，所以$\angle bAc= 90^\circ$。
然后，根据同位角相等，两直线平行，要使直线b与直线a平行，
我们需要找到一个角度，使得直线b绕着点A顺时针旋转后，与直线a形成的同位角相等。
观察图形可知，这个同位角其实就是$\angle 1$的补角，即$180^\circ - \angle 1 = 180^\circ - 70^\circ = 110^\circ$。
但是，这个$110^\circ$是直线b与直线c的夹角，而我们需要的是直线b绕着点A顺时针旋转的角度。
由于直线b与直线c原本垂直，即夹角为$90^\circ$，
所以我们需要旋转的角度就是$110^\circ - 90^\circ = 20^\circ$。
【答案】：D
首先，我们知道直线b与直线c垂直，所以$\angle bAc= 90^\circ$。
然后，根据同位角相等，两直线平行，要使直线b与直线a平行，
我们需要找到一个角度，使得直线b绕着点A顺时针旋转后，与直线a形成的同位角相等。
观察图形可知，这个同位角其实就是$\angle 1$的补角，即$180^\circ - \angle 1 = 180^\circ - 70^\circ = 110^\circ$。
但是，这个$110^\circ$是直线b与直线c的夹角，而我们需要的是直线b绕着点A顺时针旋转的角度。
由于直线b与直线c原本垂直，即夹角为$90^\circ$，
所以我们需要旋转的角度就是$110^\circ - 90^\circ = 20^\circ$。
【答案】：D
11. 如图,把三角板的直角顶点放在直线 $ b $ 上.若 $ ∠1 = 40^\circ $,则当 $ ∠2 = $
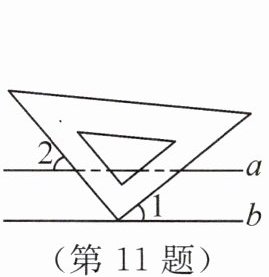
$50^{\circ}$
时,$ a // b $.答案：【解析】：本题可根据同位角相等两直线平行的判定定理来求解$∠2$的度数。
已知三角板的直角顶点放在直线$b$上，$∠1 = 40^{\circ}$，三角板的直角为$90^{\circ}$。
因为直线$a$、$b$与三角板的边构成了一个平角，平角为$180^{\circ}$，当$a// b$时，$∠1$与$∠2$和直角组成的另一个角是同位角，根据同位角相等，两直线平行，可知$∠1$与$∠2$和直角组成的另一个角相等。
先求出$∠2$和直角组成的另一个角的度数为$180^{\circ}-90^{\circ}-∠1$，将$∠1 = 40^{\circ}$代入可得：$180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$，所以当$∠2 = 50^{\circ}$时，同位角相等，$a// b$。
【答案】：$50^{\circ}$
已知三角板的直角顶点放在直线$b$上，$∠1 = 40^{\circ}$，三角板的直角为$90^{\circ}$。
因为直线$a$、$b$与三角板的边构成了一个平角，平角为$180^{\circ}$，当$a// b$时，$∠1$与$∠2$和直角组成的另一个角是同位角，根据同位角相等，两直线平行，可知$∠1$与$∠2$和直角组成的另一个角相等。
先求出$∠2$和直角组成的另一个角的度数为$180^{\circ}-90^{\circ}-∠1$，将$∠1 = 40^{\circ}$代入可得：$180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$，所以当$∠2 = 50^{\circ}$时，同位角相等，$a// b$。
【答案】：$50^{\circ}$
12. 如图,已知 $ EF ⊥ MN $ 于点 $ F $,且 $ ∠1 = 140^\circ $,则当 $ ∠2 = $
$50^\circ$
时,$ AB // CD $.答案：【解析】：本题主要考查了平行线的判定以及垂直的性质。
题目给出了$EF\perp MN$于点$F$，即$\angle EFN = 90^\circ$，同时给出了$\angle 1 = 140^\circ$。
由于$\angle 1$和$\angle 3$是对顶角，根据对顶角相等的性质，有$\angle 3 = \angle 1 = 140^\circ$。
为了找出$\angle 2$和$\angle 3$之间的关系，我们可以延长$EF$交$AB$于点$G$。
由于$EF$是垂直于$MN$的，所以$\angle GFM = 90^\circ$。
根据平行线的判定定理，如果同旁内角互补，即$\angle 2 + \angle 3 = 180^\circ$，则$AB// CD$。
现在我们已经知道$\angle 3 = 140^\circ$，所以可以通过计算找出$\angle 2$的值：$\angle 2 = 180^\circ - \angle 3 = 180^\circ - 140^\circ = 50^\circ$，但由于$EF\perp MN$，
所以实际上我们应该考虑的是$\angle 2$和$\angle EFD$（即直角$\angle EFN$的补角）的关系。
由于$\angle EFD = 90^\circ$，且$\angle 2$和$\angle EFD$是同旁内角，所以$\angle 2$应该是$180^\circ - 140^\circ+ 90^\circ-90^\circ= 50^\circ-0^\circ+0^\circ=50^\circ- \angle EFD$的补角，即$90^\circ - (140^\circ- 90^\circ) = 50^\circ$（这里直接通过几何关系得出$\angle 2 = 50^\circ$更直观）。
【答案】：$50^\circ$。
题目给出了$EF\perp MN$于点$F$，即$\angle EFN = 90^\circ$，同时给出了$\angle 1 = 140^\circ$。
由于$\angle 1$和$\angle 3$是对顶角，根据对顶角相等的性质，有$\angle 3 = \angle 1 = 140^\circ$。
为了找出$\angle 2$和$\angle 3$之间的关系，我们可以延长$EF$交$AB$于点$G$。
由于$EF$是垂直于$MN$的，所以$\angle GFM = 90^\circ$。
根据平行线的判定定理，如果同旁内角互补，即$\angle 2 + \angle 3 = 180^\circ$，则$AB// CD$。
现在我们已经知道$\angle 3 = 140^\circ$，所以可以通过计算找出$\angle 2$的值：$\angle 2 = 180^\circ - \angle 3 = 180^\circ - 140^\circ = 50^\circ$，但由于$EF\perp MN$，
所以实际上我们应该考虑的是$\angle 2$和$\angle EFD$（即直角$\angle EFN$的补角）的关系。
由于$\angle EFD = 90^\circ$，且$\angle 2$和$\angle EFD$是同旁内角，所以$\angle 2$应该是$180^\circ - 140^\circ+ 90^\circ-90^\circ= 50^\circ-0^\circ+0^\circ=50^\circ- \angle EFD$的补角，即$90^\circ - (140^\circ- 90^\circ) = 50^\circ$（这里直接通过几何关系得出$\angle 2 = 50^\circ$更直观）。
【答案】：$50^\circ$。
13. (2025·江苏连云港期末)如图,能判定 $ DE // BC $ 的相等的同位角有____对.
答案：答案略
解析：
由于题目中未提供具体的图形（插图1和插图2），无法准确判断能判定$DE // BC$的相等同位角的对数，因此无法完成作答。
1
1
14. 新素养 推理能力 如图,直线 $ AB,CD $ 被直线 $ EF $ 所截,$ H $ 为直线 $ CD $ 与 $ EF $ 的交点,$ GH ⊥ CD $,$ ∠2 = 30^\circ $,$ ∠1 = 60^\circ $.试说明:$ AB // CD $.
答案：证明：
∵GH⊥CD（已知），
∴∠CHG=90°（垂直的定义）．
∵∠2=30°（已知），∠CHG=∠2+∠3（角的和差），
∴∠3=∠CHG-∠2=90°-30°=60°．
∵∠4与∠3是对顶角（对顶角定义），
∴∠4=∠3=60°（对顶角相等）．
∵∠1=60°（已知），
∴∠1=∠4（等量代换）．
∵∠1与∠4是直线AB，CD被直线EF所截形成的同位角，
∴AB//CD（同位角相等，两直线平行）．
∵GH⊥CD（已知），
∴∠CHG=90°（垂直的定义）．
∵∠2=30°（已知），∠CHG=∠2+∠3（角的和差），
∴∠3=∠CHG-∠2=90°-30°=60°．
∵∠4与∠3是对顶角（对顶角定义），
∴∠4=∠3=60°（对顶角相等）．
∵∠1=60°（已知），
∴∠1=∠4（等量代换）．
∵∠1与∠4是直线AB，CD被直线EF所截形成的同位角，
∴AB//CD（同位角相等，两直线平行）．
15. (2025·江苏无锡期末)一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这辆汽车两次拐弯的角度可能是 (
A.第一次向右拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
B.第一次向右拐 $ 40^\circ $,第二次向左拐 $ 40^\circ $
C.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
D.第一次向右拐 $ 140^\circ $,第二次向右拐 $ 40^\circ $
B
)A.第一次向右拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
B.第一次向右拐 $ 40^\circ $,第二次向左拐 $ 40^\circ $
C.第一次向左拐 $ 40^\circ $,第二次向右拐 $ 140^\circ $
D.第一次向右拐 $ 140^\circ $,第二次向右拐 $ 40^\circ $
答案：【解析】：
本题主要考察平行线的性质，即如果两条直线被第三条直线所截，且同位角相等，则这两条直线平行。
汽车在草原上行驶，可以看作是在一条直线（原行驶方向）上行驶，两次拐弯可以看作是两条相交的直线与原行驶方向形成的夹角。
要使行驶方向与原来相同，需要两次拐弯形成的同位角相等或者两次拐弯的角度和为$180^\circ$且方向相反（即一次左拐，一次右拐，且角度相等）。
A选项：两次都向右拐，且角度和为$180^\circ$，但方向相同，不符合条件。
B选项：第一次向右拐$40^\circ$，第二次向左拐$40^\circ$，形成同位角，角度相等，符合条件。
C选项：第一次向左拐$40^\circ$，第二次向右拐$140^\circ$，角度和虽为$180^\circ$，但方向不同，不符合条件。
D选项：两次都向右拐，且角度和不为$180^\circ$，方向相同，不符合条件。
【答案】：
B
本题主要考察平行线的性质，即如果两条直线被第三条直线所截，且同位角相等，则这两条直线平行。
汽车在草原上行驶，可以看作是在一条直线（原行驶方向）上行驶，两次拐弯可以看作是两条相交的直线与原行驶方向形成的夹角。
要使行驶方向与原来相同，需要两次拐弯形成的同位角相等或者两次拐弯的角度和为$180^\circ$且方向相反（即一次左拐，一次右拐，且角度相等）。
A选项：两次都向右拐，且角度和为$180^\circ$，但方向相同，不符合条件。
B选项：第一次向右拐$40^\circ$，第二次向左拐$40^\circ$，形成同位角，角度相等，符合条件。
C选项：第一次向左拐$40^\circ$，第二次向右拐$140^\circ$，角度和虽为$180^\circ$，但方向不同，不符合条件。
D选项：两次都向右拐，且角度和不为$180^\circ$，方向相同，不符合条件。
【答案】：
B
16. 如图,直线 $ AB,CD $ 相交于点 $ O $,$ OD $ 平分 $ ∠BOE $,$ OF $ 平分 $ ∠AOE $,$ GH ⊥ CD $,垂足为 $ H $.试说明:$ GH // OF $.
答案：证明：
∵OD平分∠BOE，
∴∠DOE=∠BOD=1/2∠BOE，
∵OF平分∠AOE，
∴∠EOF=∠AOF=1/2∠AOE，
∵∠AOE+∠BOE=180°（邻补角互补），
∴∠EOF+∠DOE=1/2(∠AOE+∠BOE)=90°，即∠FOD=90°，
∵GH⊥CD，
∴∠GHO=90°，
∴∠GHO=∠FOD，
∴GH//OF（同位角相等，两直线平行）．
∵OD平分∠BOE，
∴∠DOE=∠BOD=1/2∠BOE，
∵OF平分∠AOE，
∴∠EOF=∠AOF=1/2∠AOE，
∵∠AOE+∠BOE=180°（邻补角互补），
∴∠EOF+∠DOE=1/2(∠AOE+∠BOE)=90°，即∠FOD=90°，
∵GH⊥CD，
∴∠GHO=90°，
∴∠GHO=∠FOD，
∴GH//OF（同位角相等，两直线平行）．
17. 新趋势 推导探究 如图,直线 $ AB,CD $ 分别与直线 $ EF $ 相交于点 $ G,H $.小明认为若 $ ∠1 = ∠2 $,则根据“同位角相等,两直线平行”可以知道直线 $ AB // CD $.你同意他的说法吗? 如果同意,请把你的理由写下来;如果不同意,再补充合适的条件使得 $ AB // CD $,并说明理由.
答案：不同意。
补充条件：GM和HN是射线（或GM、HN分别在AB、CD上）。
理由：若GM和HN是射线，则∠1和∠2是直线AB、CD被EF所截形成的同位角。因为∠1=∠2，所以根据“同位角相等，两直线平行”，可得AB//CD。
补充条件：GM和HN是射线（或GM、HN分别在AB、CD上）。
理由：若GM和HN是射线，则∠1和∠2是直线AB、CD被EF所截形成的同位角。因为∠1=∠2，所以根据“同位角相等，两直线平行”，可得AB//CD。