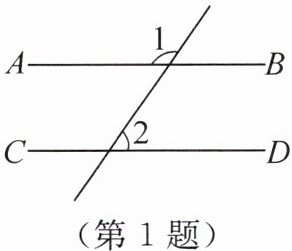
1. (教材P191习题4变式)(2024·重庆)如图,AB//CD.若∠1= 125°,则∠2的度数为 (
A.35°
B.45°
C.55°
D.125°
C
)
A.35°
B.45°
C.55°
D.125°
答案:【解析】:本题可根据平行线的性质求出与$\angle1$互补的角的度数,再结合该角与$\angle2$是对顶角,进而求出$\angle2$的度数。
步骤一:根据平行线的性质求出与$\angle1$互补的角的度数
已知$AB// CD$,$\angle1 = 125^{\circ}$。
根据“两直线平行,同旁内角互补”,可知$\angle1$与$\angle1$的同旁内角(即$\angle2$的对顶角)互补,即这两个角的和为$180^{\circ}$。
设$\angle2$的对顶角为$\angle3$,则$\angle1 + \angle3 = 180^{\circ}$,所以$\angle3 = 180^{\circ} - \angle1 = 180^{\circ} - 125^{\circ} = 55^{\circ}$。
步骤二:根据对顶角的性质求出$\angle2$的度数
因为$\angle2$与$\angle3$是对顶角,根据“对顶角相等”,可得$\angle2 = \angle3 = 55^{\circ}$。
【答案】:C
步骤一:根据平行线的性质求出与$\angle1$互补的角的度数
已知$AB// CD$,$\angle1 = 125^{\circ}$。
根据“两直线平行,同旁内角互补”,可知$\angle1$与$\angle1$的同旁内角(即$\angle2$的对顶角)互补,即这两个角的和为$180^{\circ}$。
设$\angle2$的对顶角为$\angle3$,则$\angle1 + \angle3 = 180^{\circ}$,所以$\angle3 = 180^{\circ} - \angle1 = 180^{\circ} - 125^{\circ} = 55^{\circ}$。
步骤二:根据对顶角的性质求出$\angle2$的度数
因为$\angle2$与$\angle3$是对顶角,根据“对顶角相等”,可得$\angle2 = \angle3 = 55^{\circ}$。
【答案】:C
2. (2025·江苏盐城期末)如图,已知AB与CD相交于点O.若∠A= ∠B= 30°,∠C= 50°,则∠D的度数为 (
A.20°
B.30°
C.40°
D.50°
D
)A.20°
B.30°
C.40°
D.50°
答案:解:在△AOC中,∠A=30°,∠C=50°,
∠AOC=180°-∠A-∠C=180°-30°-50°=100°。
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=100°。
在△BOD中,∠B=30°,∠BOD=100°,
∠D=180°-∠B-∠BOD=180°-30°-100°=50°。
答案:D
∠AOC=180°-∠A-∠C=180°-30°-50°=100°。
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=100°。
在△BOD中,∠B=30°,∠BOD=100°,
∠D=180°-∠B-∠BOD=180°-30°-100°=50°。
答案:D
3. 如图,已知AB//CD//EF.若∠ABC= 130°,∠BCE= 55°,则∠CEF的度数为 (

A.95°
B.105°
C.110°
D.115°
B
)
A.95°
B.105°
C.110°
D.115°
答案:解:
∵AB//CD,∠ABC=130°,
∴∠BCD=∠ABC=130°(两直线平行,内错角相等)。
∵∠BCE=55°,
∴∠ECD=∠BCD - ∠BCE=130° - 55°=75°。
∵CD//EF,
∴∠CEF + ∠ECD=180°(两直线平行,同旁内角互补),
∴∠CEF=180° - ∠ECD=180° - 75°=105°。
答案:B
∵AB//CD,∠ABC=130°,
∴∠BCD=∠ABC=130°(两直线平行,内错角相等)。
∵∠BCE=55°,
∴∠ECD=∠BCD - ∠BCE=130° - 55°=75°。
∵CD//EF,
∴∠CEF + ∠ECD=180°(两直线平行,同旁内角互补),
∴∠CEF=180° - ∠ECD=180° - 75°=105°。
答案:B
4. 如图,已知直线a//b,∠BAC= 90°,∠1= 50°,则∠2=
40°
.答案:【解析】:本题主要考查平行线的性质以及直角三角形的性质。
因为直线a平行于直线b,根据平行线的性质“两直线平行,同位角相等”,可知∠2与∠ABC的同位角相等,所以我们可以先求出∠ABC的度数,进而得到∠2的度数。
在$\bigtriangleup ABC$中,已知$\angle BAC = 90^{\circ}$,$\angle 1 = 50^{\circ}$,根据三角形内角和为$180^{\circ}$,可求出$\angle ABC$的度数,即$\angle ABC=180^{\circ}-\angle BAC - \angle 1$。
【答案】:在$\bigtriangleup ABC$中,
$\angle ABC = 180^{\circ} - \angle BAC - \angle 1$
$= 180^{\circ} - 90^{\circ} - 50^{\circ}$
$= 40^{\circ}$
因为$a// b$,根据两直线平行,同位角相等,$\angle 2$与$\angle ABC$的同位角相等,所以$\angle 2 = \angle ABC = 40^{\circ}$。
故答案为:$40^{\circ}$。
因为直线a平行于直线b,根据平行线的性质“两直线平行,同位角相等”,可知∠2与∠ABC的同位角相等,所以我们可以先求出∠ABC的度数,进而得到∠2的度数。
在$\bigtriangleup ABC$中,已知$\angle BAC = 90^{\circ}$,$\angle 1 = 50^{\circ}$,根据三角形内角和为$180^{\circ}$,可求出$\angle ABC$的度数,即$\angle ABC=180^{\circ}-\angle BAC - \angle 1$。
【答案】:在$\bigtriangleup ABC$中,
$\angle ABC = 180^{\circ} - \angle BAC - \angle 1$
$= 180^{\circ} - 90^{\circ} - 50^{\circ}$
$= 40^{\circ}$
因为$a// b$,根据两直线平行,同位角相等,$\angle 2$与$\angle ABC$的同位角相等,所以$\angle 2 = \angle ABC = 40^{\circ}$。
故答案为:$40^{\circ}$。
5. (2023·湖南永州)如图,AB//CD,BC//ED.若∠B= 80°,则∠D= ______.


100°
答案:【解析】:本题可根据平行线的性质来求解$\angle D$的度数。
已知$AB// CD$,根据两直线平行,同位角相等,可得$\angle B$与$\angle C$是同位角,所以$\angle C = \angle B = 80^{\circ}$。
又因为$BC// ED$,根据两直线平行,同旁内角互补,可知$\angle C$与$\angle D$是同旁内角,所以$\angle C + \angle D = 180^{\circ}$。
将$\angle C = 80^{\circ}$代入$\angle C + \angle D = 180^{\circ}$,即可求出$\angle D$的度数。
【答案】:解:
∵$AB// CD$,$\angle B = 80^{\circ}$,
∴$\angle C = \angle B = 80^{\circ}$(两直线平行,同位角相等)。
∵$BC// ED$,
∴$\angle C + \angle D = 180^{\circ}$(两直线平行,同旁内角互补)。
∴$\angle D = 180^{\circ} - \angle C = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
故答案为$100^{\circ}$。
已知$AB// CD$,根据两直线平行,同位角相等,可得$\angle B$与$\angle C$是同位角,所以$\angle C = \angle B = 80^{\circ}$。
又因为$BC// ED$,根据两直线平行,同旁内角互补,可知$\angle C$与$\angle D$是同旁内角,所以$\angle C + \angle D = 180^{\circ}$。
将$\angle C = 80^{\circ}$代入$\angle C + \angle D = 180^{\circ}$,即可求出$\angle D$的度数。
【答案】:解:
∵$AB// CD$,$\angle B = 80^{\circ}$,
∴$\angle C = \angle B = 80^{\circ}$(两直线平行,同位角相等)。
∵$BC// ED$,
∴$\angle C + \angle D = 180^{\circ}$(两直线平行,同旁内角互补)。
∴$\angle D = 180^{\circ} - \angle C = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
故答案为$100^{\circ}$。
6. 如图,已知AB//CD,AB⊥AE,∠CAE= 42°,则∠ACD的度数为________.


132°
答案:132°
7. 如图,已知直线AB//CD,BC平分∠ABD.若∠1= 54°,求∠2的度数.


答案:【解析】:本题主要考查平行线的性质以及角平分线的定义。根据平行线的性质,两直线平行,内错角相等,可得$\angle ABC = \angle 1$。再根据角平分线的定义,$BC$平分$\angle ABD$,所以$\angle ABD = 2\angle ABC$。最后利用邻补角的性质求出$\angle 2$的度数。
【答案】:解:
∵$AB// CD$,$\angle 1 = 54^{\circ}$,
∴$\angle ABC = \angle 1 = 54^{\circ}$(两直线平行,内错角相等)。
∵$BC$平分$\angle ABD$,
∴$\angle ABD = 2\angle ABC = 2×54^{\circ} = 108^{\circ}$(角平分线的定义)。
∵$\angle 2$与$\angle ABD$互为邻补角,
∴$\angle 2 = 180^{\circ} - \angle ABD = 180^{\circ} - 108^{\circ} = 72^{\circ}$(邻补角的性质)。
综上,$\angle 2$的度数为$72^{\circ}$。
【答案】:解:
∵$AB// CD$,$\angle 1 = 54^{\circ}$,
∴$\angle ABC = \angle 1 = 54^{\circ}$(两直线平行,内错角相等)。
∵$BC$平分$\angle ABD$,
∴$\angle ABD = 2\angle ABC = 2×54^{\circ} = 108^{\circ}$(角平分线的定义)。
∵$\angle 2$与$\angle ABD$互为邻补角,
∴$\angle 2 = 180^{\circ} - \angle ABD = 180^{\circ} - 108^{\circ} = 72^{\circ}$(邻补角的性质)。
综上,$\angle 2$的度数为$72^{\circ}$。
8. (2024·内蒙古包头)如图,直线AB//CD,点E在直线AB上,射线EF交直线CD于点G,则图中与∠AEF互补的角有 (

A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:【解析】:本题可根据平行线的性质以及互补角的定义来找出与$\angle AEF$互补的角。
互补角的定义为:如果两个角的和是$180^{\circ}$,那么这两个角互为补角。
已知$AB// CD$,$\angle AEF$与它的邻补角互补,$\angle AEF$的邻补角是$\angle BEF$,所以$\angle AEF$与$\angle BEF$互补。
根据两直线平行,同旁内角互补,因为$AB// CD$,$\angle AEF$与$\angle EGD$是同旁内角,所以$\angle AEF+\angle EGD = 180^{\circ}$,即$\angle AEF$与$\angle EGD$互补。
又因为$\angle EGD$与$\angle CGF$是对顶角,对顶角相等,所以$\angle EGD=\angle CGF$,那么$\angle AEF$与$\angle CGF$也互补。
综上,与$\angle AEF$互补的角有$\angle BEF$,$\angle EGD$,$\angle CGF$,共$3$个。
【答案】:C
互补角的定义为:如果两个角的和是$180^{\circ}$,那么这两个角互为补角。
已知$AB// CD$,$\angle AEF$与它的邻补角互补,$\angle AEF$的邻补角是$\angle BEF$,所以$\angle AEF$与$\angle BEF$互补。
根据两直线平行,同旁内角互补,因为$AB// CD$,$\angle AEF$与$\angle EGD$是同旁内角,所以$\angle AEF+\angle EGD = 180^{\circ}$,即$\angle AEF$与$\angle EGD$互补。
又因为$\angle EGD$与$\angle CGF$是对顶角,对顶角相等,所以$\angle EGD=\angle CGF$,那么$\angle AEF$与$\angle CGF$也互补。
综上,与$\angle AEF$互补的角有$\angle BEF$,$\angle EGD$,$\angle CGF$,共$3$个。
【答案】:C
9. 如图,将四边形纸片ABCD沿BD折叠,得到三角形BC'D,C'D与AB交于点E.若CD//AB,∠1= 35°,∠C= 90°,则∠2的度数为 (
A.20°
B.30°
C.35°
D.55°
A
)A.20°
B.30°
C.35°
D.55°
答案:解:∵CD//AB,∠1=35°,
∴∠CDB=∠ABD=35°(两直线平行,内错角相等)。
∵∠C=90°,
∴∠CBD=90°-∠CDB=90°-35°=55°。
由折叠性质得∠C'BD=∠CBD=55°。
∴∠2=∠C'BD-∠ABD=55°-35°=20°。
答案:A
∴∠CDB=∠ABD=35°(两直线平行,内错角相等)。
∵∠C=90°,
∴∠CBD=90°-∠CDB=90°-35°=55°。
由折叠性质得∠C'BD=∠CBD=55°。
∴∠2=∠C'BD-∠ABD=55°-35°=20°。
答案:A