10. 如图,已知AB//CD,EC⊥CD,CF交AB于点B.若∠2= 29°,则∠1的度数是 (
A.58°
B.59°
C.61°
D.62°
C
)A.58°
B.59°
C.61°
D.62°
答案:【解析】:本题可根据平行线的性质以及垂直的性质来求解$\angle1$的度数。
步骤一:根据垂直的性质求出$\angle ECD$的度数
已知$EC\perp CD$,根据垂直的定义:如果两条直线相交成直角,那么这两条直线互相垂直,可知$\angle ECD = 90^{\circ}$。
步骤二:根据直角三角形的性质求出$\angle DBC$的度数
在$\triangle BCD$中,$\angle ECD = 90^{\circ}$,$\angle 2 = 29^{\circ}$,因为$\angle ECD=\angle 2+\angle DBC$,所以$\angle DBC=\angle ECD - \angle 2=90^{\circ}-29^{\circ}=61^{\circ}$。
步骤三:根据平行线的性质求出$\angle1$的度数
因为$AB// CD$,根据两直线平行,同位角相等,可知$\angle1$和$\angle DBC$是同位角,所以$\angle1 = \angle DBC = 61^{\circ}$。
【答案】:C
步骤一:根据垂直的性质求出$\angle ECD$的度数
已知$EC\perp CD$,根据垂直的定义:如果两条直线相交成直角,那么这两条直线互相垂直,可知$\angle ECD = 90^{\circ}$。
步骤二:根据直角三角形的性质求出$\angle DBC$的度数
在$\triangle BCD$中,$\angle ECD = 90^{\circ}$,$\angle 2 = 29^{\circ}$,因为$\angle ECD=\angle 2+\angle DBC$,所以$\angle DBC=\angle ECD - \angle 2=90^{\circ}-29^{\circ}=61^{\circ}$。
步骤三:根据平行线的性质求出$\angle1$的度数
因为$AB// CD$,根据两直线平行,同位角相等,可知$\angle1$和$\angle DBC$是同位角,所以$\angle1 = \angle DBC = 61^{\circ}$。
【答案】:C
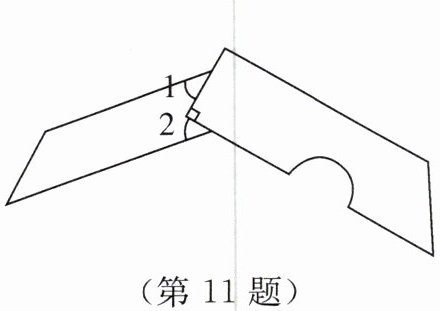
11. 新素养 几何直观 如图,梯形刀片的上、下边是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= ______.



180°
答案:解:过∠1和∠2的公共顶点作梯形上下边的平行线,根据两直线平行,内错角相等,可得∠1和∠2分别等于所作平行线与刀片两边形成的内错角,这两个内错角之和为180°,故∠1+∠2=180°。
180°
180°
12. (2025·江苏淮安期末)如图,直线EF分别交直线AB,CD于点G,H,AB//CD,MG⊥EF,HN平分∠CHG.若∠CHN= 32°,则∠AGM= ______
26°
.答案:【解析】:
本题主要考查平行线的性质、垂直的定义以及角平分线的定义。
首先,由于$HN$平分$\angle CHG$,且$\angle CHN = 32^\circ$,根据角平分线的定义,我们可以得出:
$\angle CHG = 2 × \angle CHN = 2 × 32^\circ = 64^\circ$,
接着,由于$AB // CD$,根据平行线的性质,我们有:
$\angle AGH = \angle CHG = 64^\circ$,(内错角相等),
最后,由于$MG \perp EF$,根据垂直的定义,我们知道$\angle MGH = 90^\circ$。
因此,我们可以求出$\angle AGM$:
$\angle AGM = 90^\circ - \angle AGH = 90^\circ - 64^\circ = 26^\circ$。
【答案】:
$26^\circ$。
本题主要考查平行线的性质、垂直的定义以及角平分线的定义。
首先,由于$HN$平分$\angle CHG$,且$\angle CHN = 32^\circ$,根据角平分线的定义,我们可以得出:
$\angle CHG = 2 × \angle CHN = 2 × 32^\circ = 64^\circ$,
接着,由于$AB // CD$,根据平行线的性质,我们有:
$\angle AGH = \angle CHG = 64^\circ$,(内错角相等),
最后,由于$MG \perp EF$,根据垂直的定义,我们知道$\angle MGH = 90^\circ$。
因此,我们可以求出$\angle AGM$:
$\angle AGM = 90^\circ - \angle AGH = 90^\circ - 64^\circ = 26^\circ$。
【答案】:
$26^\circ$。
13. 若∠A与∠B的两边互相平行,∠A= 40°,则∠B=
40°或140°
.答案:【解析】:
本题主要考查平行线的性质,即当两直线平行时,同位角相等,内错角相等,同旁内角互补。但在此题中,需要注意的是∠A与∠B的两边互相平行,并不意味着∠A与∠B一定是同位角或内错角,它们也有可能是同旁内角所对应的补角关系。
由于∠A与∠B的两边互相平行,所以有两种可能的关系:
1. ∠A与∠B是相等的同位角或内错角,此时∠B = ∠A = 40°。
2. ∠A与∠B是同旁内角,此时它们是互补的,即∠A + ∠B = 180°。由此可以解出∠B = 180° - 40° = 140°。
【答案】:
∠B的度数为40°或140°。
本题主要考查平行线的性质,即当两直线平行时,同位角相等,内错角相等,同旁内角互补。但在此题中,需要注意的是∠A与∠B的两边互相平行,并不意味着∠A与∠B一定是同位角或内错角,它们也有可能是同旁内角所对应的补角关系。
由于∠A与∠B的两边互相平行,所以有两种可能的关系:
1. ∠A与∠B是相等的同位角或内错角,此时∠B = ∠A = 40°。
2. ∠A与∠B是同旁内角,此时它们是互补的,即∠A + ∠B = 180°。由此可以解出∠B = 180° - 40° = 140°。
【答案】:
∠B的度数为40°或140°。
14. 如图,已知∠1= ∠BDC,∠2+∠3= 180°.
(1) 请你判断直线AD与EC的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AF交FA的延长线于点E,∠1= 70°,试求∠FAB的度数.

(1) 请你判断直线AD与EC的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AF交FA的延长线于点E,∠1= 70°,试求∠FAB的度数.

答案:(1)AD//EC,理由如下:
∵∠1=∠BDC,
∴AB//CD(同位角相等,两直线平行),
∴∠2=∠ADC(两直线平行,内错角相等),
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD//EC(同旁内角互补,两直线平行)。
(2)∵∠1=∠BDC=70°,DA平分∠BDC,
∴∠ADC=∠ADB=∠BDC/2=35°,
∵AB//CD,
∴∠2=∠ADC=35°,
∵AD//EC,CE⊥AF,
∴AD⊥AF(两直线平行,同位角相等),
∴∠FAD=90°,
∵∠FAD=∠FAB+∠2=90°,
∴∠FAB=90°-∠2=90°-35°=55°。
∵∠1=∠BDC,
∴AB//CD(同位角相等,两直线平行),
∴∠2=∠ADC(两直线平行,内错角相等),
∵∠2+∠3=180°,
∴∠ADC+∠3=180°,
∴AD//EC(同旁内角互补,两直线平行)。
(2)∵∠1=∠BDC=70°,DA平分∠BDC,
∴∠ADC=∠ADB=∠BDC/2=35°,
∵AB//CD,
∴∠2=∠ADC=35°,
∵AD//EC,CE⊥AF,
∴AD⊥AF(两直线平行,同位角相等),
∴∠FAD=90°,
∵∠FAD=∠FAB+∠2=90°,
∴∠FAB=90°-∠2=90°-35°=55°。
15. 如图,长方形纸片(对边平行)的一条边经过直角三角形纸片的直角顶点.若长方形纸片的一组对边与直角三角形纸片的两条直角边相交形成∠1和∠2,则∠2-∠1=
90°
.答案:【解析】:本题可根据平行线的性质以及直角三角形的性质来求解$\angle2 - \angle1$的值。
步骤一:利用直角三角形的性质得到相关角度关系
因为$\angle2$与$\angle3$互余(直角三角形两锐角互余,图中$\angle3$是与$\angle2$构成直角的那个锐角),$\angle1$与$\angle4$互余(图中$\angle4$是与$\angle1$构成直角的那个锐角),所以$\angle2 + \angle3 = 90^{\circ}$,$\angle1 + \angle4 = 90^{\circ}$。
步骤二:根据平行线的性质得到$\angle3$与$\angle4$的关系
已知长方形纸片的对边平行,根据“两直线平行,同位角相等”,可得$\angle3 = \angle4$。
步骤三:推导$\angle2 - \angle1$的值
由$\angle2 + \angle3 = 90^{\circ}$可得$\angle3 = 90^{\circ} - \angle2$,由$\angle1 + \angle4 = 90^{\circ}$可得$\angle4 = 90^{\circ} - \angle1$。
又因为$\angle3 = \angle4$,所以$90^{\circ} - \angle2 = 90^{\circ} - \angle1$,移项可得$\angle2 - \angle1 = 90^{\circ}$。
【答案】:$90^{\circ}$
步骤一:利用直角三角形的性质得到相关角度关系
因为$\angle2$与$\angle3$互余(直角三角形两锐角互余,图中$\angle3$是与$\angle2$构成直角的那个锐角),$\angle1$与$\angle4$互余(图中$\angle4$是与$\angle1$构成直角的那个锐角),所以$\angle2 + \angle3 = 90^{\circ}$,$\angle1 + \angle4 = 90^{\circ}$。
步骤二:根据平行线的性质得到$\angle3$与$\angle4$的关系
已知长方形纸片的对边平行,根据“两直线平行,同位角相等”,可得$\angle3 = \angle4$。
步骤三:推导$\angle2 - \angle1$的值
由$\angle2 + \angle3 = 90^{\circ}$可得$\angle3 = 90^{\circ} - \angle2$,由$\angle1 + \angle4 = 90^{\circ}$可得$\angle4 = 90^{\circ} - \angle1$。
又因为$\angle3 = \angle4$,所以$90^{\circ} - \angle2 = 90^{\circ} - \angle1$,移项可得$\angle2 - \angle1 = 90^{\circ}$。
【答案】:$90^{\circ}$
16. 如图①,已知AB//CD,∠B= 30°,∠D= 120°,∠BEF= x°,∠DFE= y°.
(1) 若x= 60,则y=
(2) 试探索x与y之间的数量关系,并说明理由;
(3) 如图②,已知EP平分∠BEF,FG平分∠DFE,反向延长FG交EP于点P,求∠P的度数.
(1) 若x= 60,则y=
90
;(2) 试探索x与y之间的数量关系,并说明理由;
解:过点E作EM//AB,过点F作FN//CD。
∵AB//CD,∴EM//FN。
∵EM//AB,∠B=30°,∴∠BEM=∠B=30°。
∵∠BEF=x°,∴∠MEF=∠BEF-∠BEM=x°-30°。
∵EM//FN,∴∠EFN=∠MEF=x°-30°。
∵FN//CD,∠D=120°,∴∠DFN=180°-∠D=60°。
∵∠DFE=y°,∠DFE=∠EFN+∠DFN,∴y=x-30+60,即x-y=-30。
∵AB//CD,∴EM//FN。
∵EM//AB,∠B=30°,∴∠BEM=∠B=30°。
∵∠BEF=x°,∴∠MEF=∠BEF-∠BEM=x°-30°。
∵EM//FN,∴∠EFN=∠MEF=x°-30°。
∵FN//CD,∠D=120°,∴∠DFN=180°-∠D=60°。
∵∠DFE=y°,∠DFE=∠EFN+∠DFN,∴y=x-30+60,即x-y=-30。
(3) 如图②,已知EP平分∠BEF,FG平分∠DFE,反向延长FG交EP于点P,求∠P的度数.
解:由(2)知x-y=-30。
∵EP平分∠BEF,∴∠PEF=∠BEF/2=x°/2。
∵FG平分∠DFE,∴∠GFE=∠DFE/2=y°/2。
∵∠P+∠PEF=∠GFE,∴∠P=∠GFE-∠PEF=(y-x)/2=15°。
∵EP平分∠BEF,∴∠PEF=∠BEF/2=x°/2。
∵FG平分∠DFE,∴∠GFE=∠DFE/2=y°/2。
∵∠P+∠PEF=∠GFE,∴∠P=∠GFE-∠PEF=(y-x)/2=15°。
答案:(1) 90
(2) 解:过点E作EM//AB,过点F作FN//CD。
∵AB//CD,∴EM//FN。
∵EM//AB,∠B=30°,∴∠BEM=∠B=30°。
∵∠BEF=x°,∴∠MEF=∠BEF-∠BEM=x°-30°。
∵EM//FN,∴∠EFN=∠MEF=x°-30°。
∵FN//CD,∠D=120°,∴∠DFN=180°-∠D=60°。
∵∠DFE=y°,∠DFE=∠EFN+∠DFN,∴y=x-30+60,即x-y=-30。
(3) 解:由(2)知x-y=-30。
∵EP平分∠BEF,∴∠PEF=∠BEF/2=x°/2。
∵FG平分∠DFE,∴∠GFE=∠DFE/2=y°/2。
∵∠P+∠PEF=∠GFE,∴∠P=∠GFE-∠PEF=(y-x)/2=15°。
(2) 解:过点E作EM//AB,过点F作FN//CD。
∵AB//CD,∴EM//FN。
∵EM//AB,∠B=30°,∴∠BEM=∠B=30°。
∵∠BEF=x°,∴∠MEF=∠BEF-∠BEM=x°-30°。
∵EM//FN,∴∠EFN=∠MEF=x°-30°。
∵FN//CD,∠D=120°,∴∠DFN=180°-∠D=60°。
∵∠DFE=y°,∠DFE=∠EFN+∠DFN,∴y=x-30+60,即x-y=-30。
(3) 解:由(2)知x-y=-30。
∵EP平分∠BEF,∴∠PEF=∠BEF/2=x°/2。
∵FG平分∠DFE,∴∠GFE=∠DFE/2=y°/2。
∵∠P+∠PEF=∠GFE,∴∠P=∠GFE-∠PEF=(y-x)/2=15°。