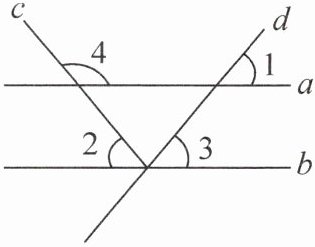
1. (2023·浙江金华)如图,已知$∠1= ∠2= ∠3= 50^{\circ }$,则$∠4$的度数是 (
A.$120^{\circ }$
B.$125^{\circ }$
C.$130^{\circ }$
D.$135^{\circ }$
C
)
A.$120^{\circ }$
B.$125^{\circ }$
C.$130^{\circ }$
D.$135^{\circ }$
答案:解:∵∠2=∠3=50°,
∴a//b(内错角相等,两直线平行),
∴∠1=∠5=50°(两直线平行,同位角相等),
∵∠4+∠5=180°(邻补角互补),
∴∠4=180°-∠5=180°-50°=130°。
答案:C
∴a//b(内错角相等,两直线平行),
∴∠1=∠5=50°(两直线平行,同位角相等),
∵∠4+∠5=180°(邻补角互补),
∴∠4=180°-∠5=180°-50°=130°。
答案:C
2. 如图,点 B,C 在直线 l 上,直线 l 外有一点 A,连接 AB,AC,$∠BAC= 45^{\circ },∠ACB$是钝角,将三角形 ABC 沿着直线 l 向右平移得到三角形$A_{1}B_{1}C_{1}$,连接$AB_{1}$.在平移的过程中,当$∠AB_{1}A_{1}= 2∠CAB_{1}$时,$∠CAB_{1}$的度数是____.


45°
答案:解:设∠CAB₁ = x,则∠AB₁A₁ = 2x。
由平移性质得:AA₁ // BB₁,AB // A₁B₁。
∴∠AB₁B = ∠B₁AA₁ = x + 45°(两直线平行,内错角相等)。
又∵∠AB₁B + ∠AB₁A₁ = 180°(平角定义),
∴x + 45° + 2x = 180°,
解得x = 45°。
∠CAB₁的度数是45°。
由平移性质得:AA₁ // BB₁,AB // A₁B₁。
∴∠AB₁B = ∠B₁AA₁ = x + 45°(两直线平行,内错角相等)。
又∵∠AB₁B + ∠AB₁A₁ = 180°(平角定义),
∴x + 45° + 2x = 180°,
解得x = 45°。
∠CAB₁的度数是45°。
3. (2025·江苏连云港期末)如图,$∠CFE+∠BDC= 180^{\circ },∠DEF= ∠B$.
(1) 若$∠CFE= 80^{\circ }$,求$∠ADC$的度数;
(2) 试判断$∠AED与∠ACB$之间的数量关系,并说明理由.

(1) 若$∠CFE= 80^{\circ }$,求$∠ADC$的度数;
(2) 试判断$∠AED与∠ACB$之间的数量关系,并说明理由.

答案:(1) 解:∵∠CFE+∠BDC=180°,∠CFE=80°
∴∠BDC=180°-80°=100°
∵∠ADC+∠BDC=180°
∴∠ADC=180°-100°=80°
(2) 解:∠AED=∠ACB,理由如下:
∵∠CFE+∠BDC=180°,∠CFE+∠DFE=180°
∴∠BDC=∠DFE
∴AB//EF
∴∠DEF=∠ADE
∵∠DEF=∠B
∴∠ADE=∠B
∴DE//BC
∴∠AED=∠ACB
∴∠BDC=180°-80°=100°
∵∠ADC+∠BDC=180°
∴∠ADC=180°-100°=80°
(2) 解:∠AED=∠ACB,理由如下:
∵∠CFE+∠BDC=180°,∠CFE+∠DFE=180°
∴∠BDC=∠DFE
∴AB//EF
∴∠DEF=∠ADE
∵∠DEF=∠B
∴∠ADE=∠B
∴DE//BC
∴∠AED=∠ACB
4. 如图,$AD// BC$,点 E 在 AD 的延长线上,$∠CDE+∠B= 180^{\circ }$.
(1) AB 与 CD 是否平行? 请说明理由;
(2) 若$∠CAF= 23^{\circ },∠1= ∠2= 2∠CAB$,求$∠CDE$的度数.

(1) AB 与 CD 是否平行? 请说明理由;
(2) 若$∠CAF= 23^{\circ },∠1= ∠2= 2∠CAB$,求$∠CDE$的度数.

答案:(1) AB//CD。证明:∵AD//BC,∴∠CDE=∠BCD(两直线平行,内错角相等)。∵∠CDE+∠B=180°,∴∠BCD+∠B=180°,∴AB//CD(同旁内角互补,两直线平行)。
(2) 解:设∠CAB=x,则∠1=∠2=2x。∵∠CAF=23°,∠1=∠CAF+∠CAE,∴2x=23°+∠CAE,∴∠CAE=2x-23°。∵AD//BC,∴∠CAD=∠2(两直线平行,内错角相等),即∠CAE+∠EAD=2x。又∵∠EAD=∠CAB=x(由(1)AB//CD,两直线平行,内错角相等),∴(2x-23°)+x=2x,解得x=23°。∴∠CAB=23°,∠2=46°。∵AB//CD,∴∠CAB=∠ACD=23°(两直线平行,内错角相等)。在△ACD中,∠DCA+∠2+∠ADC=180°,∴∠ADC=180°-23°-46°=111°。∵点E在AD延长线上,∴∠CDE=∠ADC=111°。
答:∠CDE的度数为111°。
(2) 解:设∠CAB=x,则∠1=∠2=2x。∵∠CAF=23°,∠1=∠CAF+∠CAE,∴2x=23°+∠CAE,∴∠CAE=2x-23°。∵AD//BC,∴∠CAD=∠2(两直线平行,内错角相等),即∠CAE+∠EAD=2x。又∵∠EAD=∠CAB=x(由(1)AB//CD,两直线平行,内错角相等),∴(2x-23°)+x=2x,解得x=23°。∴∠CAB=23°,∠2=46°。∵AB//CD,∴∠CAB=∠ACD=23°(两直线平行,内错角相等)。在△ACD中,∠DCA+∠2+∠ADC=180°,∴∠ADC=180°-23°-46°=111°。∵点E在AD延长线上,∴∠CDE=∠ADC=111°。
答:∠CDE的度数为111°。
5. 新素养 推理能力 如图,$AB// CD$,E 是 AB 上一点,EM 平分$∠AED$,交 CD 于点 M,且$EN⊥EM$.
(1) 若$∠EDM= 48^{\circ }$,求$∠DME$的度数;
(2) 若 MA 平分$∠CME,∠BEN= 30^{\circ }$,试说明:$MA// DE$.

(1) 若$∠EDM= 48^{\circ }$,求$∠DME$的度数;
(2) 若 MA 平分$∠CME,∠BEN= 30^{\circ }$,试说明:$MA// DE$.

答案:(1)解:∵AB//CD
∴∠AED=∠EDM=48°(两直线平行,内错角相等)
∵EM平分∠AED
∴∠DEM=∠AED/2=48°/2=24°
在△DEM中,∠DME=180°-∠EDM-∠DEM=180°-48°-24°=108°
(2)证明:∵AB//CD
∴∠AED+∠EDC=180°(两直线平行,同旁内角互补)
∵EN⊥EM
∴∠MEN=90°
∵∠BEN=30°
∴∠BEM=∠MEN+∠BEN=90°+30°=120°
∵AB为直线
∴∠AEM=180°-∠BEM=180°-120°=60°
∵EM平分∠AED
∴∠AED=2∠AEM=2×60°=120°
∴∠EDC=180°-∠AED=180°-120°=60°
由(1)知∠DME=108°
∴∠CME=180°-∠DME=180°-108°=72°
∵MA平分∠CME
∴∠CMA=∠CME/2=72°/2=36°
∵AB//CD
∴∠MAC=∠CMA=36°(两直线平行,内错角相等)
∵∠AED=120°,∠AEM=60°
∴∠DEM=60°
∠EMA=∠EMC-∠CMA=72°-36°=36°
∴∠MAC=∠EMA=36°
∴MA//DE(内错角相等,两直线平行)
∴∠AED=∠EDM=48°(两直线平行,内错角相等)
∵EM平分∠AED
∴∠DEM=∠AED/2=48°/2=24°
在△DEM中,∠DME=180°-∠EDM-∠DEM=180°-48°-24°=108°
(2)证明:∵AB//CD
∴∠AED+∠EDC=180°(两直线平行,同旁内角互补)
∵EN⊥EM
∴∠MEN=90°
∵∠BEN=30°
∴∠BEM=∠MEN+∠BEN=90°+30°=120°
∵AB为直线
∴∠AEM=180°-∠BEM=180°-120°=60°
∵EM平分∠AED
∴∠AED=2∠AEM=2×60°=120°
∴∠EDC=180°-∠AED=180°-120°=60°
由(1)知∠DME=108°
∴∠CME=180°-∠DME=180°-108°=72°
∵MA平分∠CME
∴∠CMA=∠CME/2=72°/2=36°
∵AB//CD
∴∠MAC=∠CMA=36°(两直线平行,内错角相等)
∵∠AED=120°,∠AEM=60°
∴∠DEM=60°
∠EMA=∠EMC-∠CMA=72°-36°=36°
∴∠MAC=∠EMA=36°
∴MA//DE(内错角相等,两直线平行)