1. 亮点原创 位于河南省的许昌文峰塔,又称文明寺塔,公元 1615 年由许州知州郑振光倡导创建,为八角十三层仿木楼阁式砖塔,平面呈正八边形,是第六批全国重点文物保护单位. 下列图形是正八边形的为(
]
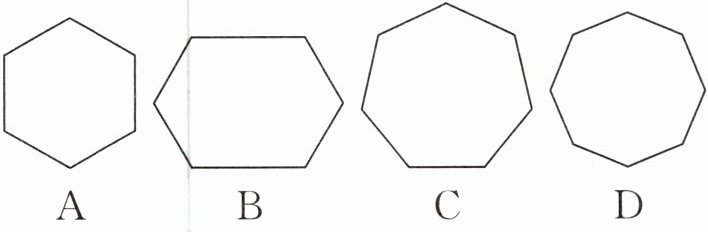
D
)]

答案:D
2. (2025·江苏徐州期末)某多边形由一个顶点引出的对角线可以将该多边形分成 10 个三角形,则这个多边形的边数是(
A.11
B.12
C.13
D.14
B
)A.11
B.12
C.13
D.14
答案:【解析】:
首先,我们需要理解多边形由一个顶点引出的对角线可以将多边形分成多少个三角形。
对于一个$n$边形,从一个顶点引出的对角线数量是$n-3$(因为与该顶点相邻的两个顶点和该顶点自身不能作为对角线的终点)。
这些对角线将多边形分成$n-2$个三角形。
题目给出,这些对角线将多边形分成了10个三角形,所以我们有方程:
$n - 2 = 10$
解这个方程,我们得到:
$n = 12$
所以,这个多边形的边数是12。
【答案】:B.12。
首先,我们需要理解多边形由一个顶点引出的对角线可以将多边形分成多少个三角形。
对于一个$n$边形,从一个顶点引出的对角线数量是$n-3$(因为与该顶点相邻的两个顶点和该顶点自身不能作为对角线的终点)。
这些对角线将多边形分成$n-2$个三角形。
题目给出,这些对角线将多边形分成了10个三角形,所以我们有方程:
$n - 2 = 10$
解这个方程,我们得到:
$n = 12$
所以,这个多边形的边数是12。
【答案】:B.12。
3. (教材 P195 练习 2 变式)任意七边形都有
14
条对角线.答案:【解析】:
对于一个n边形,每个顶点都可以与其他$n-1$个顶点相连,但其中$2$个连接是与相邻的顶点,所以每个顶点可以形成$n-3$条对角线。由于n边形有n个顶点,所以总共可以形成$n(n-3)$条对角线,但每条对角线被计算了两次(两个端点都可以作为起点),所以n边形的对角线数量为$\frac{n(n-3)}{2}$。
将$n=7$代入上述公式,得到七边形的对角线数量为:
$\frac{7×(7-3)}{2}=\frac{7×4}{2}=14$。
【答案】:
14
对于一个n边形,每个顶点都可以与其他$n-1$个顶点相连,但其中$2$个连接是与相邻的顶点,所以每个顶点可以形成$n-3$条对角线。由于n边形有n个顶点,所以总共可以形成$n(n-3)$条对角线,但每条对角线被计算了两次(两个端点都可以作为起点),所以n边形的对角线数量为$\frac{n(n-3)}{2}$。
将$n=7$代入上述公式,得到七边形的对角线数量为:
$\frac{7×(7-3)}{2}=\frac{7×4}{2}=14$。
【答案】:
14
4. 新趋势 推导探究 如图,从一个多边形的某一条边上的一点(不与端点重合)出发,分别连接这个点与其他所有顶点,可以把这个多边形分割成若干个三角形. 以三角形、四边形、五边形为例,你能总结出什么规律?
]

]

答案:解:
三角形:从一条边上一点出发,可分割成1个三角形,1=3-2;
四边形:从一条边上一点出发,可分割成2个三角形,2=4-2;
五边形:从一条边上一点出发,可分割成3个三角形,3=5-2;
规律:从n边形某条边上一点(不与端点重合)出发,连接其他顶点,可分割成(n-2)个三角形。
三角形:从一条边上一点出发,可分割成1个三角形,1=3-2;
四边形:从一条边上一点出发,可分割成2个三角形,2=4-2;
五边形:从一条边上一点出发,可分割成3个三角形,3=5-2;
规律:从n边形某条边上一点(不与端点重合)出发,连接其他顶点,可分割成(n-2)个三角形。
5. 对角线是 5 条的多边形为(
A.四边形
B.五边形
C.六边形
D.七边形
B
)A.四边形
B.五边形
C.六边形
D.七边形
答案:【解析】:
题目要求确定对角线数量为5条的多边形的边数。我们知道,一个n边形的对角线数量可以通过公式$\frac{n(n-3)}{2}$来计算。
对于四边形,其对角线数量为$\frac{4(4-3)}{2}=2$,不符合题意;
对于五边形,其对角线数量为$\frac{5(5-3)}{2}=5$,符合题意;
对于六边形,其对角线数量为$\frac{6(6-3)}{2}=9$,不符合题意;
对于七边形,其对角线数量为$\frac{7(7-3)}{2}=14$,不符合题意。
因此,对角线是5条的多边形为五边形。
【答案】:
B.五边形。
题目要求确定对角线数量为5条的多边形的边数。我们知道,一个n边形的对角线数量可以通过公式$\frac{n(n-3)}{2}$来计算。
对于四边形,其对角线数量为$\frac{4(4-3)}{2}=2$,不符合题意;
对于五边形,其对角线数量为$\frac{5(5-3)}{2}=5$,符合题意;
对于六边形,其对角线数量为$\frac{6(6-3)}{2}=9$,不符合题意;
对于七边形,其对角线数量为$\frac{7(7-3)}{2}=14$,不符合题意。
因此,对角线是5条的多边形为五边形。
【答案】:
B.五边形。
6. 若从多边形纸片中剪去一个三角形,剩余的部分是一个四边形,则原多边形纸片的边数是
3或4或5
.答案:解:分三种情况讨论:
1. 若沿对角线剪去一个三角形,原多边形边数比剩余四边形边数多1,即原多边形边数为4+1=5;
2. 若从一个顶点和相邻边上一点剪去一个三角形,原多边形边数与剩余四边形边数相等,即原多边形边数为4;
3. 若从相邻两边上各取一点剪去一个三角形,原多边形边数比剩余四边形边数少1,即原多边形边数为4-1=3。
综上,原多边形纸片的边数是3或4或5。
答案:3或4或5
1. 若沿对角线剪去一个三角形,原多边形边数比剩余四边形边数多1,即原多边形边数为4+1=5;
2. 若从一个顶点和相邻边上一点剪去一个三角形,原多边形边数与剩余四边形边数相等,即原多边形边数为4;
3. 若从相邻两边上各取一点剪去一个三角形,原多边形边数比剩余四边形边数少1,即原多边形边数为4-1=3。
综上,原多边形纸片的边数是3或4或5。
答案:3或4或5
7. 如图,在$\triangle ABC$中,$∠A= 45^{\circ}$,外角$∠ACD= 100^{\circ}$,求$∠B和∠ACB$的大小.
]

]

答案:【解析】:本题主要考查三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角之和。我们可以利用这一性质求出$∠B$的度数,再根据平角的定义求出$∠ACB$的度数。
【答案】:
解:
∵$∠ACD$是$\triangle ABC$的一个外角,
∴根据三角形外角的性质可得$∠ACD = ∠A + ∠B$。
已知$∠A = 45^{\circ}$,$∠ACD = 100^{\circ}$,
则$∠B = ∠ACD - ∠A = 100^{\circ} - 45^{\circ} = 55^{\circ}$。
∵$∠ACB$与$∠ACD$组成一个平角,平角为$180^{\circ}$,
∴$∠ACB = 180^{\circ} - ∠ACD = 180^{\circ} - 100^{\circ} = 80^{\circ}$。
综上,$∠B$的大小为$55^{\circ}$,$∠ACB$的大小为$80^{\circ}$。
【答案】:
解:
∵$∠ACD$是$\triangle ABC$的一个外角,
∴根据三角形外角的性质可得$∠ACD = ∠A + ∠B$。
已知$∠A = 45^{\circ}$,$∠ACD = 100^{\circ}$,
则$∠B = ∠ACD - ∠A = 100^{\circ} - 45^{\circ} = 55^{\circ}$。
∵$∠ACB$与$∠ACD$组成一个平角,平角为$180^{\circ}$,
∴$∠ACB = 180^{\circ} - ∠ACD = 180^{\circ} - 100^{\circ} = 80^{\circ}$。
综上,$∠B$的大小为$55^{\circ}$,$∠ACB$的大小为$80^{\circ}$。
8. 在$n$边形内(不包括边上)任取一点,把这个点与$n$边形各顶点分别连接可得到的三角形的个数为
$n$
.答案:【解析】:
这个问题主要考察的是多边形和三角形的性质以及组合数学的应用。题目要求我们在一个n边形内部任意取一点,并将这个点与n边形的各个顶点连接,然后计算可以形成多少个三角形。
首先,我们明确三角形是由三条边和三个顶点构成的。在这个问题中,我们已经有了n边形的各顶点和一个在多边形内部的任意点。通过将这个内部点与n边形的每一个顶点连接,我们可以形成n条线段。
接下来,我们需要考虑如何由这些线段构成三角形。由于内部点已经与每一个顶点连接,因此每三条从内部点出发到不同顶点的线段,都会与n边形的一条边构成一个三角形。换句话说,从内部点出发的每一条线段都可以作为三角形的一条边。
因为我们需要从n条线段中选择3条来构成一个三角形,但实际上,由于内部点已经确定,我们只需要选择n边形的一个顶点,就能唯一确定一个三角形(由内部点和该顶点以及该顶点的相邻两个顶点构成)。因此,对于n边形的每一个顶点,我们都可以得到一个唯一的三角形。
所以,总共可以得到的三角形个数就是n边形的顶点数,即n。
【答案】:
$n$
这个问题主要考察的是多边形和三角形的性质以及组合数学的应用。题目要求我们在一个n边形内部任意取一点,并将这个点与n边形的各个顶点连接,然后计算可以形成多少个三角形。
首先,我们明确三角形是由三条边和三个顶点构成的。在这个问题中,我们已经有了n边形的各顶点和一个在多边形内部的任意点。通过将这个内部点与n边形的每一个顶点连接,我们可以形成n条线段。
接下来,我们需要考虑如何由这些线段构成三角形。由于内部点已经与每一个顶点连接,因此每三条从内部点出发到不同顶点的线段,都会与n边形的一条边构成一个三角形。换句话说,从内部点出发的每一条线段都可以作为三角形的一条边。
因为我们需要从n条线段中选择3条来构成一个三角形,但实际上,由于内部点已经确定,我们只需要选择n边形的一个顶点,就能唯一确定一个三角形(由内部点和该顶点以及该顶点的相邻两个顶点构成)。因此,对于n边形的每一个顶点,我们都可以得到一个唯一的三角形。
所以,总共可以得到的三角形个数就是n边形的顶点数,即n。
【答案】:
$n$
9. (1)【探究】
① 画出下列多边形的所有对角线;

② 根据所画图形,填表:
|从一个顶点出发画的对角线条数|1|
|多边形总的对角线条数(列式表示)|$\frac{4×1}{2}$|
(2)【猜想】
① 从一百边形的一个顶点出发可以画
② 从$n$边形的一个顶点出发可以画
① 画出下列多边形的所有对角线;

② 根据所画图形,填表:
|从一个顶点出发画的对角线条数|1|
2
|3
||多边形总的对角线条数(列式表示)|$\frac{4×1}{2}$|
$\frac{5×2}{2}$
|$\frac{6×3}{2}$
|(2)【猜想】
① 从一百边形的一个顶点出发可以画
97
条对角线,一百边形共有4850
条对角线;② 从$n$边形的一个顶点出发可以画
$(n - 3)$
条对角线,$n$边形共有$\frac{n(n - 3)}{2}$
条对角线.答案:【解析】:
本题主要考查多边形对角线的相关知识,需要先通过画出不同多边形的对角线,找出规律,再根据规律进行猜想。
对于(1)①,需要画出四边形、五边形、六边形的所有对角线。
四边形:从四边形的一个顶点出发,只能画$1$条对角线(因为与自身和相邻的两个顶点不能连对角线),四边形总共有$\frac{4×(4 - 3)}{2}=\frac{4×1}{2}=2$条对角线。
五边形:从五边形的一个顶点出发,能画$2$条对角线(除去自身和相邻的两个顶点),五边形总共有$\frac{5×(5 - 3)}{2}=\frac{5×2}{2}=5$条对角线。
六边形:从六边形的一个顶点出发,能画$3$条对角线(除去自身和相邻的两个顶点),六边形总共有$\frac{6×(6 - 3)}{2}=\frac{6×3}{2}=9$条对角线。
对于(1)②,根据上述计算结果填表:
从一个顶点出发画的对角线条数:四边形是$1$,五边形是$2$,六边形是$3$。
多边形总的对角线条数(列式表示):四边形是$\frac{4×1}{2}$,五边形是$\frac{5×2}{2}$,六边形是$\frac{6×3}{2}$。
对于(2)①,从一百边形的一个顶点出发,因为不能和自身以及相邻的两个顶点连对角线,所以可以画$100 - 3 = 97$条对角线。
一百边形总的对角线条数,根据前面的规律,可列式为$\frac{100×(100 - 3)}{2}=\frac{100×97}{2}=4850$条。
对于(2)②,从$n$边形的一个顶点出发,同样不能和自身以及相邻的两个顶点连对角线,所以可以画$(n - 3)$条对角线。
$n$边形总的对角线条数,根据前面的规律,可列式为$\frac{n(n - 3)}{2}$条。
【答案】:
(1)①图略(按照上述分析画出四边形、五边形、六边形的所有对角线即可);
②
|从一个顶点出发画的对角线条数|1|2|3|
| ---- | ---- | ---- | ---- |
|多边形总的对角线条数(列式表示)|$\frac{4×1}{2}$|$\frac{5×2}{2}$|$\frac{6×3}{2}$|
(2)①$97$;$4850$;
②$(n - 3)$;$\frac{n(n - 3)}{2}$。
本题主要考查多边形对角线的相关知识,需要先通过画出不同多边形的对角线,找出规律,再根据规律进行猜想。
对于(1)①,需要画出四边形、五边形、六边形的所有对角线。
四边形:从四边形的一个顶点出发,只能画$1$条对角线(因为与自身和相邻的两个顶点不能连对角线),四边形总共有$\frac{4×(4 - 3)}{2}=\frac{4×1}{2}=2$条对角线。
五边形:从五边形的一个顶点出发,能画$2$条对角线(除去自身和相邻的两个顶点),五边形总共有$\frac{5×(5 - 3)}{2}=\frac{5×2}{2}=5$条对角线。
六边形:从六边形的一个顶点出发,能画$3$条对角线(除去自身和相邻的两个顶点),六边形总共有$\frac{6×(6 - 3)}{2}=\frac{6×3}{2}=9$条对角线。
对于(1)②,根据上述计算结果填表:
从一个顶点出发画的对角线条数:四边形是$1$,五边形是$2$,六边形是$3$。
多边形总的对角线条数(列式表示):四边形是$\frac{4×1}{2}$,五边形是$\frac{5×2}{2}$,六边形是$\frac{6×3}{2}$。
对于(2)①,从一百边形的一个顶点出发,因为不能和自身以及相邻的两个顶点连对角线,所以可以画$100 - 3 = 97$条对角线。
一百边形总的对角线条数,根据前面的规律,可列式为$\frac{100×(100 - 3)}{2}=\frac{100×97}{2}=4850$条。
对于(2)②,从$n$边形的一个顶点出发,同样不能和自身以及相邻的两个顶点连对角线,所以可以画$(n - 3)$条对角线。
$n$边形总的对角线条数,根据前面的规律,可列式为$\frac{n(n - 3)}{2}$条。
【答案】:
(1)①图略(按照上述分析画出四边形、五边形、六边形的所有对角线即可);
②
|从一个顶点出发画的对角线条数|1|2|3|
| ---- | ---- | ---- | ---- |
|多边形总的对角线条数(列式表示)|$\frac{4×1}{2}$|$\frac{5×2}{2}$|$\frac{6×3}{2}$|
(2)①$97$;$4850$;
②$(n - 3)$;$\frac{n(n - 3)}{2}$。