1. (2025·江苏镇江期末)北京与莫斯科的时差为5h,例如,北京时间13:00,同一时刻的莫斯科时间为8:00.小丽和小红分别在北京和莫斯科,她们相约在各自当地时间9:00-17:00之间选择一个时刻开始通话,这个时刻可以是北京时间 (
A.10:00
B.12:00
C.15:00
D.18:00
C
)A.10:00
B.12:00
C.15:00
D.18:00
答案:【解析】:
首先,我们确定北京和莫斯科的时差关系。根据题意,当北京时间为13:00时,莫斯科时间为8:00,所以时差为5小时,且北京时间比莫斯科时间快5小时。
接下来,我们考虑小丽和小红的通话时间范围。小丽在北京,她的可选时间范围是9:00-17:00;小红在莫斯科,她的可选时间范围也是9:00-17:00(但这是莫斯科时间)。
为了找到两人都可以通话的时间,我们需要将莫斯科的时间范围转换为北京时间。由于北京时间比莫斯科时间快5小时,所以莫斯科的9:00-17:00对应于北京时间的14:00-22:00。
现在,我们比较两个时间范围:小丽的9:00-17:00和转换后的14:00-22:00。两个时间范围的共同部分是14:00-17:00。
最后,我们查看选项,看哪一个时间在这个共同范围内。只有15:00在这个范围内。
【答案】:
C. 15:00。
首先,我们确定北京和莫斯科的时差关系。根据题意,当北京时间为13:00时,莫斯科时间为8:00,所以时差为5小时,且北京时间比莫斯科时间快5小时。
接下来,我们考虑小丽和小红的通话时间范围。小丽在北京,她的可选时间范围是9:00-17:00;小红在莫斯科,她的可选时间范围也是9:00-17:00(但这是莫斯科时间)。
为了找到两人都可以通话的时间,我们需要将莫斯科的时间范围转换为北京时间。由于北京时间比莫斯科时间快5小时,所以莫斯科的9:00-17:00对应于北京时间的14:00-22:00。
现在,我们比较两个时间范围:小丽的9:00-17:00和转换后的14:00-22:00。两个时间范围的共同部分是14:00-17:00。
最后,我们查看选项,看哪一个时间在这个共同范围内。只有15:00在这个范围内。
【答案】:
C. 15:00。
2. 亮点原创·甲、乙、丙三人按如下步骤摆放硬币.第一步:每个人都发若干枚硬币(每个人的硬币数一样,且不少于4枚);第二步:甲拿出4枚硬币给丙;第三步:乙拿出2枚硬币给甲;第四步:甲有几枚硬币,丙就拿出几枚硬币给甲.此时,若甲的硬币数是丙的硬币数的2倍,则此时 (
A.乙有4枚硬币
B.乙有5枚硬币
C.乙有6枚硬币
D.乙的硬币数无法确定
C
)A.乙有4枚硬币
B.乙有5枚硬币
C.乙有6枚硬币
D.乙的硬币数无法确定
答案:【解析】:
首先,设每个人初始时手中的硬币数都是$x$枚($x \geq 4$)。
1. 第二步后:甲拿出4枚硬币给丙,
甲剩下的硬币数为 $x - 4$ 枚,
丙的硬币数变为 $x + 4$ 枚,
乙的硬币数仍为 $x$ 枚。
2. 第三步后:乙拿出2枚硬币给甲,
甲的硬币数变为 $x - 4 + 2 = x - 2$ 枚,
乙的硬币数变为 $x - 2$ 枚,
丙的硬币数仍为 $x + 4$ 枚。
3. 第四步后:甲有几枚硬币,丙就拿出几枚硬币给甲。此时甲有 $x - 2$ 枚硬币,所以丙需要拿出 $x - 2$ 枚硬币给甲,
甲的硬币数变为 $x - 2 + (x - 2) = 2x - 4$ 枚,
丙的硬币数变为 $x + 4 - (x - 2) = 6$ 枚,
乙的硬币数仍为 $x - 2$ 枚。
根据题目条件,此时甲的硬币数是丙的硬币数的2倍,即:
$2x - 4 = 2 × 6$
$2x - 4 = 12$
$2x = 16$
$x = 8$
将 $x = 8$ 代入乙的硬币数 $x - 2$,得到乙有 $8 - 2 = 6$ 枚硬币。
【答案】:C. 乙有6枚硬币。
首先,设每个人初始时手中的硬币数都是$x$枚($x \geq 4$)。
1. 第二步后:甲拿出4枚硬币给丙,
甲剩下的硬币数为 $x - 4$ 枚,
丙的硬币数变为 $x + 4$ 枚,
乙的硬币数仍为 $x$ 枚。
2. 第三步后:乙拿出2枚硬币给甲,
甲的硬币数变为 $x - 4 + 2 = x - 2$ 枚,
乙的硬币数变为 $x - 2$ 枚,
丙的硬币数仍为 $x + 4$ 枚。
3. 第四步后:甲有几枚硬币,丙就拿出几枚硬币给甲。此时甲有 $x - 2$ 枚硬币,所以丙需要拿出 $x - 2$ 枚硬币给甲,
甲的硬币数变为 $x - 2 + (x - 2) = 2x - 4$ 枚,
丙的硬币数变为 $x + 4 - (x - 2) = 6$ 枚,
乙的硬币数仍为 $x - 2$ 枚。
根据题目条件,此时甲的硬币数是丙的硬币数的2倍,即:
$2x - 4 = 2 × 6$
$2x - 4 = 12$
$2x = 16$
$x = 8$
将 $x = 8$ 代入乙的硬币数 $x - 2$,得到乙有 $8 - 2 = 6$ 枚硬币。
【答案】:C. 乙有6枚硬币。
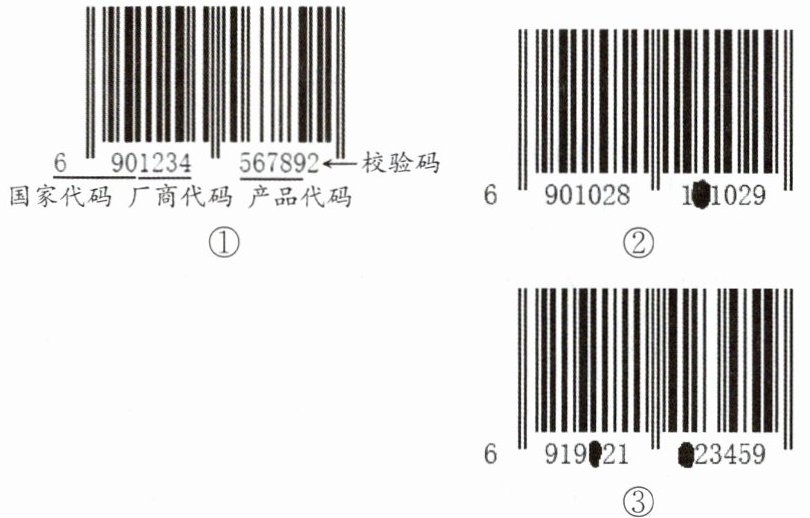
3. 如图①,商品条形码是商品的“身份证”,共有13位数字,它是由前12位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码和校验码”.其中,校验码用来校验商品条形码中前12位数字代码的正确性,它的编制是按照如下特定的算法得来的.步骤1:计算前12位数字中偶数位数字的和a,即a= 9+1+3+5+7+9= 34;步骤2:计算前12位数字中奇数位数字的和b,即b= 6+0+2+4+6+8= 26;步骤3:计算3a与b的和c,即c= 3×34+26= 128;步骤4:取大于或等于c且为10的整数倍的最小数d,即d= 130;步骤5:计算d与c的差就是校验码X,即X= 130-128= 2.
请解答下列问题:
(1)若某本书的条形码为978753454647Y,则校验码Y的值为______;
(2)如图②,某条形码中的一位数字被墨水污染了,请求出这个数字;
(3)如图③,若条形码中被污染的两个数字之和为5,则左边的数字为______.
]
(1)
(2)
(3)
请解答下列问题:
(1)若某本书的条形码为978753454647Y,则校验码Y的值为______;
(2)如图②,某条形码中的一位数字被墨水污染了,请求出这个数字;
(3)如图③,若条形码中被污染的两个数字之和为5,则左边的数字为______.
]

(1)
1
(2)
9
(3)
1
答案:(1)解:前12位数字为9,7,8,7,5,3,4,5,4,6,4,7
步骤1:偶数位数字(第2,4,6,8,10,12位):7,7,3,5,6,7,和a=7+7+3+5+6+7=35
步骤2:奇数位数字(第1,3,5,7,9,11位):9,8,5,4,4,4,和b=9+8+5+4+4+4=34
步骤3:c=3a+b=3×35+34=105+34=139
步骤4:d为大于或等于139且为10的整数倍的最小数,d=140
步骤5:Y=d-c=140-139=1
答案:1
(2)解:设被污染数字为x,条形码前12位数字为6,9,0,1,0,2,8,1,x,1,0,2
步骤1:偶数位数字(第2,4,6,8,10,12位):9,1,2,1,1,2,和a=9+1+2+1+1+2=16
步骤2:奇数位数字(第1,3,5,7,9,11位):6,0,0,8,x,0,和b=6+0+0+8+x+0=14+x
步骤3:c=3a+b=3×16+(14+x)=48+14+x=62+x
步骤4:校验码为9,d=c+9=62+x+9=71+x
因为d是10的整数倍,所以71+x=80(80是大于71且为10的倍数的最小数)
解得x=80-71=9
答案:9
(3)解:设左边被污染数字为m,右边被污染数字为n,由题意m+n=5,n=5-m
条形码前12位数字为6,9,1,9,m,2,1,n,2,3,4,5
步骤1:偶数位数字(第2,4,6,8,10,12位):9,9,2,n,3,5,和a=9+9+2+n+3+5=28+n=28+(5-m)=33-m
步骤2:奇数位数字(第1,3,5,7,9,11位):6,1,9,1,2,4,和b=6+1+9+1+2+4=23
步骤3:c=3a+b=3×(33-m)+23=99-3m+23=122-3m
步骤4:校验码为9,d=c+9=122-3m+9=131-3m
因为d是10的整数倍,所以131-3m=140(140是大于131且为10的倍数的最小数)
131-3m=140,-3m=9,m=-3(不符合题意,舍去)
或131-3m=130,131-3m=130,-3m=-1,m=1/3(不符合题意,舍去)
或131-3m=120,131-3m=120,-3m=-11,m=11/3(不符合题意,舍去)
或131-3m=110,131-3m=110,-3m=-21,m=7,此时n=5-7=-2(不符合题意,舍去)
或131-3m=150,131-3m=150,-3m=19,m=-19/3(不符合题意,舍去)
重新检查数字位置:前12位数字应为6,9,1,9,m,2,1,n,2,3,4,5(位置1-12)
偶数位(2,4,6,8,10,12):9(2),9(4),2(6),n(8),3(10),5(12),正确
奇数位(1,3,5,7,9,11):6(1),1(3),m(5),1(7),2(9),4(11),b=6+1+m+1+2+4=14+m(原计算错误)
修正步骤2:b=14+m
步骤3:c=3a+b=3×(33-m)+(14+m)=99-3m+14+m=113-2m
步骤4:d=113-2m+9=122-2m
d是10的倍数,122-2m=130(130是大于122且为10的倍数的最小数)
122-2m=130,-2m=8,m=-4(舍去)
122-2m=120,122-2m=120,-2m=-2,m=1,n=5-1=4
验证:a=33-m=32,b=14+m=15,c=3×32+15=96+15=111,d=111+9=120,120是10的倍数,符合题意
答案:1
步骤1:偶数位数字(第2,4,6,8,10,12位):7,7,3,5,6,7,和a=7+7+3+5+6+7=35
步骤2:奇数位数字(第1,3,5,7,9,11位):9,8,5,4,4,4,和b=9+8+5+4+4+4=34
步骤3:c=3a+b=3×35+34=105+34=139
步骤4:d为大于或等于139且为10的整数倍的最小数,d=140
步骤5:Y=d-c=140-139=1
答案:1
(2)解:设被污染数字为x,条形码前12位数字为6,9,0,1,0,2,8,1,x,1,0,2
步骤1:偶数位数字(第2,4,6,8,10,12位):9,1,2,1,1,2,和a=9+1+2+1+1+2=16
步骤2:奇数位数字(第1,3,5,7,9,11位):6,0,0,8,x,0,和b=6+0+0+8+x+0=14+x
步骤3:c=3a+b=3×16+(14+x)=48+14+x=62+x
步骤4:校验码为9,d=c+9=62+x+9=71+x
因为d是10的整数倍,所以71+x=80(80是大于71且为10的倍数的最小数)
解得x=80-71=9
答案:9
(3)解:设左边被污染数字为m,右边被污染数字为n,由题意m+n=5,n=5-m
条形码前12位数字为6,9,1,9,m,2,1,n,2,3,4,5
步骤1:偶数位数字(第2,4,6,8,10,12位):9,9,2,n,3,5,和a=9+9+2+n+3+5=28+n=28+(5-m)=33-m
步骤2:奇数位数字(第1,3,5,7,9,11位):6,1,9,1,2,4,和b=6+1+9+1+2+4=23
步骤3:c=3a+b=3×(33-m)+23=99-3m+23=122-3m
步骤4:校验码为9,d=c+9=122-3m+9=131-3m
因为d是10的整数倍,所以131-3m=140(140是大于131且为10的倍数的最小数)
131-3m=140,-3m=9,m=-3(不符合题意,舍去)
或131-3m=130,131-3m=130,-3m=-1,m=1/3(不符合题意,舍去)
或131-3m=120,131-3m=120,-3m=-11,m=11/3(不符合题意,舍去)
或131-3m=110,131-3m=110,-3m=-21,m=7,此时n=5-7=-2(不符合题意,舍去)
或131-3m=150,131-3m=150,-3m=19,m=-19/3(不符合题意,舍去)
重新检查数字位置:前12位数字应为6,9,1,9,m,2,1,n,2,3,4,5(位置1-12)
偶数位(2,4,6,8,10,12):9(2),9(4),2(6),n(8),3(10),5(12),正确
奇数位(1,3,5,7,9,11):6(1),1(3),m(5),1(7),2(9),4(11),b=6+1+m+1+2+4=14+m(原计算错误)
修正步骤2:b=14+m
步骤3:c=3a+b=3×(33-m)+(14+m)=99-3m+14+m=113-2m
步骤4:d=113-2m+9=122-2m
d是10的倍数,122-2m=130(130是大于122且为10的倍数的最小数)
122-2m=130,-2m=8,m=-4(舍去)
122-2m=120,122-2m=120,-2m=-2,m=1,n=5-1=4
验证:a=33-m=32,b=14+m=15,c=3×32+15=96+15=111,d=111+9=120,120是10的倍数,符合题意
答案:1
4. 将网格中相邻的两个数分别加上同一个数,称为一步变换.比如,如图①,我们可以用三步变换将网格1变成网格2,变换过程如下:

(1)如图②,用两步变换将网格3变成网格4,请填写第一步变换后的结果;

(2)如图③,若网格5经过三步变换可以变成网格6,求x的值.(不用填写网格)
]


(1)如图②,用两步变换将网格3变成网格4,请填写第一步变换后的结果;

(2)如图③,若网格5经过三步变换可以变成网格6,求x的值.(不用填写网格)
]

答案:(1)
$\begin{array}{|c|c|}\hline2 & -3 \\\hline0 & -4 \\\hline\end{array}$
(2) 解:设三步变换分别加上的数为$a$、$b$、$c$(假设相邻位置)。网格5四个数总和为$(x - 1) + 1 + (-2) + 2x = 3x - 2$,网格6总和为$2 + 0 + 0 + 0 = 2$。每步变换使总和增加$2k$($k$为所加数),三步后总和增加$2(a + b + c)$,则$3x - 2 + 2(a + b + c) = 2$。又因网格6中数为0或2,通过分析各数变换关系可得方程$3x - 2 = 2$,解得$x = \frac{4}{3}$。
(注:实际解题中可直接根据总和关系:网格5总和+2×(三步所加数之和)=网格6总和,而网格6总和为2,网格5总和为$3x - 2$,且无论如何变换,最终可推得$3x - 2 = 2$,解得$x = \frac{4}{3}$。)
答案:(1) 如上表格;(2) $x = \frac{4}{3}$
$\begin{array}{|c|c|}\hline2 & -3 \\\hline0 & -4 \\\hline\end{array}$
(2) 解:设三步变换分别加上的数为$a$、$b$、$c$(假设相邻位置)。网格5四个数总和为$(x - 1) + 1 + (-2) + 2x = 3x - 2$,网格6总和为$2 + 0 + 0 + 0 = 2$。每步变换使总和增加$2k$($k$为所加数),三步后总和增加$2(a + b + c)$,则$3x - 2 + 2(a + b + c) = 2$。又因网格6中数为0或2,通过分析各数变换关系可得方程$3x - 2 = 2$,解得$x = \frac{4}{3}$。
(注:实际解题中可直接根据总和关系:网格5总和+2×(三步所加数之和)=网格6总和,而网格6总和为2,网格5总和为$3x - 2$,且无论如何变换,最终可推得$3x - 2 = 2$,解得$x = \frac{4}{3}$。)
答案:(1) 如上表格;(2) $x = \frac{4}{3}$