1. 生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例如:$12= 1×10+2$,$212= 2×10×10+1×10+2$;计算机也常用十六进制来表示字符代码,它是用0~F来表示0~15,满十六进一,它与十进制对应的数如下表:
|十进制|0|1|2|…|8|9|10|11|12|13|14|15|16|17|…|
|十六进制|0|1|2|…|8|9|A|B|C|D|E|F|10|11|…|
例如:十六进制数2B对应十进制的数为$2×16+11= 43$,10C对应十进制的数为$1×16×16+0×16+12= 268$,那么14E对应十进制的数为(
A.28
B.62
C.238
D.334
|十进制|0|1|2|…|8|9|10|11|12|13|14|15|16|17|…|
|十六进制|0|1|2|…|8|9|A|B|C|D|E|F|10|11|…|
例如:十六进制数2B对应十进制的数为$2×16+11= 43$,10C对应十进制的数为$1×16×16+0×16+12= 268$,那么14E对应十进制的数为(
D
)A.28
B.62
C.238
D.334
答案:【解析】:
题目考查了十六进制与十进制之间的转换。
根据题目中给出的十六进制与十进制转换的规则,需要将十六进制的每一位与16的相应次方相乘,然后求和。
对于十六进制数$14E$,可以将其拆分为1、4和E(E在十六进制中表示14),然后按照规则进行计算:
$1 × 16^2 + 4 × 16^1 + 14 × 16^0$
$= 1 × 256 + 4 × 16 + 14 × 1$
$= 256 + 64 + 14$
$= 334$
【答案】:
D. 334。
题目考查了十六进制与十进制之间的转换。
根据题目中给出的十六进制与十进制转换的规则,需要将十六进制的每一位与16的相应次方相乘,然后求和。
对于十六进制数$14E$,可以将其拆分为1、4和E(E在十六进制中表示14),然后按照规则进行计算:
$1 × 16^2 + 4 × 16^1 + 14 × 16^0$
$= 1 × 256 + 4 × 16 + 14 × 1$
$= 256 + 64 + 14$
$= 334$
【答案】:
D. 334。
|日常语言|代数语言|
|连云港到南京的城际列车在连云港站出发时车上有一些乘客|x|
|到灌云站时无人下车,有10人上车|x+10|
|到灌南站时有1人下车,后来又上来车上人数的$\frac{1}{9}$|
|连云港到南京的城际列车在连云港站出发时车上有一些乘客|x|
|到灌云站时无人下车,有10人上车|x+10|
|到灌南站时有1人下车,后来又上来车上人数的$\frac{1}{9}$|
$\frac{10}{9}x + 10$
|答案:解:到灌南站时有1人下车后车上人数为:$x + 10 - 1 = x + 9$
后来又上来车上人数的$\frac{1}{9}$,则上车人数为:$\frac{1}{9}(x + 9)$
此时车上总人数为:$(x + 9) + \frac{1}{9}(x + 9) = (x + 9)\left(1 + \frac{1}{9}\right) = (x + 9)×\frac{10}{9} = \frac{10}{9}x + 10$
$\frac{10}{9}x + 10$
后来又上来车上人数的$\frac{1}{9}$,则上车人数为:$\frac{1}{9}(x + 9)$
此时车上总人数为:$(x + 9) + \frac{1}{9}(x + 9) = (x + 9)\left(1 + \frac{1}{9}\right) = (x + 9)×\frac{10}{9} = \frac{10}{9}x + 10$
$\frac{10}{9}x + 10$
3. 【阅读理解】
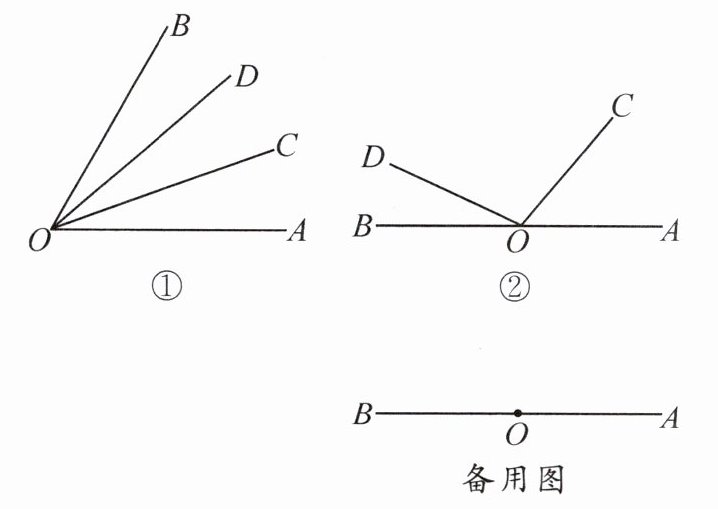
射线OC是$∠AOB$内部的一条射线,若$∠AOC= \frac{1}{2}∠BOC$,则我们称射线OC是射线OA的伴随线. 如图①,$∠AOB= 60^{\circ}$,$∠AOC= ∠COD= ∠BOD= 20^{\circ}$,则$∠AOC= \frac{1}{2}∠BOC$,称射线OC是射线OA的伴随线;同时,由于$∠BOD= \frac{1}{2}∠AOD$,称射线OD是射线OB的伴随线.
【知识运用】
如图②,$∠AOB= 180^{\circ}$,射线OC与射线OA重合,并绕点O以每秒$6^{\circ}$的速度逆时针旋转;射线OD与射线OB重合,并绕点O以每秒$3^{\circ}$的速度顺时针旋转. 射线OC与射线OD同时开始旋转,当射线OC与射线OB重合时,整个运动停止. 设运动的时间为t s.
(1)是否存在某个时刻,使得$∠COD的度数是45^{\circ}$?若存在,求出t的值;若不存在,请说明理由;
(2)当t为何值时,射线OB,OC,OD中恰好有一条射线是其余两条射线中某一条射线的伴随线?
射线OC是$∠AOB$内部的一条射线,若$∠AOC= \frac{1}{2}∠BOC$,则我们称射线OC是射线OA的伴随线. 如图①,$∠AOB= 60^{\circ}$,$∠AOC= ∠COD= ∠BOD= 20^{\circ}$,则$∠AOC= \frac{1}{2}∠BOC$,称射线OC是射线OA的伴随线;同时,由于$∠BOD= \frac{1}{2}∠AOD$,称射线OD是射线OB的伴随线.
【知识运用】
如图②,$∠AOB= 180^{\circ}$,射线OC与射线OA重合,并绕点O以每秒$6^{\circ}$的速度逆时针旋转;射线OD与射线OB重合,并绕点O以每秒$3^{\circ}$的速度顺时针旋转. 射线OC与射线OD同时开始旋转,当射线OC与射线OB重合时,整个运动停止. 设运动的时间为t s.
(1)是否存在某个时刻,使得$∠COD的度数是45^{\circ}$?若存在,求出t的值;若不存在,请说明理由;
(2)当t为何值时,射线OB,OC,OD中恰好有一条射线是其余两条射线中某一条射线的伴随线?

答案:解:(1)运动停止时间:180÷6=30(s),t的取值范围0≤t≤30。
OC旋转角度:6t°,OD旋转角度:3t°。
初始时OC与OA重合,OD与OB重合,∠AOB=180°,则初始∠COD=180°。
OC逆时针旋转,OD顺时针旋转,分两种情况:
①OC与OD相遇前:∠COD=180-6t-3t=45,解得t=15。
②OC与OD相遇后:∠COD=6t+3t-180=45,解得t=25。
t=15和t=25均在0≤t≤30内,存在,t=15或25。
(2)分六种情况:
①OC是OA的伴随线:∠AOC=1/2∠BOC,∠AOC=6t,∠BOC=180-6t,6t=1/2(180-6t),解得t=10。
②OA是OC的伴随线:∠AOC=2∠BOC,6t=2(180-6t),解得t=20。
③OD是OB的伴随线:∠BOD=1/2∠AOD,∠BOD=3t,∠AOD=180-3t,3t=1/2(180-3t),解得t=20。
④OB是OD的伴随线:∠BOD=2∠AOD,3t=2(180-3t),解得t=40(>30,舍去)。
⑤OC是OD的伴随线:∠COD=1/2∠DOB(或∠COD=1/2∠DOC,后者不成立),∠COD=|180-9t|,∠DOB=3t,180-9t=1/2×3t(t≤20)或9t-180=1/2×3t(t>20),解得t=16或t=24。
⑥OD是OC的伴随线:∠COD=2∠COB(或∠COD=2∠DOC,后者不成立),∠COB=180-6t,180-9t=2(180-6t)(t≤20)或9t-180=2(180-6t)(t>20),解得t=12或t=36(>30,舍去)。
综上,t=10、12、16、20、24。
OC旋转角度:6t°,OD旋转角度:3t°。
初始时OC与OA重合,OD与OB重合,∠AOB=180°,则初始∠COD=180°。
OC逆时针旋转,OD顺时针旋转,分两种情况:
①OC与OD相遇前:∠COD=180-6t-3t=45,解得t=15。
②OC与OD相遇后:∠COD=6t+3t-180=45,解得t=25。
t=15和t=25均在0≤t≤30内,存在,t=15或25。
(2)分六种情况:
①OC是OA的伴随线:∠AOC=1/2∠BOC,∠AOC=6t,∠BOC=180-6t,6t=1/2(180-6t),解得t=10。
②OA是OC的伴随线:∠AOC=2∠BOC,6t=2(180-6t),解得t=20。
③OD是OB的伴随线:∠BOD=1/2∠AOD,∠BOD=3t,∠AOD=180-3t,3t=1/2(180-3t),解得t=20。
④OB是OD的伴随线:∠BOD=2∠AOD,3t=2(180-3t),解得t=40(>30,舍去)。
⑤OC是OD的伴随线:∠COD=1/2∠DOB(或∠COD=1/2∠DOC,后者不成立),∠COD=|180-9t|,∠DOB=3t,180-9t=1/2×3t(t≤20)或9t-180=1/2×3t(t>20),解得t=16或t=24。
⑥OD是OC的伴随线:∠COD=2∠COB(或∠COD=2∠DOC,后者不成立),∠COB=180-6t,180-9t=2(180-6t)(t≤20)或9t-180=2(180-6t)(t>20),解得t=12或t=36(>30,舍去)。
综上,t=10、12、16、20、24。