二维码的制作
|问题背景|某校组织学科竞赛,学校编程社团为每位考生的准考证号设计二维码.二维码的图案由一系列黑白相间的方块(黑色代表1,白色代表0)组成,形成一串二进制序列,用于存储各种类型的数据.|
|查阅资料一|十进制,即“逢十进一”,使用0~9这十个数字记数,基数为10(基数10常省略不写).例如,十进制数3925表示3个千、9个百、2个十、5个一的和,可得式子:3925= $3×10^{3}+9×10^{2}+2×10^{1}+5×10^{0}$(规定:当$a\neq0$时,$a^{0}= 1$).二进制,即“逢二进一”,各数位上的数字只有0和1,基数为2.例如,二进制数$(10100)_{2}$(角标2为基数,除十进制外,基数不能省略),可利用上述方法将其转化为十进制数:$(10100)_{2}= 1×2^{4}+0×2^{3}+1×2^{2}+0×2^{1}+0×2^{0}= 20$.|
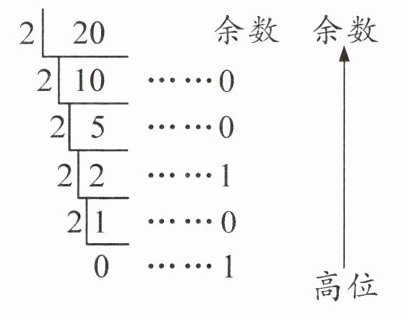
|查阅资料二|根据二进制数“逢二进一”的原则,可以用2连续去除十进制数,直到商0为止,然后逆序取余数,得到二进制数.例如:可得$20= (10100)_{2}$.上述方法可以推广为把十进制数转换为k进制的算法(除k取余法).|
|制作二维码|考生准考证号0207181124的二维码图形和制作说明如图①所示.|

图②是未完成的小张同学准考证号的二维码,完成下列问题:
【图形感知】
(1)根据图①的制作示意图,把小张同学的考场号二进制数$(10101)_{2}$在图②中填涂出来;
【转化计算】
(2)根据如图②所示的二维码图形,求小张同学所在的年级和班级;
【实践操作】
(3)已知小张的准考证座位号是13号,请先转化计算,再完善二维码制作.
|问题背景|某校组织学科竞赛,学校编程社团为每位考生的准考证号设计二维码.二维码的图案由一系列黑白相间的方块(黑色代表1,白色代表0)组成,形成一串二进制序列,用于存储各种类型的数据.|
|查阅资料一|十进制,即“逢十进一”,使用0~9这十个数字记数,基数为10(基数10常省略不写).例如,十进制数3925表示3个千、9个百、2个十、5个一的和,可得式子:3925= $3×10^{3}+9×10^{2}+2×10^{1}+5×10^{0}$(规定:当$a\neq0$时,$a^{0}= 1$).二进制,即“逢二进一”,各数位上的数字只有0和1,基数为2.例如,二进制数$(10100)_{2}$(角标2为基数,除十进制外,基数不能省略),可利用上述方法将其转化为十进制数:$(10100)_{2}= 1×2^{4}+0×2^{3}+1×2^{2}+0×2^{1}+0×2^{0}= 20$.|
|查阅资料二|根据二进制数“逢二进一”的原则,可以用2连续去除十进制数,直到商0为止,然后逆序取余数,得到二进制数.例如:可得$20= (10100)_{2}$.上述方法可以推广为把十进制数转换为k进制的算法(除k取余法).|

|制作二维码|考生准考证号0207181124的二维码图形和制作说明如图①所示.|

图②是未完成的小张同学准考证号的二维码,完成下列问题:
【图形感知】
(1)根据图①的制作示意图,把小张同学的考场号二进制数$(10101)_{2}$在图②中填涂出来;
【转化计算】
(2)根据如图②所示的二维码图形,求小张同学所在的年级和班级;
【实践操作】
(3)已知小张的准考证座位号是13号,请先转化计算,再完善二维码制作.
答案:【解析】:
(1)二进制数$(10101)_2$转化为十进制数为:
$1 × 2^4 + 0 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 16 + 0 + 4 + 0 + 1 = 21$,
根据图①的制作示意图,黑色代表1,白色代表0,
所以,在图②中,从右往左数,第5个格子涂黑(代表$2^4$),第3个格子涂黑(代表$2^2$),第1个格子涂黑(代表$2^0$),其余格子保持白色。
(2)从图②中,可以得到小张同学准考证号的二进制数为:
年级:$(111)_2$,
班级:$(10010)_2$,
转化为十进制数:
年级:$1 × 2^2 + 1 × 2^1 + 1 × 2^0 = 4 + 2 + 1 = 7$,
班级:$1 × 2^4 + 0 × 2^3 + 0 × 2^2 + 1 × 2^1 + 0 × 2^0 = 16 + 0 + 0 + 2 + 0 = 18$,
所以,小张同学所在的年级是7年级,班级是18班。
(3)小张的准考证座位号是13号,转化为二进制数:
$13 ÷ 2 = 6 \ldots 1$,
$6 ÷ 2 = 3 \ldots 0$,
$3 ÷ 2 = 1 \ldots 1$,
$1 ÷ 2 = 0 \ldots 1$,
所以,$13 = (1101)_2$,
根据二进制数$(1101)_2$,在图②中,从右往左数,第4个格子涂黑(代表$2^3$),第3个格子涂黑(代表$2^2$),第1个格子涂黑(代表$2^0$),其余格子保持原样或涂为白色。
【答案】:
(1)在图②中,从右往左数,第5个、第3个和第1个格子涂黑,其余格子保持白色。
(2)小张同学所在的年级是7年级,班级是18班。
(3)小张的准考证座位号的二进制数为$(1101)_2$,在图②中,从右往左数,第4个、第3个和第1个格子涂黑,其余格子保持原样或涂为白色。
(1)二进制数$(10101)_2$转化为十进制数为:
$1 × 2^4 + 0 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 16 + 0 + 4 + 0 + 1 = 21$,
根据图①的制作示意图,黑色代表1,白色代表0,
所以,在图②中,从右往左数,第5个格子涂黑(代表$2^4$),第3个格子涂黑(代表$2^2$),第1个格子涂黑(代表$2^0$),其余格子保持白色。
(2)从图②中,可以得到小张同学准考证号的二进制数为:
年级:$(111)_2$,
班级:$(10010)_2$,
转化为十进制数:
年级:$1 × 2^2 + 1 × 2^1 + 1 × 2^0 = 4 + 2 + 1 = 7$,
班级:$1 × 2^4 + 0 × 2^3 + 0 × 2^2 + 1 × 2^1 + 0 × 2^0 = 16 + 0 + 0 + 2 + 0 = 18$,
所以,小张同学所在的年级是7年级,班级是18班。
(3)小张的准考证座位号是13号,转化为二进制数:
$13 ÷ 2 = 6 \ldots 1$,
$6 ÷ 2 = 3 \ldots 0$,
$3 ÷ 2 = 1 \ldots 1$,
$1 ÷ 2 = 0 \ldots 1$,
所以,$13 = (1101)_2$,
根据二进制数$(1101)_2$,在图②中,从右往左数,第4个格子涂黑(代表$2^3$),第3个格子涂黑(代表$2^2$),第1个格子涂黑(代表$2^0$),其余格子保持原样或涂为白色。
【答案】:
(1)在图②中,从右往左数,第5个、第3个和第1个格子涂黑,其余格子保持白色。
(2)小张同学所在的年级是7年级,班级是18班。
(3)小张的准考证座位号的二进制数为$(1101)_2$,在图②中,从右往左数,第4个、第3个和第1个格子涂黑,其余格子保持原样或涂为白色。