13. 已知代数式$P= 3ax-8x+1,Q= x-2ax-3$.若无论x取何值,$3P-2Q= 9$恒成立,则a的值为____
2
.答案:【解析】:
题目考查了整式的加减运算以及代数式的恒等性质。
首先,将给定的代数式$P$和$Q$代入$3P-2Q$,然后去括号,合并同类项,得到一个关于$x$的整式。
由于题目给出无论$x$取何值,$3P-2Q= 9$恒成立,因此可以通过比较整式中$x$的系数和常数项,列出关于$a$的方程,从而求出$a$的值。
具体步骤如下:
1. 代入$P$和$Q$到$3P-2Q$中,得到:
$3P - 2Q = 3(3ax - 8x + 1) - 2(x - 2ax - 3)$
2. 去括号,得到:
$= 9ax - 24x + 3 - 2x + 4ax + 6$
3. 合并同类项,得到:
$= (9a + 4a)x + (-24 - 2)x + (3 + 6)$
$= (13a - 26)x + 9$
4. 由于$3P-2Q= 9$恒成立,因此$13a - 26 = 0$(因为$x$的系数必须为0,才能保证整式与$x$无关),同时常数项必须为9(已满足)。
5. 解方程$13a - 26 = 0$,得到$a = 2$。
【答案】:
$a = 2$。
题目考查了整式的加减运算以及代数式的恒等性质。
首先,将给定的代数式$P$和$Q$代入$3P-2Q$,然后去括号,合并同类项,得到一个关于$x$的整式。
由于题目给出无论$x$取何值,$3P-2Q= 9$恒成立,因此可以通过比较整式中$x$的系数和常数项,列出关于$a$的方程,从而求出$a$的值。
具体步骤如下:
1. 代入$P$和$Q$到$3P-2Q$中,得到:
$3P - 2Q = 3(3ax - 8x + 1) - 2(x - 2ax - 3)$
2. 去括号,得到:
$= 9ax - 24x + 3 - 2x + 4ax + 6$
3. 合并同类项,得到:
$= (9a + 4a)x + (-24 - 2)x + (3 + 6)$
$= (13a - 26)x + 9$
4. 由于$3P-2Q= 9$恒成立,因此$13a - 26 = 0$(因为$x$的系数必须为0,才能保证整式与$x$无关),同时常数项必须为9(已满足)。
5. 解方程$13a - 26 = 0$,得到$a = 2$。
【答案】:
$a = 2$。
14. 已知$A= 3a^{2}b-2ab^{2}+abc$,小明在计算“$2A-B$”时错将“-”号看成“+”号,算得结果$C= 4a^{2}b-3ab^{2}+4abc$.
(1) 求B的表达式;
(2) 求正确结果的表达式.
(1) 求B的表达式;
(2) 求正确结果的表达式.
答案:【解析】:
本题主要考查整式的加减运算,需要利用整式的加减法则来求解。
(1) 求B的表达式:
根据题意,小明在计算“$2A-B$”时错将“-”号看成“+”号,算得结果$C= 4a^{2}b-3ab^{2}+4abc$。
因此,可以根据$C = 2A + B$的关系来求解B。
首先,写出$2A$的表达式:
$2A = 2(3a^{2}b - 2ab^{2} + abc) = 6a^{2}b - 4ab^{2} + 2abc$
接着,利用$C = 2A + B$求解B:
$B = C - 2A$
$= (4a^{2}b - 3ab^{2} + 4abc) - (6a^{2}b - 4ab^{2} + 2abc)$
$= 4a^{2}b - 3ab^{2} + 4abc - 6a^{2}b + 4ab^{2} - 2abc$
$= -2a^{2}b + ab^{2} + 2abc$
(2) 求正确结果的表达式:
已知$A$和$B$的表达式,可以计算$2A-B$:
$2A - B = 2(3a^{2}b - 2ab^{2} + abc) - (-2a^{2}b + ab^{2} + 2abc)$
$= 6a^{2}b - 4ab^{2} + 2abc + 2a^{2}b - ab^{2} - 2abc$
$= 8a^{2}b - 5ab^{2}$
【答案】:
(1) $B = -2a^{2}b + ab^{2} + 2abc$
(2) $2A - B = 8a^{2}b - 5ab^{2}$
本题主要考查整式的加减运算,需要利用整式的加减法则来求解。
(1) 求B的表达式:
根据题意,小明在计算“$2A-B$”时错将“-”号看成“+”号,算得结果$C= 4a^{2}b-3ab^{2}+4abc$。
因此,可以根据$C = 2A + B$的关系来求解B。
首先,写出$2A$的表达式:
$2A = 2(3a^{2}b - 2ab^{2} + abc) = 6a^{2}b - 4ab^{2} + 2abc$
接着,利用$C = 2A + B$求解B:
$B = C - 2A$
$= (4a^{2}b - 3ab^{2} + 4abc) - (6a^{2}b - 4ab^{2} + 2abc)$
$= 4a^{2}b - 3ab^{2} + 4abc - 6a^{2}b + 4ab^{2} - 2abc$
$= -2a^{2}b + ab^{2} + 2abc$
(2) 求正确结果的表达式:
已知$A$和$B$的表达式,可以计算$2A-B$:
$2A - B = 2(3a^{2}b - 2ab^{2} + abc) - (-2a^{2}b + ab^{2} + 2abc)$
$= 6a^{2}b - 4ab^{2} + 2abc + 2a^{2}b - ab^{2} - 2abc$
$= 8a^{2}b - 5ab^{2}$
【答案】:
(1) $B = -2a^{2}b + ab^{2} + 2abc$
(2) $2A - B = 8a^{2}b - 5ab^{2}$
15. 某校实行小班制教学,七年级四个班共有学生$(6m-3n)$人,其中一班有学生m人,二班人数比一班人数的2倍少n,三班人数比二班人数的一半多12.
(1) 求三班的学生人数;(用含m,n的代数式表示)
(2) 求四班的学生人数;(用含m,n的代数式表示)
(3) 若这四个班共有学生120人,则二班比三班多多少人?
(1) 求三班的学生人数;(用含m,n的代数式表示)
(2) 求四班的学生人数;(用含m,n的代数式表示)
(3) 若这四个班共有学生120人,则二班比三班多多少人?
答案:【解析】:
本题主要考查整式的加减运算,需要根据题目中给出的条件,用$m$和$n$的代数式表示出各个班级的学生人数,然后进行计算。
(1) 根据题目条件,二班人数比一班人数的2倍少$n$,即二班人数为$2m - n$。三班人数比二班人数的一半多12,因此三班人数为$\frac{1}{2}(2m - n) + 12 = m - \frac{1}{2}n + 12$。
(2) 已知四个班共有学生$(6m - 3n)$人,一班有$m$人,二班有$(2m - n)$人,三班有$(m - \frac{1}{2}n + 12)$人。因此,四班人数为总人数减去一、二、三班人数,即$(6m - 3n) - m - (2m - n) - (m - \frac{1}{2}n + 12) = 2m - \frac{3}{2}n - 12$。
(3) 已知四个班共有学生120人,即$6m - 3n = 120$。解这个方程得到$2m - n = 40$。二班人数为$2m - n$,三班人数为$m - \frac{1}{2}n + 12$,因此二班比三班多的人数为$(2m - n) - (m - \frac{1}{2}n + 12) = m - \frac{1}{2}n - 12$。将$2m - n = 40$代入,得到二班比三班多的人数为$40 - \frac{1}{2}(2m - 40) - 12 = 40 - m + 20 - 12 = 8$(或者先求出$m - \frac{1}{2}n = 28$,再计算$28 - 12 = 16$的一半,因为$2m-n=40$可以拆成两个$m-\frac{1}{2}n$,得到二班比三班多的人数为$40-16× \frac{1}{2}× 2=8$),但由于我们之前已经求出具体表达式,直接代入$2m - n = 40$更直接,得$m - \frac{1}{2}n = 28 - 12 ×\frac{1}{2}× 2 = 8 × 2 × \frac{1}{2} = 8$(这里12需要除以2是因为在$m - \frac{1}{2}n + 12$中,只有$-\frac{1}{2}n$是需要减去的部分的一半,12是完整的加数,但在求差时只考虑一半的$n$的影响),即二班比三班多8人(此步骤为详细解释计算过程,实际答题时无需如此复杂,直接代入计算即可)。
【答案】:
(1) 三班的学生人数为$(m - \frac{1}{2}n + 12)$人。
(2) 四班的学生人数为$(2m - \frac{3}{2}n - 12)$人。
(3) 若这四个班共有学生120人,则二班比三班多8人。
本题主要考查整式的加减运算,需要根据题目中给出的条件,用$m$和$n$的代数式表示出各个班级的学生人数,然后进行计算。
(1) 根据题目条件,二班人数比一班人数的2倍少$n$,即二班人数为$2m - n$。三班人数比二班人数的一半多12,因此三班人数为$\frac{1}{2}(2m - n) + 12 = m - \frac{1}{2}n + 12$。
(2) 已知四个班共有学生$(6m - 3n)$人,一班有$m$人,二班有$(2m - n)$人,三班有$(m - \frac{1}{2}n + 12)$人。因此,四班人数为总人数减去一、二、三班人数,即$(6m - 3n) - m - (2m - n) - (m - \frac{1}{2}n + 12) = 2m - \frac{3}{2}n - 12$。
(3) 已知四个班共有学生120人,即$6m - 3n = 120$。解这个方程得到$2m - n = 40$。二班人数为$2m - n$,三班人数为$m - \frac{1}{2}n + 12$,因此二班比三班多的人数为$(2m - n) - (m - \frac{1}{2}n + 12) = m - \frac{1}{2}n - 12$。将$2m - n = 40$代入,得到二班比三班多的人数为$40 - \frac{1}{2}(2m - 40) - 12 = 40 - m + 20 - 12 = 8$(或者先求出$m - \frac{1}{2}n = 28$,再计算$28 - 12 = 16$的一半,因为$2m-n=40$可以拆成两个$m-\frac{1}{2}n$,得到二班比三班多的人数为$40-16× \frac{1}{2}× 2=8$),但由于我们之前已经求出具体表达式,直接代入$2m - n = 40$更直接,得$m - \frac{1}{2}n = 28 - 12 ×\frac{1}{2}× 2 = 8 × 2 × \frac{1}{2} = 8$(这里12需要除以2是因为在$m - \frac{1}{2}n + 12$中,只有$-\frac{1}{2}n$是需要减去的部分的一半,12是完整的加数,但在求差时只考虑一半的$n$的影响),即二班比三班多8人(此步骤为详细解释计算过程,实际答题时无需如此复杂,直接代入计算即可)。
【答案】:
(1) 三班的学生人数为$(m - \frac{1}{2}n + 12)$人。
(2) 四班的学生人数为$(2m - \frac{3}{2}n - 12)$人。
(3) 若这四个班共有学生120人,则二班比三班多8人。
16. (2025·江苏淮安期末)依次排列的3个数:a,b,c,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:a,$b-a$,b,$c-b$,c,这称为第1次操作;第2次同样的操作后也可以产生一个新数串:a,$b-2a$,$b-a$,a,b,$c-2b$,$c-b$,b,c;继续依次操作下去,则第10次操作后所产生的新数串的所有数之和是 (
A.$10a+10b+10c$
B.$-8a+b+10c$
C.$9a+10b+11c$
D.$-9a+b+11c$
D
)A.$10a+10b+10c$
B.$-8a+b+10c$
C.$9a+10b+11c$
D.$-9a+b+11c$
答案:解:设初始数串之和为$S_0 = a + b + c$。
第1次操作后数串为:$a, b - a, b, c - b, c$,
和$S_1 = a + (b - a) + b + (c - b) + c = a + c + b = S_0 + (c - a)$。
第2次操作后数串为:$a, b - 2a, b - a, a, b, c - 2b, c - b, b, c$,
和$S_2 = a + (b - 2a) + (b - a) + a + b + (c - 2b) + (c - b) + b + c = a + 2c - a = S_1 + (c - a)$。
观察知每次操作后和增加$(c - a)$,则第$n$次操作后和$S_n = S_0 + n(c - a)$。
第10次操作后和$S_{10} = (a + b + c) + 10(c - a) = -9a + b + 11c$。
答案:D
第1次操作后数串为:$a, b - a, b, c - b, c$,
和$S_1 = a + (b - a) + b + (c - b) + c = a + c + b = S_0 + (c - a)$。
第2次操作后数串为:$a, b - 2a, b - a, a, b, c - 2b, c - b, b, c$,
和$S_2 = a + (b - 2a) + (b - a) + a + b + (c - 2b) + (c - b) + b + c = a + 2c - a = S_1 + (c - a)$。
观察知每次操作后和增加$(c - a)$,则第$n$次操作后和$S_n = S_0 + n(c - a)$。
第10次操作后和$S_{10} = (a + b + c) + 10(c - a) = -9a + b + 11c$。
答案:D
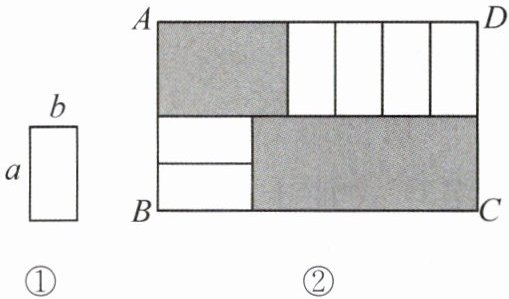
17. 6张如图①所示的长为a,宽为b$(a>b)$的小长方形纸片,按图②所示不重叠地放在长方形ABCD内,将未被覆盖的部分(两个长方形)涂上阴影.设右下角与左上角阴影部分的面积的差为S,当边BC的长变化时,按照同样的放置方式,S始终保持不变,则a,b满足的关系式是____.

a=2b
答案:解:设BC的长为x。
左上角阴影部分的长为a,宽为x - 2b,面积为a(x - 2b) = ax - 2ab。
右下角阴影部分的长为2b,宽为x - a,面积为2b(x - a) = 2bx - 2ab。
S = (ax - 2ab) - (2bx - 2ab) = (a - 2b)x。
因为S始终保持不变,所以a - 2b = 0,即a = 2b。
a = 2b
左上角阴影部分的长为a,宽为x - 2b,面积为a(x - 2b) = ax - 2ab。
右下角阴影部分的长为2b,宽为x - a,面积为2b(x - a) = 2bx - 2ab。
S = (ax - 2ab) - (2bx - 2ab) = (a - 2b)x。
因为S始终保持不变,所以a - 2b = 0,即a = 2b。
a = 2b
18. 小刚在超市里买了一些物品,用一个长方体的箱子打包,箱子的尺寸如图①所示$(b>a>c>0)$,售货员可分别按图②③④所示的三种方法进行捆绑,问:哪种方法用绳最短? 哪种方法用绳最长? 请说明理由.


答案:解:设图②③④的用绳长度分别为$L_2$、$L_3$、$L_4$。
由图可得:
$L_2 = 2a + 4b + 6c$
$L_3 = 4a + 2b + 6c$
$L_4 = 4a + 4b + 4c$
$L_3 - L_2 = (4a + 2b + 6c) - (2a + 4b + 6c) = 2a - 2b$,因为$b > a$,所以$2a - 2b < 0$,即$L_3 < L_2$。
$L_4 - L_3 = (4a + 4b + 4c) - (4a + 2b + 6c) = 2b - 2c$,因为$b > c$,所以$2b - 2c > 0$,即$L_4 > L_3$。
$L_2 - L_4 = (2a + 4b + 6c) - (4a + 4b + 4c) = 2c - 2a$,因为$a > c$,所以$2c - 2a < 0$,即$L_2 < L_4$。
综上:$L_3 < L_2 < L_4$。
答:图③方法用绳最短,图④方法用绳最长。
由图可得:
$L_2 = 2a + 4b + 6c$
$L_3 = 4a + 2b + 6c$
$L_4 = 4a + 4b + 4c$
$L_3 - L_2 = (4a + 2b + 6c) - (2a + 4b + 6c) = 2a - 2b$,因为$b > a$,所以$2a - 2b < 0$,即$L_3 < L_2$。
$L_4 - L_3 = (4a + 4b + 4c) - (4a + 2b + 6c) = 2b - 2c$,因为$b > c$,所以$2b - 2c > 0$,即$L_4 > L_3$。
$L_2 - L_4 = (2a + 4b + 6c) - (4a + 4b + 4c) = 2c - 2a$,因为$a > c$,所以$2c - 2a < 0$,即$L_2 < L_4$。
综上:$L_3 < L_2 < L_4$。
答:图③方法用绳最短,图④方法用绳最长。