1. 为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动. 现需购买甲、乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本. 设购买甲种读本x本,则购买乙种读本的费用为(
A.8x元
B.10(100 - x)元
C.8(100 - x)元
D.(100 - 8x)元
C
)A.8x元
B.10(100 - x)元
C.8(100 - x)元
D.(100 - 8x)元
答案:【解析】:
本题主要考查的是列代数式。
首先,根据题目描述,甲种读本的单价是10元/本,购买数量为$x$本,所以甲种读本的总费用是$10x$元。
乙种读本的单价是8元/本,由于甲、乙两种读本共100本,所以乙种读本的购买数量是$(100 - x)$本。
因此,乙种读本的总费用是$8 × (100 - x)$元,即$8(100 - x)$元。
接下来,我们需要从选项中找出与这个表达式相匹配的答案。
A选项:$8x$元,这表示的是如果全部购买甲种读本且数量为$x$时的费用(但单价不对),或者如果全部购买乙种读本且数量为$x$时的费用(但数量不对),所以A选项错误。
B选项:$10(100 - x)$元,这表示的是如果全部购买甲种读本且数量为$(100 - x)$时的费用(但单价和数量都不对),所以B选项错误。
C选项:$8(100 - x)$元,这与我们之前计算出的乙种读本的总费用表达式一致,所以C选项正确。
D选项:$(100 - 8x)$元,这个表达式没有正确的物理意义(它不代表任何读本的总费用),所以D选项错误。
综上所述,购买乙种读本的费用为$8(100 - x)$元,故选C。
【答案】:
C
本题主要考查的是列代数式。
首先,根据题目描述,甲种读本的单价是10元/本,购买数量为$x$本,所以甲种读本的总费用是$10x$元。
乙种读本的单价是8元/本,由于甲、乙两种读本共100本,所以乙种读本的购买数量是$(100 - x)$本。
因此,乙种读本的总费用是$8 × (100 - x)$元,即$8(100 - x)$元。
接下来,我们需要从选项中找出与这个表达式相匹配的答案。
A选项:$8x$元,这表示的是如果全部购买甲种读本且数量为$x$时的费用(但单价不对),或者如果全部购买乙种读本且数量为$x$时的费用(但数量不对),所以A选项错误。
B选项:$10(100 - x)$元,这表示的是如果全部购买甲种读本且数量为$(100 - x)$时的费用(但单价和数量都不对),所以B选项错误。
C选项:$8(100 - x)$元,这与我们之前计算出的乙种读本的总费用表达式一致,所以C选项正确。
D选项:$(100 - 8x)$元,这个表达式没有正确的物理意义(它不代表任何读本的总费用),所以D选项错误。
综上所述,购买乙种读本的费用为$8(100 - x)$元,故选C。
【答案】:
C
2. 某商品的进价为m元/件,在进价基础上加价25%后优惠10%出售,则该商品的售价为
$\frac{9}{8}m$(或 $1.125m$)
元/件.答案:【解析】:
本题主要考查百分数运算和代数表达式的建立。
首先,商品在进价基础上加价$25\%$,加价后的价格就是进价的$125\%$,即$1.25m$元/件。
然后,这个加价后的商品再优惠$10\%$,即售价是加价后价格的$90\%$。
因此,可以通过建立代数表达式来找出商品的售价。
具体步骤如下:
1. 计算加价后的价格:在进价$m$元/件的基础上加价$25\%$,即 $m × 1.25 = 1.25m$(元/件)。
2. 计算优惠后的价格:加价后的价格打$9$折,即 $1.25m × 0.9$。
将这个表达式化简,得到商品的售价为 $1.125m$ 元/件,也可以表示为 $\frac{9}{8}m$ 元/件。
【答案】:
$\frac{9}{8}m$(或 $1.125m$)
本题主要考查百分数运算和代数表达式的建立。
首先,商品在进价基础上加价$25\%$,加价后的价格就是进价的$125\%$,即$1.25m$元/件。
然后,这个加价后的商品再优惠$10\%$,即售价是加价后价格的$90\%$。
因此,可以通过建立代数表达式来找出商品的售价。
具体步骤如下:
1. 计算加价后的价格:在进价$m$元/件的基础上加价$25\%$,即 $m × 1.25 = 1.25m$(元/件)。
2. 计算优惠后的价格:加价后的价格打$9$折,即 $1.25m × 0.9$。
将这个表达式化简,得到商品的售价为 $1.125m$ 元/件,也可以表示为 $\frac{9}{8}m$ 元/件。
【答案】:
$\frac{9}{8}m$(或 $1.125m$)
3. 若多项式$x^{a}y - x^{2} + by^{3}$是三次二项式,则a =
2
,b = 0
.答案:【解析】:
首先,我们分析多项式的次数。多项式的次数是由它的各项中次数最高的那一项决定的。
对于多项式$x^{a}y - x^{2} + by^{3}$,我们需要确定哪一项是三次项。
1. 考虑第一项$x^{a}y$,它的次数是$a+1$(因为x的次数是a,y的次数是1)。
2. 考虑第二项$-x^{2}$,它是二次项,所以不是我们要找的三项式中的三次项。
3. 考虑第三项$by^{3}$,它是三次项,但由于b是系数,我们可以通过设置b=0来消除这一项,使其不影响多项式的次数。
为了使多项式成为三次二项式,我们需要:
1. $a+1=3$,从而得到$a=2$。
2. $b=0$,这样$by^{3}$这一项就消失了,确保多项式是二项式。
【答案】:
$a = 2$;$b = 0$。
首先,我们分析多项式的次数。多项式的次数是由它的各项中次数最高的那一项决定的。
对于多项式$x^{a}y - x^{2} + by^{3}$,我们需要确定哪一项是三次项。
1. 考虑第一项$x^{a}y$,它的次数是$a+1$(因为x的次数是a,y的次数是1)。
2. 考虑第二项$-x^{2}$,它是二次项,所以不是我们要找的三项式中的三次项。
3. 考虑第三项$by^{3}$,它是三次项,但由于b是系数,我们可以通过设置b=0来消除这一项,使其不影响多项式的次数。
为了使多项式成为三次二项式,我们需要:
1. $a+1=3$,从而得到$a=2$。
2. $b=0$,这样$by^{3}$这一项就消失了,确保多项式是二项式。
【答案】:
$a = 2$;$b = 0$。
4. (2025·江苏连云港期末)如图所示的运算程序中,若输入的x的值分别是30,91,则输出的结果分别是(
A.33,94
B.15,94
C.15,47
D.33,47
B
)A.33,94
B.15,94
C.15,47
D.33,47
答案:【解析】:
本题可根据所给的运算程序,分别将$x = 30$和$x = 91$代入程序进行计算,从而得出输出的结果。
运算程序为:当输入$x$时,判断$x$是奇数还是偶数,若$x$是偶数,则输出$\frac{1}{2}x$;若$x$是奇数,则输出$x + 3$。
当$x = 30$时,因为$30$是偶数,根据运算程序,应执行$\frac{1}{2}x$这一运算,将$x = 30$代入$\frac{1}{2}x$可得:$\frac{1}{2}×30 = 15$。
当$x = 91$时,因为$91$是奇数,根据运算程序,应执行$x + 3$这一运算,将$x = 91$代入$x + 3$可得:$91 + 3 = 94$。
所以,当输入的$x$的值分别是$30$,$91$时,输出的结果分别是$15$,$94$。
【答案】:B
本题可根据所给的运算程序,分别将$x = 30$和$x = 91$代入程序进行计算,从而得出输出的结果。
运算程序为:当输入$x$时,判断$x$是奇数还是偶数,若$x$是偶数,则输出$\frac{1}{2}x$;若$x$是奇数,则输出$x + 3$。
当$x = 30$时,因为$30$是偶数,根据运算程序,应执行$\frac{1}{2}x$这一运算,将$x = 30$代入$\frac{1}{2}x$可得:$\frac{1}{2}×30 = 15$。
当$x = 91$时,因为$91$是奇数,根据运算程序,应执行$x + 3$这一运算,将$x = 91$代入$x + 3$可得:$91 + 3 = 94$。
所以,当输入的$x$的值分别是$30$,$91$时,输出的结果分别是$15$,$94$。
【答案】:B
5. (2024·广东广州)若$a^{2} - 2a - 5 = 0$,则$2a^{2} - 4a + 1 = $
11
.答案:【解析】:
本题主要考察代数式的代入法求解。
首先,我们有给定的方程 $a^{2} - 2a - 5 = 0$。
我们需要求 $2a^{2} - 4a + 1$ 的值。
观察目标表达式 $2a^{2} - 4a + 1$,我们可以发现它可以写成 $2(a^{2} - 2a) + 1$ 的形式。
根据给定方程 $a^{2} - 2a - 5 = 0$,我们可以得到 $a^{2} - 2a = 5$。
代入得:
$2a^{2} - 4a + 1 = 2(a^{2} - 2a) + 1 = 2 × 5 + 1 = 10 + 1 = 11$
【答案】:
$11$
本题主要考察代数式的代入法求解。
首先,我们有给定的方程 $a^{2} - 2a - 5 = 0$。
我们需要求 $2a^{2} - 4a + 1$ 的值。
观察目标表达式 $2a^{2} - 4a + 1$,我们可以发现它可以写成 $2(a^{2} - 2a) + 1$ 的形式。
根据给定方程 $a^{2} - 2a - 5 = 0$,我们可以得到 $a^{2} - 2a = 5$。
代入得:
$2a^{2} - 4a + 1 = 2(a^{2} - 2a) + 1 = 2 × 5 + 1 = 10 + 1 = 11$
【答案】:
$11$
6. 如图是一个运算程序的示意图. 若开始输入的x的值为27,则第2025次输出的结果为
1
.答案:解:第1次:输入27,$27\neq1$,输出$\frac{1}{3}×27 = 9$;
第2次:输入9,$9\neq1$,输出$\frac{1}{3}×9 = 3$;
第3次:输入3,$3\neq1$,输出$\frac{1}{3}×3 = 1$;
第4次:输入1,$1 = 1$,输出$1 + 2 = 3$;
第5次:输入3,$3\neq1$,输出$\frac{1}{3}×3 = 1$;
第6次:输入1,$1 = 1$,输出$1 + 2 = 3$;
……
从第2次开始,输出结果以3,1循环,循环节长度为2。
$(2025 - 1)÷2=1012$,余数为0,故第2025次输出的结果为1。
1
第2次:输入9,$9\neq1$,输出$\frac{1}{3}×9 = 3$;
第3次:输入3,$3\neq1$,输出$\frac{1}{3}×3 = 1$;
第4次:输入1,$1 = 1$,输出$1 + 2 = 3$;
第5次:输入3,$3\neq1$,输出$\frac{1}{3}×3 = 1$;
第6次:输入1,$1 = 1$,输出$1 + 2 = 3$;
……
从第2次开始,输出结果以3,1循环,循环节长度为2。
$(2025 - 1)÷2=1012$,余数为0,故第2025次输出的结果为1。
1
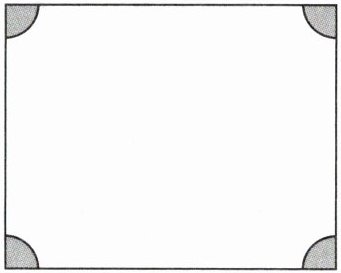
7. 新趋势情境素材如图,某长方形广场的四角都有一块四分之一圆形草地(其余为空地),且圆形草地的半径都为r m,长方形的长为a m,宽为b m.
(1) 用代数式表示这个广场上空地的面积;
(2) 若长方形广场的长为250 m,宽为200 m,圆形草地的半径为25 m,求这个广场上空地的面积.
]
(1) 用代数式表示这个广场上空地的面积;
(2) 若长方形广场的长为250 m,宽为200 m,圆形草地的半径为25 m,求这个广场上空地的面积.
]

答案:【解析】:
(1) 需要求出空地的面积,需要用到长方形的面积公式和圆的面积公式。
长方形的面积公式为:$S_{\text{长方形}} = \text{长} × \text{宽}$。
圆的面积公式为:$S_{\text{圆}} = \pi r^2$。
由于四个角各有一个四分之一的圆,所以四个四分之一的圆合起来就是一个完整的圆。
因此,空地的面积就是长方形的面积减去一个圆的面积。
(2) 需要将给定的数值代入到第一问求出的代数式中,计算出空地的具体面积。
【答案】:
(1) 解:长方形的面积是 $ab$ 平方米。
一个四分之一圆的面积是 $\frac{1}{4} \pi r^2$ 平方米,
所以四个四分之一圆的面积是 $\pi r^2$ 平方米。
因此,空地的面积为:
$S = ab - \pi r^2$(平方米)。
答:空地的面积为 $(ab - \pi r^2)$ 平方米。
(2) 解:当 $a = 250$,$b = 200$,$r = 25$ 时,
代入 $S = ab - \pi r^2$,
$S = 250 × 200 - \pi × 25^2$
$= 50000 - 625\pi$(平方米)
$\approx 50000 - 625 × 3.14$
$= 50000 - 1962.5$
$= 48037.5$(平方米)
答:空地的面积为 48037.5 平方米。
(1) 需要求出空地的面积,需要用到长方形的面积公式和圆的面积公式。
长方形的面积公式为:$S_{\text{长方形}} = \text{长} × \text{宽}$。
圆的面积公式为:$S_{\text{圆}} = \pi r^2$。
由于四个角各有一个四分之一的圆,所以四个四分之一的圆合起来就是一个完整的圆。
因此,空地的面积就是长方形的面积减去一个圆的面积。
(2) 需要将给定的数值代入到第一问求出的代数式中,计算出空地的具体面积。
【答案】:
(1) 解:长方形的面积是 $ab$ 平方米。
一个四分之一圆的面积是 $\frac{1}{4} \pi r^2$ 平方米,
所以四个四分之一圆的面积是 $\pi r^2$ 平方米。
因此,空地的面积为:
$S = ab - \pi r^2$(平方米)。
答:空地的面积为 $(ab - \pi r^2)$ 平方米。
(2) 解:当 $a = 250$,$b = 200$,$r = 25$ 时,
代入 $S = ab - \pi r^2$,
$S = 250 × 200 - \pi × 25^2$
$= 50000 - 625\pi$(平方米)
$\approx 50000 - 625 × 3.14$
$= 50000 - 1962.5$
$= 48037.5$(平方米)
答:空地的面积为 48037.5 平方米。
8. (2024·江苏常州)计算$2a^{2} - a^{2}$的结果是(
A.2
B.$a^{2}$
C.$3a^{2}$
D.$2a^{4}$
B
)A.2
B.$a^{2}$
C.$3a^{2}$
D.$2a^{4}$
答案:【解析】:
本题主要考查了合并同类项的知识点。在代数式中,同类项是指次数、字母均相同的项,它们可以进行合并。本题中的$2a^{2}$和$-a^{2}$就是同类项,根据合并同类项的法则,即系数相加,字母部分保持不变,我们可以将这两项合并为一项。
具体计算过程如下:
$2a^{2} - a^{2} = (2-1)a^{2} = a^{2}$
【答案】:
B
本题主要考查了合并同类项的知识点。在代数式中,同类项是指次数、字母均相同的项,它们可以进行合并。本题中的$2a^{2}$和$-a^{2}$就是同类项,根据合并同类项的法则,即系数相加,字母部分保持不变,我们可以将这两项合并为一项。
具体计算过程如下:
$2a^{2} - a^{2} = (2-1)a^{2} = a^{2}$
【答案】:
B
9. 如果单项式$3x^{m}y与-5x^{3}y^{n}$是同类项,那么m + n =
4
.答案:【解析】:
本题主要考查同类项的定义,即两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项。
根据同类项的定义,我们可以知道,单项式$3x^{m}y$与$-5x^{3}y^{n}$中,$x$的指数应该相等,$y$的指数也应该相等。
因此,我们有$m = 3$,$n = 1$。
接下来,我们需要求出$m + n$的值,即$m + n = 3 + 1 = 4$。
【答案】:
$4$
本题主要考查同类项的定义,即两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项。
根据同类项的定义,我们可以知道,单项式$3x^{m}y$与$-5x^{3}y^{n}$中,$x$的指数应该相等,$y$的指数也应该相等。
因此,我们有$m = 3$,$n = 1$。
接下来,我们需要求出$m + n$的值,即$m + n = 3 + 1 = 4$。
【答案】:
$4$
10. 若单项式$-4x^{m - 2}y^{3}与单项式\frac{2}{3}x^{2}y^{7 - 2n}$的和仍是单项式,求代数式$m^{2} + n^{2} - (2^{m} - 2^{n})$的值.
答案:【解析】:
此题主要考查同类项的概念以及代数式的求值。根据同类项的定义,两个单项式所含字母相同,且相同字母的指数也相同,那么这两个单项式就是同类项。由题意知,单项式$-4x^{m - 2}y^{3}$与单项式$\frac{2}{3}x^{2}y^{7 - 2n}$的和仍是单项式,说明它们是同类项。
根据同类项的性质,我们可以得到两个方程:
$m - 2 = 2$,从中解得$m = 4$;
$7 - 2n = 3$,从中解得$n = 2$。
将$m$和$n$的值代入到代数式$m^{2} + n^{2} - (2^{m} - 2^{n})$中,进行计算。
【答案】:
解:
由于单项式$-4x^{m - 2}y^{3}$与单项式$\frac{2}{3}x^{2}y^{7 - 2n}$的和仍是单项式,根据同类项的定义,我们有:
$m - 2 = 2$,
解得:$m = 4$;
$7 - 2n = 3$,
解得:$n = 2$。
将$m = 4$,$n = 2$代入到代数式$m^{2} + n^{2} - (2^{m} - 2^{n})$中,我们得到:
$m^{2} + n^{2} - (2^{m} - 2^{n})$
$= 4^{2} + 2^{2} - (2^{4} - 2^{2})$
$= 16 + 4 - (16 - 4)$
$= 8$
此题主要考查同类项的概念以及代数式的求值。根据同类项的定义,两个单项式所含字母相同,且相同字母的指数也相同,那么这两个单项式就是同类项。由题意知,单项式$-4x^{m - 2}y^{3}$与单项式$\frac{2}{3}x^{2}y^{7 - 2n}$的和仍是单项式,说明它们是同类项。
根据同类项的性质,我们可以得到两个方程:
$m - 2 = 2$,从中解得$m = 4$;
$7 - 2n = 3$,从中解得$n = 2$。
将$m$和$n$的值代入到代数式$m^{2} + n^{2} - (2^{m} - 2^{n})$中,进行计算。
【答案】:
解:
由于单项式$-4x^{m - 2}y^{3}$与单项式$\frac{2}{3}x^{2}y^{7 - 2n}$的和仍是单项式,根据同类项的定义,我们有:
$m - 2 = 2$,
解得:$m = 4$;
$7 - 2n = 3$,
解得:$n = 2$。
将$m = 4$,$n = 2$代入到代数式$m^{2} + n^{2} - (2^{m} - 2^{n})$中,我们得到:
$m^{2} + n^{2} - (2^{m} - 2^{n})$
$= 4^{2} + 2^{2} - (2^{4} - 2^{2})$
$= 16 + 4 - (16 - 4)$
$= 8$