1. (2023·四川巴中)下面的几何体中,是圆柱的为 (
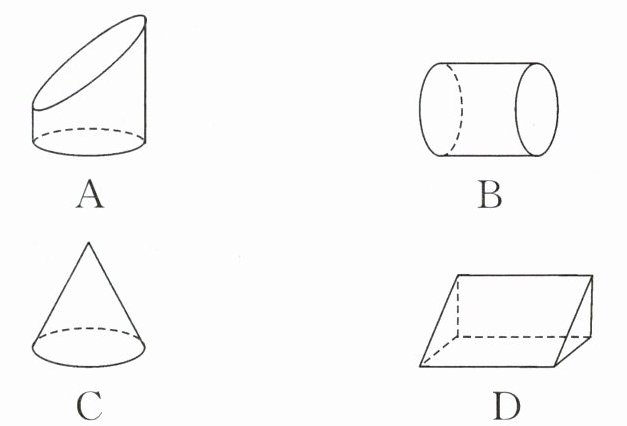
B
)
答案:【解析】:
本题考查圆柱的识别,圆柱的特征是:上、下底面是两个完全相同的圆,侧面是一个曲面,展开后是一个长方形。
选项A:上、下底面不相同,不是圆柱。
选项B:上、下底面是两个完全相同的圆,侧面是一个曲面,符合圆柱的特征,是圆柱。
选项C:只有一个底面是圆,另一个面是顶点,是圆锥,不是圆柱。
选项D:六个面都是长方形,是长方体,不是圆柱。
【答案】:B
本题考查圆柱的识别,圆柱的特征是:上、下底面是两个完全相同的圆,侧面是一个曲面,展开后是一个长方形。
选项A:上、下底面不相同,不是圆柱。
选项B:上、下底面是两个完全相同的圆,侧面是一个曲面,符合圆柱的特征,是圆柱。
选项C:只有一个底面是圆,另一个面是顶点,是圆锥,不是圆柱。
选项D:六个面都是长方形,是长方体,不是圆柱。
【答案】:B
2. 若一个棱柱有 16 个顶点,则这个棱柱有
8
个侧面,有24
条棱.答案:【解析】:
这是一个关于棱柱的问题,棱柱的顶点数、侧面数和棱数之间有一定的关系。
对于一个$n$棱柱,它有$2n$个顶点,$n$个侧面,和$3n$条棱(包括底面和顶面的$2n$条边,以及连接底面和顶面的$n$条侧棱)。
题目给出棱柱有16个顶点,我们可以通过这个信息来找出棱柱的边数$n$。
设棱柱为$n$棱柱,则有$2n = 16$,解得$n = 8$。
所以,这个棱柱是一个八棱柱,有8个侧面和$3 × 8 = 24$条棱。
【答案】:
8;24
这是一个关于棱柱的问题,棱柱的顶点数、侧面数和棱数之间有一定的关系。
对于一个$n$棱柱,它有$2n$个顶点,$n$个侧面,和$3n$条棱(包括底面和顶面的$2n$条边,以及连接底面和顶面的$n$条侧棱)。
题目给出棱柱有16个顶点,我们可以通过这个信息来找出棱柱的边数$n$。
设棱柱为$n$棱柱,则有$2n = 16$,解得$n = 8$。
所以,这个棱柱是一个八棱柱,有8个侧面和$3 × 8 = 24$条棱。
【答案】:
8;24
3. 如图是一组几何体.

(1) 分别写出这些几何体的名称;
(2) 将这些几何体进行适当的分类,并说明分类标准.

(1) 分别写出这些几何体的名称;
(2) 将这些几何体进行适当的分类,并说明分类标准.
答案:(1) ①四棱柱;②圆锥;③球;④圆柱;⑤四棱锥。
(2) 按柱体、锥体、球体分类:柱体:①④;锥体:②⑤;球体:③。(分类标准不唯一,合理即可)
(2) 按柱体、锥体、球体分类:柱体:①④;锥体:②⑤;球体:③。(分类标准不唯一,合理即可)
4. (2025·江苏宿迁期末)对如图所示的变换顺序描述正确的是 (
A.翻折、旋转、平移
B.旋转、翻折、平移
C.平移、翻折、旋转
D.翻折、平移、旋转
D
)A.翻折、旋转、平移
B.旋转、翻折、平移
C.平移、翻折、旋转
D.翻折、平移、旋转
答案:解:观察图形变换过程:
1. 第一个图形到第二个图形,左右眼睛和嘴巴位置互换,符合翻折特征;
2. 第二个图形到第三个图形,形状、方向未变,位置未发生明显平移,保持翻折后的状态;
3. 第三个图形到第四个图形,整体绕某点旋转180°,眼睛和嘴巴位置均旋转至对侧。
变换顺序为翻折、旋转。但选项中无此组合,重新分析:第一个到第二个是翻折,第二个到第三个无变化(可视为平移0距离),第三个到第四个是旋转。
答案:D
1. 第一个图形到第二个图形,左右眼睛和嘴巴位置互换,符合翻折特征;
2. 第二个图形到第三个图形,形状、方向未变,位置未发生明显平移,保持翻折后的状态;
3. 第三个图形到第四个图形,整体绕某点旋转180°,眼睛和嘴巴位置均旋转至对侧。
变换顺序为翻折、旋转。但选项中无此组合,重新分析:第一个到第二个是翻折,第二个到第三个无变化(可视为平移0距离),第三个到第四个是旋转。
答案:D
5. 电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,这说明
线动成面
.答案:【解析】:
这道题目考查的是对几何图形变换的理解,特别是点、线、面、体之间的动态关系。在《西游记》中,孙悟空的“金箍棒”飞速旋转形成一个圆面的描述,实际上是一个线动成面的实例。当金箍棒(代表一条线)在空间中飞速旋转时,它的运动轨迹会形成一个连续的圆面。这符合几何学中“线动成面”的基本原理。
【答案】:
线动成面。
这道题目考查的是对几何图形变换的理解,特别是点、线、面、体之间的动态关系。在《西游记》中,孙悟空的“金箍棒”飞速旋转形成一个圆面的描述,实际上是一个线动成面的实例。当金箍棒(代表一条线)在空间中飞速旋转时,它的运动轨迹会形成一个连续的圆面。这符合几何学中“线动成面”的基本原理。
【答案】:
线动成面。
6. 如图所示的图形是由直角三角形和长方形拼成的,将该图形绕直线 $ l $ 旋转一周,求所得立体图形的体积.


答案:【解析】:本题主要考查了点、线、面、体之间的转换,以及圆锥和圆柱的体积计算。
由图可知,该图形绕直线$l$旋转一周后形成的立体图形是由一个底面半径为$3$,高为$4$的圆柱和一个底面半径为$3$,高为$2$的圆锥组成的。
根据圆柱的体积公式$V_1 = \pi r^2h_1$(其中$r$为底面半径,$h_1$为高),可得圆柱的体积为:
$V_1 = \pi × 3^2 × 4 = 36\pi$,
根据圆锥的体积公式$V_2 = \frac{1}{3} \pi r^2h_2$(其中$r$为底面半径,$h_2$为高),可得圆锥的体积为:
$V_2 = \frac{1}{3} \pi × 3^2 × 2 = 6\pi$,
那么所得立体图形的体积$V$等于圆柱的体积$V_1$与圆锥的体积$V_2$之和,即:
$V = V_1 + V_2 = 36\pi + 6\pi = 42\pi$。
【答案】:$42\pi$。
由图可知,该图形绕直线$l$旋转一周后形成的立体图形是由一个底面半径为$3$,高为$4$的圆柱和一个底面半径为$3$,高为$2$的圆锥组成的。
根据圆柱的体积公式$V_1 = \pi r^2h_1$(其中$r$为底面半径,$h_1$为高),可得圆柱的体积为:
$V_1 = \pi × 3^2 × 4 = 36\pi$,
根据圆锥的体积公式$V_2 = \frac{1}{3} \pi r^2h_2$(其中$r$为底面半径,$h_2$为高),可得圆锥的体积为:
$V_2 = \frac{1}{3} \pi × 3^2 × 2 = 6\pi$,
那么所得立体图形的体积$V$等于圆柱的体积$V_1$与圆锥的体积$V_2$之和,即:
$V = V_1 + V_2 = 36\pi + 6\pi = 42\pi$。
【答案】:$42\pi$。
7. 如图是一个几何体的侧面展开图,这个几何体可以是 (
A.圆锥
B.圆柱
C.棱锥
D.棱柱
A
)A.圆锥
B.圆柱
C.棱锥
D.棱柱
答案:解:观察该几何体的侧面展开图,其为一个扇形。圆锥的侧面展开图是扇形,圆柱的侧面展开图是长方形,棱锥的侧面展开图是多个三角形,棱柱的侧面展开图是多个长方形。因此这个几何体可以是圆锥。
答案:A
答案:A
8. 新素养 空间观念 (2023·四川巴中)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”这六个字,还原成正方体后,与“红”字所在面相对的面上的汉字是(
A.传
B.承
C.文
D.化
D
)A.传
B.承
C.文
D.化
答案:【解析】:
本题可根据正方体展开图的相对面规律来求解。
在正方体的表面展开图中,“相间、Z端是对面”,即同一行或同一列中,相隔一个面的两个面是相对面;呈“Z”字形两端的两个面是相对面。
观察所给的正方体表面展开图,“传”与“文”是相对面,“承”与“色”是相对面,“红”与“化”是相对面。
【答案】:D
本题可根据正方体展开图的相对面规律来求解。
在正方体的表面展开图中,“相间、Z端是对面”,即同一行或同一列中,相隔一个面的两个面是相对面;呈“Z”字形两端的两个面是相对面。
观察所给的正方体表面展开图,“传”与“文”是相对面,“承”与“色”是相对面,“红”与“化”是相对面。
【答案】:D
9. 如图是一个纸盒的外表面展开图,由它折叠而成的纸盒可能是 (
B
)答案:【解析】:本题考查正方体展开图的性质。
由展开图可知,有两条对角线的面与一个空白面是对面,有斜线的面与横线面是对面,两个横线面也是对面,所以由展开图可以折成的纸盒可能是B选项。
【答案】:B
由展开图可知,有两条对角线的面与一个空白面是对面,有斜线的面与横线面是对面,两个横线面也是对面,所以由展开图可以折成的纸盒可能是B选项。
【答案】:B