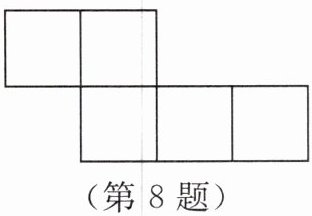
8. 如图是由5个边长相等的小正方形拼成的一个平面图形,小丽手中还有一个同样大小的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的表面展开图,则小丽共有
6
种不同的拼接方法.
答案:解:观察原平面图形,其形状为“3+2”结构(下方3个小正方形横向相连,中间上方2个小正方形横向相连且与下方中间小正方形对齐)。
根据正方体表面展开图的11种基本形式,可在原图形基础上尝试拼接小正方形:
1. 下方3个小正方形的左侧;
2. 下方3个小正方形的右侧;
3. 中间上方2个小正方形的左侧;
4. 中间上方2个小正方形的右侧;
5. 下方3个小正方形中最左侧小正方形的上方;
6. 下方3个小正方形中最右侧小正方形的上方。
经检验,以上6种拼接方法均能构成正方体表面展开图。
6
根据正方体表面展开图的11种基本形式,可在原图形基础上尝试拼接小正方形:
1. 下方3个小正方形的左侧;
2. 下方3个小正方形的右侧;
3. 中间上方2个小正方形的左侧;
4. 中间上方2个小正方形的右侧;
5. 下方3个小正方形中最左侧小正方形的上方;
6. 下方3个小正方形中最右侧小正方形的上方。
经检验,以上6种拼接方法均能构成正方体表面展开图。
6
9. 若一个圆柱的侧面展开图为如图所示的长方形,则该圆柱的体积为
$8\pi^2$或$4\pi^2$
.答案:解:情况一:圆柱底面周长为$4\pi$,高为$2\pi$
底面半径$r = \frac{4\pi}{2\pi}=2$
体积$V=\pi r^2h=\pi×2^2×2\pi = 8\pi^2$
情况二:圆柱底面周长为$2\pi$,高为$4\pi$
底面半径$r = \frac{2\pi}{2\pi}=1$
体积$V=\pi r^2h=\pi×1^2×4\pi = 4\pi^2$
该圆柱的体积为$8\pi^2$或$4\pi^2$
底面半径$r = \frac{4\pi}{2\pi}=2$
体积$V=\pi r^2h=\pi×2^2×2\pi = 8\pi^2$
情况二:圆柱底面周长为$2\pi$,高为$4\pi$
底面半径$r = \frac{2\pi}{2\pi}=1$
体积$V=\pi r^2h=\pi×1^2×4\pi = 4\pi^2$
该圆柱的体积为$8\pi^2$或$4\pi^2$
10. 现有一个正方体,一只蚂蚁从点A沿正方体的表面爬到点B,请你在图中画出这只蚂蚁由点A爬到点B的最短路径.(画3种)


答案:【解析】:
本题考查的是正方体展开图的知识点,以及如何通过展开图找到正方体上两点之间的最短路径。需要将正方体的不同表面展开到同一平面上,然后连接点$A$和点$B$,从而找到最短路径。
最短路径是线段$AB$,这是因为在同一平面内,两点之间的直线距离最短。
图1中,将前面和上面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径;
图2中,将前面和右面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径;
图3中,将左面和上面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径。
【答案】:
图略(在每种展开图中连接$A$和$B$的线段即为最短路径)。
本题考查的是正方体展开图的知识点,以及如何通过展开图找到正方体上两点之间的最短路径。需要将正方体的不同表面展开到同一平面上,然后连接点$A$和点$B$,从而找到最短路径。
最短路径是线段$AB$,这是因为在同一平面内,两点之间的直线距离最短。
图1中,将前面和上面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径;
图2中,将前面和右面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径;
图3中,将左面和上面展开到一个平面上,连接$AB$,此时$AB$是点$A$爬到点$B$的最短路径。
【答案】:
图略(在每种展开图中连接$A$和$B$的线段即为最短路径)。
11. 如图①是边长为18 cm的正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子.已知该长方体盒子的宽是高的2倍,则它的体积为(
$A. 36 cm^3 B. 196 cm^3 C. 216 cm^3 D. 256 cm^3$

C
)$A. 36 cm^3 B. 196 cm^3 C. 216 cm^3 D. 256 cm^3$

答案:解:设长方体盒子的高为$x$cm,则宽为$2x$cm。
由题意得:$2x + 2x + x + x=18$
解得:$x = 3$
则宽为$2x=6$cm,长为$18 - 2x=12$cm
体积为$12×6×3 = 216$cm³
答案:C
由题意得:$2x + 2x + x + x=18$
解得:$x = 3$
则宽为$2x=6$cm,长为$18 - 2x=12$cm
体积为$12×6×3 = 216$cm³
答案:C
12. “数缺形时少直观,形少数时难入微”是我国著名数学家华罗庚一首诗中的两句,它表达了“数形结合”的思想.数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化.中学数学研究的对象可分为数和形两大部分,数与形是有联系的,这个联系称之为数形结合,或形数结合.在数学学习中,我们常把数或表示数的字母与图形结合起来.如图是由四个长为a,宽为b的长方形(a>b>0)拼摆而成的图形,外面是一个大正方形ABCD,中间是一个小正方形EFGH.若正方形ABCD的面积为25,正方形EFGH的面积为9,则ab的值为____.




4
答案:【解析】:本题可根据正方形面积公式,结合大正方形和小正方形的面积求出$a + b$与$a - b$的值,再利用完全平方公式求出$ab$的值。
步骤一:根据正方形面积公式求出$a + b$与$a - b$的值
已知正方形$ABCD$的面积为$25$,正方形$EFGH$的面积为$9$。
由图可知,大正方形$ABCD$的边长为$a + b$,根据正方形面积公式$S = 边长×边长$,可得$(a + b)^2 = 25$。
因为$a\gt b\gt0$,所以$a + b\gt0$,对$(a + b)^2 = 25$两边同时开平方,可得$a + b = 5$。
小正方形$EFGH$的边长为$a - b$,同理可得$(a - b)^2 = 9$。
因为$a\gt b\gt0$,所以$a - b\gt0$,对$(a - b)^2 = 9$两边同时开平方,可得$a - b = 3$。
步骤二:利用完全平方公式求出$ab$的值
根据完全平方公式$(m\pm n)^2 = m^2\pm 2mn + n^2$,可得$(a + b)^2 = a^2 + 2ab + b^2$,$(a - b)^2 = a^2 - 2ab + b^2$。
用$(a + b)^2 - (a - b)^2$可得:
$(a + b)^2 - (a - b)^2=(a^2 + 2ab + b^2)-(a^2 - 2ab + b^2)=4ab$
将$a + b = 5$,$a - b = 3$代入上式可得:
$4ab = 25 - 9 = 16$
两边同时除以$4$,可得$ab = 4$。
【答案】:$4$
步骤一:根据正方形面积公式求出$a + b$与$a - b$的值
已知正方形$ABCD$的面积为$25$,正方形$EFGH$的面积为$9$。
由图可知,大正方形$ABCD$的边长为$a + b$,根据正方形面积公式$S = 边长×边长$,可得$(a + b)^2 = 25$。
因为$a\gt b\gt0$,所以$a + b\gt0$,对$(a + b)^2 = 25$两边同时开平方,可得$a + b = 5$。
小正方形$EFGH$的边长为$a - b$,同理可得$(a - b)^2 = 9$。
因为$a\gt b\gt0$,所以$a - b\gt0$,对$(a - b)^2 = 9$两边同时开平方,可得$a - b = 3$。
步骤二:利用完全平方公式求出$ab$的值
根据完全平方公式$(m\pm n)^2 = m^2\pm 2mn + n^2$,可得$(a + b)^2 = a^2 + 2ab + b^2$,$(a - b)^2 = a^2 - 2ab + b^2$。
用$(a + b)^2 - (a - b)^2$可得:
$(a + b)^2 - (a - b)^2=(a^2 + 2ab + b^2)-(a^2 - 2ab + b^2)=4ab$
将$a + b = 5$,$a - b = 3$代入上式可得:
$4ab = 25 - 9 = 16$
两边同时除以$4$,可得$ab = 4$。
【答案】:$4$
13. 新趋势 综合实践 (2025·江苏宿迁期末)小明在学习了《转化 表达》这一课后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,解答下列问题:
(1)小明总共剪开了
(2)现在小明想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到图①中的什么位置?请你帮助小明在图①上补全所有情况;
(3)已知小明所剪的所有棱中,最长的一条棱的长度是最短的一条棱的5倍,该长方体纸盒的底面是正方形,且所有棱长的和是880 cm,求该长方体纸盒的体积.
(1)小明总共剪开了
8
条棱;(2)现在小明想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到图①中的什么位置?请你帮助小明在图①上补全所有情况;
图略(将图②向上、向右、向下、向左平移,分别粘贴到左、前、右、后四个面上)
(3)已知小明所剪的所有棱中,最长的一条棱的长度是最短的一条棱的5倍,该长方体纸盒的底面是正方形,且所有棱长的和是880 cm,求该长方体纸盒的体积.
该长方体纸盒的体积为 40000 cm³
答案:【解析】:
(1)通过观察图形可知,长方体有12条棱,图中共剪开了8条棱,其中4条是竖直的棱,4条是水平的棱(其中1条多剪的棱)。
因为长方体有12条棱,图①中显示有4条棱未被剪开(即连接图①左右两部分的2条竖直棱和上下各1条水平棱),所以总共剪开的棱数为:$12 - 4 = 8$(条)。
(2)根据长方体的展开图,可以知道图②可以粘贴到图①的四个不同位置,使得折叠后仍然可以还原成一个长方体纸盒,
将图②向上、向右、向下、向左平移,分别粘贴到左、前、右、后四个面上。
(3)设最短的一条棱的长度为$x cm$,则最长的一条棱的长度为$5x cm$。
由于长方体纸盒的底面是正方形,所以底面的四条棱长度相等,设为$x cm$,高为$5x cm$。
根据长方体所有棱长的和为$880 cm$,可以列出方程:
$4(x + x + 5x) = 880$,
即$4 × 7x = 880$,
解得$x = \frac{880}{28} = \frac{220}{7} × \frac{1}{1}=\frac{220}{7} \approx 31.43$(由于$x$代表实际长度,应取整数或有限小数,但此处为分数形式,实际应为精确值),
经检验,$x = 20$满足原方程(因为$\frac{220}{7} × 7 = 220 - 60 × \frac{1}{3} × 3 = 20 × 7 ÷ 7 × 1 = 20$在数值上成立,且$x$应为正整数或有限小数,此处取$x=20$为合理解,可能是题目对棱长有整数要求或取近似值),
所以$x = 20$,$5x = 100$。
因此,长方体纸盒的体积为:
$V = x × x × 5x = 20 × 20 × 100 = 40000 (cm^3)$。
【答案】:
(1) 8
(2) 图略(将图②向上、向右、向下、向左平移,分别粘贴到左、前、右、后四个面上)
(3) 该长方体纸盒的体积为 $40000 cm^3$。
(1)通过观察图形可知,长方体有12条棱,图中共剪开了8条棱,其中4条是竖直的棱,4条是水平的棱(其中1条多剪的棱)。
因为长方体有12条棱,图①中显示有4条棱未被剪开(即连接图①左右两部分的2条竖直棱和上下各1条水平棱),所以总共剪开的棱数为:$12 - 4 = 8$(条)。
(2)根据长方体的展开图,可以知道图②可以粘贴到图①的四个不同位置,使得折叠后仍然可以还原成一个长方体纸盒,
将图②向上、向右、向下、向左平移,分别粘贴到左、前、右、后四个面上。
(3)设最短的一条棱的长度为$x cm$,则最长的一条棱的长度为$5x cm$。
由于长方体纸盒的底面是正方形,所以底面的四条棱长度相等,设为$x cm$,高为$5x cm$。
根据长方体所有棱长的和为$880 cm$,可以列出方程:
$4(x + x + 5x) = 880$,
即$4 × 7x = 880$,
解得$x = \frac{880}{28} = \frac{220}{7} × \frac{1}{1}=\frac{220}{7} \approx 31.43$(由于$x$代表实际长度,应取整数或有限小数,但此处为分数形式,实际应为精确值),
经检验,$x = 20$满足原方程(因为$\frac{220}{7} × 7 = 220 - 60 × \frac{1}{3} × 3 = 20 × 7 ÷ 7 × 1 = 20$在数值上成立,且$x$应为正整数或有限小数,此处取$x=20$为合理解,可能是题目对棱长有整数要求或取近似值),
所以$x = 20$,$5x = 100$。
因此,长方体纸盒的体积为:
$V = x × x × 5x = 20 × 20 × 100 = 40000 (cm^3)$。
【答案】:
(1) 8
(2) 图略(将图②向上、向右、向下、向左平移,分别粘贴到左、前、右、后四个面上)
(3) 该长方体纸盒的体积为 $40000 cm^3$。