1. 一条公路,第一天修了20%,第二天比第一天少修300米,还剩75%没有修。求公路全长。
答案:1-75%-20%=5% 300÷(20%-5%)=2000(米)
2. 印刷厂为一款燕麦片设计包装盒,图纸如下。这款包装盒的表面积、容积各是多少?
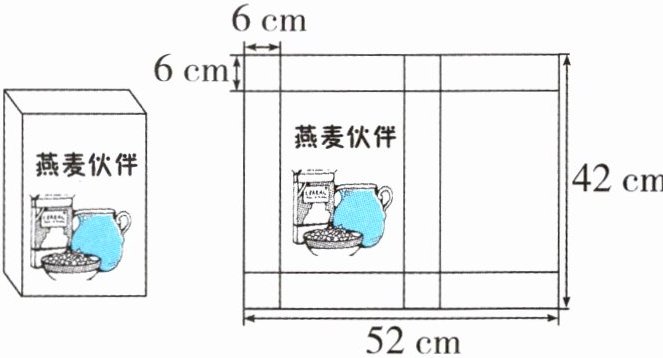

答案:高:42-6×2=30(厘米) 长:52÷2-6=20(厘米) 表面积:(30×20+30×6+20×6)×2=1800(平方厘米) 容积:30×20×6=3600(立方厘米)
解析:
高:$42 - 6×2 = 30$(厘米)
长:$52÷2 - 6 = 20$(厘米)
表面积:$(30×20 + 30×6 + 20×6)×2 = 1800$(平方厘米)
容积:$30×20×6 = 3600$(立方厘米)
长:$52÷2 - 6 = 20$(厘米)
表面积:$(30×20 + 30×6 + 20×6)×2 = 1800$(平方厘米)
容积:$30×20×6 = 3600$(立方厘米)
3. 佳惠超市按商品的标价打八折进行促销,光明小学在此超市按促销价购买了200支钢笔,共付2040元。如果每支钢笔的进价是8.5元,超市是在进价基础上加价百分之几将这200支钢笔卖给光明小学的?
答案:(2040÷200-8.5)÷8.5=20%
解析:
2040÷200=10.2(元)
10.2-8.5=1.7(元)
1.7÷8.5=0.2=20%
答:超市是在进价基础上加价20%将这200支钢笔卖给光明小学的。
10.2-8.5=1.7(元)
1.7÷8.5=0.2=20%
答:超市是在进价基础上加价20%将这200支钢笔卖给光明小学的。
4. 在一个长50厘米、宽30厘米、高24厘米的长方体容器中装满水,平放在桌上,现在把它斜放,水倒出$\frac{3}{8}$,这时AB的长度是多少厘米?


答案:50×30×24×$\frac{3}{8}$×2÷(50×30)=18(厘米)
5. 甲、乙两瓶油共480毫升,从甲瓶中倒出它的20%给乙瓶后,甲、乙两瓶中油的体积之比是5:3,甲瓶中原有油多少毫升?
答案:480÷(3+5)×5=300(毫升) 300÷(1-20%)=375(毫升)
解析:
480÷(5+3)×5=300(毫升)
300÷(1-20%)=375(毫升)
答:甲瓶中原有油375毫升。
300÷(1-20%)=375(毫升)
答:甲瓶中原有油375毫升。
6. 常温下,含盐率大于26.5%的盐水会出现盐结晶的现象。科学课上老师在准备“盐的结晶”实验时,配制了120克的盐水,其中盐和水的质量比是1:4,老师将盐水加热、沸腾(蒸发),当剩下的盐水重80克时,冷却至常温,这时盐水中会出现盐结晶现象吗?
答案:120÷(1+4)×1=24(克) 24÷80=0.3=30% 30%>26.5% 会出现盐结晶现象 提示:将盐水加热、沸腾(蒸发),不会影响盐水中盐的质量,加热、蒸发前盐与水的质量比是1:4,先求出盐的质量,再用盐的质量除以加热后盐水的质量,求得加热、沸腾(蒸发)、冷却至常温后盐水的含盐率,再与26.5%比较即可。
解析:
120÷(1+4)×1=24(克)
24÷80=0.3=30%
30%>26.5%
会出现盐结晶现象
24÷80=0.3=30%
30%>26.5%
会出现盐结晶现象
7. 60名学生参加环保活动,每个男生捡2千克垃圾,每个女生捡1.6千克垃圾。男生中抽出20%的人负责收集和运送垃圾,其他的同学捡垃圾。这60名学生一共捡了多少千克垃圾?
答案:2×(1-20%)=1.6(千克) 60×1.6=96(千克) 提示:不管男生有多少人,抽出男生的20%,男生实际捡的垃圾总量比计划少20%,因此平均每个男生少捡计划量的20%。每个男生捡2千克,实际上平均每个男生只捡了2×(1-20%)=1.6(千克),正好和女生每人捡的一样多。
解析:
2×(1-20%)=1.6(千克)
60×1.6=96(千克)
答:这60名学生一共捡了96千克垃圾。
60×1.6=96(千克)
答:这60名学生一共捡了96千克垃圾。
强基直通车 有一次考试,考生中男生人数是总人数的$\frac{4}{7}$,结果录取91人,其中男生与女生人数之比是8:5。在未被录取的学生中,男生人数是未录取人数的$\frac{3}{7}$。那么报考的总人数是多少?
答案:录取的学生中男生有91×$\frac{8}{5+8}$=56(人),设报考的总人数是x人,则未被录取的学生有(x-91)人,根据未被录取的男生人数可列方程为$\frac{4}{7}$x-56=(x-91)×$\frac{3}{7}$,解得x=119。 提示:先根据“结果录取91人,其中男生与女生人数之比是8:5”,利用按比分配的方法求出录取的男生人数,则未被录取的男生人数,既可以用“男生总人数-已经被录取的男生人数”表示,也可以用“未被录取的学生数×$\frac{3}{7}$”表示,所以可以列出等量关系“男生总人数-已经被录取的男生人数=未被录取的学生数×$\frac{3}{7}$”。再设报考的总人数是x人,列方程即可求出报考的总人数是119人。
解析:
录取的男生人数为:$91×\frac{8}{8+5}=91×\frac{8}{13}=56$(人)
设报考的总人数是$x$人,则未被录取的学生人数为$(x - 91)$人。
男生总人数为$\frac{4}{7}x$,未被录取的男生人数为$\frac{4}{7}x - 56$。
又因为未被录取的男生人数是未录取人数的$\frac{3}{7}$,所以可列方程:
$\frac{4}{7}x - 56 = \frac{3}{7}(x - 91)$
方程两边同时乘以$7$得:
$4x - 392 = 3(x - 91)$
展开括号:
$4x - 392 = 3x - 273$
移项:
$4x - 3x = 392 - 273$
解得:
$x = 119$
报考的总人数是$119$人。
设报考的总人数是$x$人,则未被录取的学生人数为$(x - 91)$人。
男生总人数为$\frac{4}{7}x$,未被录取的男生人数为$\frac{4}{7}x - 56$。
又因为未被录取的男生人数是未录取人数的$\frac{3}{7}$,所以可列方程:
$\frac{4}{7}x - 56 = \frac{3}{7}(x - 91)$
方程两边同时乘以$7$得:
$4x - 392 = 3(x - 91)$
展开括号:
$4x - 392 = 3x - 273$
移项:
$4x - 3x = 392 - 273$
解得:
$x = 119$
报考的总人数是$119$人。