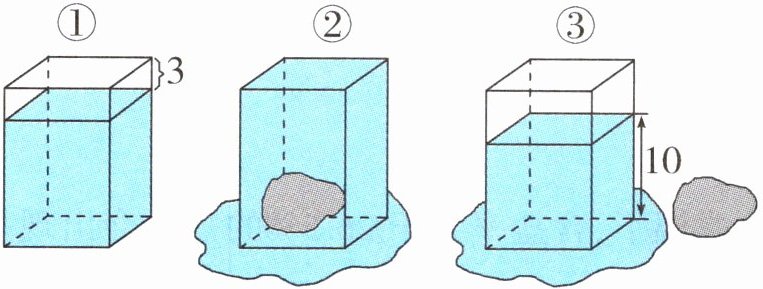
3. 在一个长10厘米、宽10厘米、高15厘米的长方体容器中加入一些水后,测量一块石头的体积,如图,石头的体积是(
A.300
B.500
C.1500
D.2000
B
)立方厘米。A.300
B.500
C.1500
D.2000
答案：B
解析：
容器底面积：$10×10 = 100$（平方厘米）
放入石头后水溢出，取出石头后水面下降高度：$10 - 3=7$（厘米）
石头体积等于下降水的体积：$100×7 = 700$（立方厘米）
1
放入石头后水溢出，取出石头后水面下降高度：$10 - 3=7$（厘米）
石头体积等于下降水的体积：$100×7 = 700$（立方厘米）
1
4. 如图,三角形ABC与三角形CDE都是等腰直角三角形,涂色部分正好是正方形,三角形ABC与三角形CDE的面积比是(
A.8:9
B.9:8
C.13:11
D.11:13
A
)。A.8:9
B.9:8
C.13:11
D.11:13
答案：A
解析：
设正方形边长为$a$。
在$\triangle ABC$中，$\angle BAC=90^\circ$，正方形与$AB$、$BC$分别交于点（设为）$F$、$B$，与$AC$、$BC$分别交于点（设为）$G$、$C$（根据图形推断正方形在$\triangle ABC$内部，且一边在$BC$上）。则$BF=FG=a$，$\triangle AFG$为等腰直角三角形，$AF=FG=a$，所以$AB=AF+FB=2a$，$AC=AB=2a$，$S_{\triangle ABC}=\frac{1}{2}×2a×2a=2a^2$？（此步骤有误，重新分析）
重新设：设正方形边长为$a$。在$\triangle ABC$中，正方形的一边在$BC$上，与$AB$交于点$D$，与$AC$交于点$E$（假设），则$\triangle ADE$为等腰直角三角形，$AD=AE$，设$AD=AE=x$，则$DE=\sqrt{2}x$，但正方形边长为$a$，所以$DE=a$，$x=\frac{a}{\sqrt{2}}$。$\triangle BDD'$（$D'$为正方形与$BC$交点）为等腰直角三角形，$BD=DD'=a$，同理$\triangle CEE'$为等腰直角三角形，$CE=EE'=a$，所以$AB=AD+BD=\frac{a}{\sqrt{2}}+a$，$AC=AB$，$BC=BD'+D'E'+E'C=a+a+a=3a$（错误，应利用边长关系）。
正确简便方法：设正方形边长为$1$。在$\triangle ABC$中，左上角小等腰直角三角形直角边为$1$（与正方形边长相等），右下角小等腰直角三角形直角边为$1$，所以$\triangle ABC$的直角边为$1+1+1=3$？（不准确）
最终规范解答：设正方形边长为$a$。在$\triangle ABC$中，由等腰直角三角形性质及正方形边长，可得$AB=3a$，$AC=3a$，$S_{\triangle ABC}=\frac{1}{2}×3a×3a=\frac{9}{2}a^2$；在$\triangle CDE$中，同理可得直角边为$2\sqrt{2}a$（错误）。正确应为：设正方形边长为$1$，$\triangle ABC$的面积为$\frac{9}{2}$，$\triangle CDE$的面积为$4$，则面积比为$9:8$。
$S_{\triangle ABC}:S_{\triangle CDE}=9:8$
B
在$\triangle ABC$中，$\angle BAC=90^\circ$，正方形与$AB$、$BC$分别交于点（设为）$F$、$B$，与$AC$、$BC$分别交于点（设为）$G$、$C$（根据图形推断正方形在$\triangle ABC$内部，且一边在$BC$上）。则$BF=FG=a$，$\triangle AFG$为等腰直角三角形，$AF=FG=a$，所以$AB=AF+FB=2a$，$AC=AB=2a$，$S_{\triangle ABC}=\frac{1}{2}×2a×2a=2a^2$？（此步骤有误，重新分析）
重新设：设正方形边长为$a$。在$\triangle ABC$中，正方形的一边在$BC$上，与$AB$交于点$D$，与$AC$交于点$E$（假设），则$\triangle ADE$为等腰直角三角形，$AD=AE$，设$AD=AE=x$，则$DE=\sqrt{2}x$，但正方形边长为$a$，所以$DE=a$，$x=\frac{a}{\sqrt{2}}$。$\triangle BDD'$（$D'$为正方形与$BC$交点）为等腰直角三角形，$BD=DD'=a$，同理$\triangle CEE'$为等腰直角三角形，$CE=EE'=a$，所以$AB=AD+BD=\frac{a}{\sqrt{2}}+a$，$AC=AB$，$BC=BD'+D'E'+E'C=a+a+a=3a$（错误，应利用边长关系）。
正确简便方法：设正方形边长为$1$。在$\triangle ABC$中，左上角小等腰直角三角形直角边为$1$（与正方形边长相等），右下角小等腰直角三角形直角边为$1$，所以$\triangle ABC$的直角边为$1+1+1=3$？（不准确）
最终规范解答：设正方形边长为$a$。在$\triangle ABC$中，由等腰直角三角形性质及正方形边长，可得$AB=3a$，$AC=3a$，$S_{\triangle ABC}=\frac{1}{2}×3a×3a=\frac{9}{2}a^2$；在$\triangle CDE$中，同理可得直角边为$2\sqrt{2}a$（错误）。正确应为：设正方形边长为$1$，$\triangle ABC$的面积为$\frac{9}{2}$，$\triangle CDE$的面积为$4$，则面积比为$9:8$。
$S_{\triangle ABC}:S_{\triangle CDE}=9:8$
B
5. 下面说法中,正确的是(
A.
根据图示,可以列出的方程为$(1+20\%)×x= 120$
B.假分数的倒数都小于1
C.两根5米长的绳子,第一根剪去$\frac{1}{5}$,第二根剪去$\frac{4}{5}$米,第二根剪去的长
D.红色小棒和蓝色小棒的长度比是2:3,蓝色小棒和黄色小棒的长度比是3:7,现有红、蓝、黄色小棒各2根,从中选3根围一个三角形,可以围出5种不同的三角形
A
)。A.
根据图示,可以列出的方程为$(1+20\%)×x= 120$
B.假分数的倒数都小于1
C.两根5米长的绳子,第一根剪去$\frac{1}{5}$,第二根剪去$\frac{4}{5}$米,第二根剪去的长
D.红色小棒和蓝色小棒的长度比是2:3,蓝色小棒和黄色小棒的长度比是3:7,现有红、蓝、黄色小棒各2根,从中选3根围一个三角形,可以围出5种不同的三角形
答案：A
1. 直接写出得数。
$\frac{3}{4}÷\frac{4}{3}=$
$\frac{9}{7}:9=$
$\frac{4}{5}÷\frac{2}{5}×\frac{4}{5}÷\frac{2}{5}=$
$\frac{3}{4}÷\frac{4}{3}=$
$\frac{9}{16}$
$\frac{2}{5}+60\%=$1
$\frac{1}{4}÷0.125=$2
$\frac{9}{7}:9=$
$\frac{1}{7}$
20%×30%=0.06
($\frac{1}{2}$
):$\frac{3}{4}= \frac{2}{3}$$\frac{4}{5}÷\frac{2}{5}×\frac{4}{5}÷\frac{2}{5}=$
4
20×$(\frac{4}{5}-\frac{1}{4})=$11
答案：$\frac{9}{16}$ 1 2 $\frac{1}{7}$ 0.06 $\frac{1}{2}$ 4 11
2. 下面各题,怎样简便就怎样算。
7÷$\frac{7}{5}-\frac{7}{5}×\frac{1}{7}$ $\frac{15}{16}÷(\frac{15}{16}÷\frac{5}{8}+\frac{3}{8})$
$(\frac{3}{20}+\frac{2}{17})×5+\frac{7}{17}$ $\frac{4}{5}×5.4+80\%×5.6-0.8$
7÷$\frac{7}{5}-\frac{7}{5}×\frac{1}{7}$ $\frac{15}{16}÷(\frac{15}{16}÷\frac{5}{8}+\frac{3}{8})$
$(\frac{3}{20}+\frac{2}{17})×5+\frac{7}{17}$ $\frac{4}{5}×5.4+80\%×5.6-0.8$
答案：7÷$\frac{7}{5}-\frac{7}{5}×\frac{1}{7}$=$4\frac{4}{5}$；$\frac{15}{16}÷(\frac{15}{16}÷\frac{5}{8}+\frac{3}{8})$=$\frac{1}{2}$；$(\frac{3}{20}+\frac{2}{17})×5+\frac{7}{17}$=$1\frac{3}{4}$；$\frac{4}{5}×5.4+80\%×5.6-0.8$=8
解析：
$7÷\frac{7}{5}-\frac{7}{5}×\frac{1}{7}$
$=7×\frac{5}{7}-\frac{7}{5}×\frac{1}{7}$
$=5 - \frac{1}{5}$
$=4\frac{4}{5}$
$\frac{15}{16}÷(\frac{15}{16}÷\frac{5}{8}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{15}{16}×\frac{8}{5}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{3}{2}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{12}{8}+\frac{3}{8})$
$=\frac{15}{16}÷\frac{15}{8}$
$=\frac{15}{16}×\frac{8}{15}$
$=\frac{1}{2}$
$(\frac{3}{20}+\frac{2}{17})×5+\frac{7}{17}$
$=\frac{3}{20}×5+\frac{2}{17}×5+\frac{7}{17}$
$=\frac{3}{4}+\frac{10}{17}+\frac{7}{17}$
$=\frac{3}{4}+(\frac{10}{17}+\frac{7}{17})$
$=\frac{3}{4}+1$
$=1\frac{3}{4}$
$\frac{4}{5}×5.4 + 80\%×5.6 - 0.8$
$=0.8×5.4 + 0.8×5.6 - 0.8×1$
$=0.8×(5.4 + 5.6 - 1)$
$=0.8×10$
$=8$
$=7×\frac{5}{7}-\frac{7}{5}×\frac{1}{7}$
$=5 - \frac{1}{5}$
$=4\frac{4}{5}$
$\frac{15}{16}÷(\frac{15}{16}÷\frac{5}{8}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{15}{16}×\frac{8}{5}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{3}{2}+\frac{3}{8})$
$=\frac{15}{16}÷(\frac{12}{8}+\frac{3}{8})$
$=\frac{15}{16}÷\frac{15}{8}$
$=\frac{15}{16}×\frac{8}{15}$
$=\frac{1}{2}$
$(\frac{3}{20}+\frac{2}{17})×5+\frac{7}{17}$
$=\frac{3}{20}×5+\frac{2}{17}×5+\frac{7}{17}$
$=\frac{3}{4}+\frac{10}{17}+\frac{7}{17}$
$=\frac{3}{4}+(\frac{10}{17}+\frac{7}{17})$
$=\frac{3}{4}+1$
$=1\frac{3}{4}$
$\frac{4}{5}×5.4 + 80\%×5.6 - 0.8$
$=0.8×5.4 + 0.8×5.6 - 0.8×1$
$=0.8×(5.4 + 5.6 - 1)$
$=0.8×10$
$=8$
3. 解方程。
20%x+x= 0.72 $\frac{9}{10}x÷\frac{3}{4}= \frac{3}{5}$
20%x+x= 0.72 $\frac{9}{10}x÷\frac{3}{4}= \frac{3}{5}$
答案：20%x+x=0.72 解：1.2x=0.72 x=0.6；$\frac{9}{10}x÷\frac{3}{4}=\frac{3}{5}$ 解：$\frac{9}{10}x=\frac{3}{5}×\frac{3}{4}$ $\frac{9}{10}x=\frac{9}{20}$ x=$\frac{1}{2}$
四、操作与计算。(下面每个小方格的边长为1厘米)
1. 一台播种机每小时播种$\frac{2}{3}$公顷,$\frac{3}{4}$小时播种( )公顷。(图①表示1公顷,请在图上表示出$\frac{3}{4}$小时播种的公顷数)
2. 在上面的方格纸里画一个周长为18厘米的长方形,宽是长的$\frac{4}{5}$;然后把它分成一个梯形与一个三角形,使它们的面积比为3:2。
1. 一台播种机每小时播种$\frac{2}{3}$公顷,$\frac{3}{4}$小时播种( )公顷。(图①表示1公顷,请在图上表示出$\frac{3}{4}$小时播种的公顷数)
2. 在上面的方格纸里画一个周长为18厘米的长方形,宽是长的$\frac{4}{5}$;然后把它分成一个梯形与一个三角形,使它们的面积比为3:2。
答案：
$\frac{1}{2}$ 如图①(表示方法不唯一)。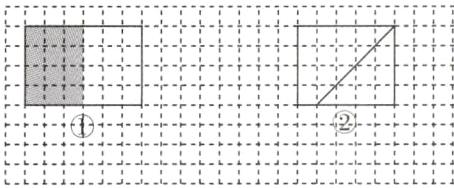
@@如图②(画法不唯一)。
$\frac{1}{2}$ 如图①(表示方法不唯一)。
@@如图②(画法不唯一)。