7. 一个长方形的宽比长短$\frac {1}{4}$,如果把宽延长2厘米,就变成一个正方形,求长方形的面积。
答案:7.设长是x厘米。 $\frac{1}{4}x=2$ $x=8$ $8 - 2 = 6$(厘米)$8×6 = 48$(平方厘米) 提示:“把宽延长2厘米,就变成一个正方形”说明宽比长短2厘米,即长的$\frac{1}{4}$就是2厘米,设长是x厘米,可列方程为$\frac{1}{4}x=2$,$x=8$,所以宽为$8 - 2 = 6$(厘米),长方形的面积为$8×6 = 48$(平方厘米)。
解析:
设长是$x$厘米。
$\frac{1}{4}x = 2$
$x = 8$
宽:$8 - 2 = 6$(厘米)
面积:$8×6 = 48$(平方厘米)
$\frac{1}{4}x = 2$
$x = 8$
宽:$8 - 2 = 6$(厘米)
面积:$8×6 = 48$(平方厘米)
8. 2路公交车出发时车上有4个空座位,中途第一次停站时,车上有$\frac {1}{5}$的乘客下车,上车10人,这时座位正好坐满。车上原来有多少位乘客?车上一共有多少个座位?
答案:8.$10 - 4 = 6$(位) 设原来车上有x位乘客。$\frac{1}{5}x=6$ $x=30$ $30 + 4 = 34$(个) 提示:根据题意可知,$(10 - 4)$位乘客占原来车上乘客人数的$\frac{1}{5}$,设原来车上有x位乘客,可列方程为$\frac{1}{5}x=6$,$x=30$。出发时车上有4个空座位,所以车上一共有$30 + 4 = 34$(个)座位。
解析:
设原来车上有$x$位乘客。
$10 - 4 = 6$(位)
$\frac{1}{5}x = 6$
$x = 30$
座位数:$30 + 4 = 34$(个)
答:车上原来有30位乘客,车上一共有34个座位。
$10 - 4 = 6$(位)
$\frac{1}{5}x = 6$
$x = 30$
座位数:$30 + 4 = 34$(个)
答:车上原来有30位乘客,车上一共有34个座位。
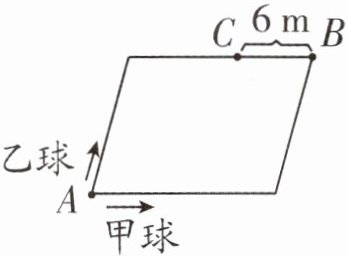
9. 如图,在一个平行四边形轨道上,甲球和乙球同时从点A分别向不同的方向出发,40秒后在点C处相遇,已知乙球行的路程是甲球的$\frac {5}{8}$,求甲球每秒行多少米。
]
]

答案:9.$6×2 = 12$(米) $1 - \frac{5}{8}=\frac{3}{8}$ 设甲球所行的路程是x米。 $\frac{3}{8}x=12$ $x=32$ $32÷40 = 0.8$(米)提示:从题图中可以看出,乙球比甲球少行了$6×2 = 12$(米),由于“乙球行的路程是甲球的$\frac{5}{8}$”,则乙球比甲球少行的12米占甲球所行路程的$1 - \frac{5}{8}=\frac{3}{8}$。设甲球所行的路程是x米,可列方程为$\frac{3}{8}x=12$,$x=32$。所以甲球每秒行$32÷40 = 0.8$(米)。
解析:
$6×2 = 12$(米)
$1-\frac{5}{8}=\frac{3}{8}$
设甲球所行的路程是$x$米。
$\frac{3}{8}x=12$
$x=32$
$32÷40 = 0.8$(米)
答:甲球每秒行$0.8$米。
$1-\frac{5}{8}=\frac{3}{8}$
设甲球所行的路程是$x$米。
$\frac{3}{8}x=12$
$x=32$
$32÷40 = 0.8$(米)
答:甲球每秒行$0.8$米。
10. 一根绳子,第一次用去$\frac {3}{5}$米,第二次用去余下的$\frac {3}{5}$,两次共用去6米。这根绳子原来长多少米?
答案:10.设第一次用去后绳子余下x米。$\frac{3}{5}x=6 - \frac{3}{5}$ $x=9$ $9+\frac{3}{5}=9\frac{3}{5}$(米) 提示:第二次用去$(6 - \frac{3}{5})$米,根据第一次用去后余下的米数$×\frac{3}{5}=$第二次用去的米数这一数量关系式,可求出第一次用去后余下的米数,然后加上第一次用去的米数,便得到这根绳子原来的长度。
解析:
设第一次用去后绳子余下$x$米。
$\frac{3}{5}x = 6 - \frac{3}{5}$
$\frac{3}{5}x = \frac{27}{5}$
$x = 9$
$9 + \frac{3}{5} = \frac{48}{5}$(米)
答:这根绳子原来长$\frac{48}{5}$米。
$\frac{3}{5}x = 6 - \frac{3}{5}$
$\frac{3}{5}x = \frac{27}{5}$
$x = 9$
$9 + \frac{3}{5} = \frac{48}{5}$(米)
答:这根绳子原来长$\frac{48}{5}$米。
11. 甲、乙两车同时从A地匀速开往B地,当甲车行了全程的$\frac {1}{3}$时,乙车正好行了60千米;当甲车到达B地时,乙车行了全程的$\frac {3}{5}$。A、B两地相距多少千米?
答案:11.设A、B两地相距x千米。 $\frac{3}{5}x=3×60$ $x=300$ 提示:当甲车行了全程的$\frac{1}{3}$时,乙车正好行了60千米。甲车到达B地时,即甲车已行完全程,那么乙车就行了3个60千米,也就是180千米,是全程的$\frac{3}{5}$。
解析:
设A、B两地相距$x$千米。
当甲车到达B地时,甲车行驶的路程是开始时的$1÷\frac{1}{3}=3$倍,此时乙车行驶的路程为$3×60 = 180$千米。
已知此时乙车行了全程的$\frac{3}{5}$,则$\frac{3}{5}x=180$,解得$x = 300$。
答:A、B两地相距300千米。
当甲车到达B地时,甲车行驶的路程是开始时的$1÷\frac{1}{3}=3$倍,此时乙车行驶的路程为$3×60 = 180$千米。
已知此时乙车行了全程的$\frac{3}{5}$,则$\frac{3}{5}x=180$,解得$x = 300$。
答:A、B两地相距300千米。
12. 有甲、乙两袋大米,甲袋比乙袋少24千克。如果再从甲袋盛6千克大米倒入乙袋,这时甲袋大米的质量相当于乙袋的$\frac {5}{8}$。两袋大米原来各有多少千克?
答案:12.设乙袋大米现在有x千克。 $(1 - \frac{5}{8})x=24 + 6×2$ $x=96$ 原来乙袋大米:$96 - 6 = 90$(千克)原来甲袋大米:$90 - 24 = 66$(千克) 提示:根据题意可以画出如图所示的线段图,从图中可以看出,现在甲袋大米比乙袋大米少$(24 + 6×2)$千克,占乙袋大米的$(1 - \frac{5}{8})$,根据现在乙袋大米的质量$×(1 - \frac{5}{8})=24 + 6×2$这一数量关系式,先求出乙袋大米现在的质量,再减去6千克,求出乙袋大米原来的质量,最后再求出甲袋大米原来的质量。
解析:
设乙袋大米现在有$x$千克。
$(1 - \frac{5}{8})x = 24 + 6×2$
$\frac{3}{8}x = 36$
$x = 96$
原来乙袋大米:$96 - 6 = 90$(千克)
原来甲袋大米:$90 - 24 = 66$(千克)
答:甲袋原来有66千克,乙袋原来有90千克。
$(1 - \frac{5}{8})x = 24 + 6×2$
$\frac{3}{8}x = 36$
$x = 96$
原来乙袋大米:$96 - 6 = 90$(千克)
原来甲袋大米:$90 - 24 = 66$(千克)
答:甲袋原来有66千克,乙袋原来有90千克。