6. 知识迁移 下面小正方体的棱长都是1厘米。
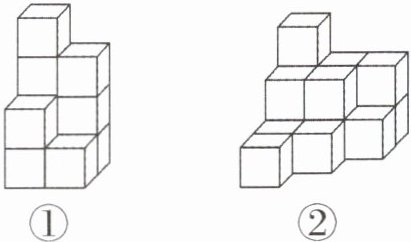
立体图形①的表面积$=(4+7+6)×2$,其中4、7、6分别是从上面、前面和右面观察到的图形的面积。
(1)用立体图形①的表面积的求法,求立体图形②的表面积,可以列式为____
(2)如果添加同样的正方体,把图②补充成一个长方体,这个长方体的表面积至少是(

立体图形①的表面积$=(4+7+6)×2$,其中4、7、6分别是从上面、前面和右面观察到的图形的面积。
(1)用立体图形①的表面积的求法,求立体图形②的表面积,可以列式为____
$(9 + 7 + 7)×2$
。(2)如果添加同样的正方体,把图②补充成一个长方体,这个长方体的表面积至少是(
66
)平方厘米。答案:6.
(1)$(9 + 7 + 7)×2$ 提示:从上面观察立体图形②有9个正方形,面积之和为9平方厘米,从前面观察有7个正方形,面积之和为7平方厘米,从右面观察有7个正方形,面积之和为7平方厘米,因此列式为$(9 + 7 + 7)×2$。
(2)66 提示:$(4×3 + 4×3 + 3×3)×2=66$(平方厘米)。
(1)$(9 + 7 + 7)×2$ 提示:从上面观察立体图形②有9个正方形,面积之和为9平方厘米,从前面观察有7个正方形,面积之和为7平方厘米,从右面观察有7个正方形,面积之和为7平方厘米,因此列式为$(9 + 7 + 7)×2$。
(2)66 提示:$(4×3 + 4×3 + 3×3)×2=66$(平方厘米)。
7. 如图①是一件长方体物品,把12件同样的长方体物品打包,如图②③。

(1)图②的表面积是
图③的表面积是
(2)以下三种情况时,比一比图②和图③的打包方法的表面积大小。
当$b= 2c$时,$S_{②}$○$S_{③}$;
当$b<2c$时,$S_{②}$○$S_{③}$;
当$b>2c$时,$S_{②}$○$S_{③}$。

(1)图②的表面积是
6ab + 8ac + 24bc
。图③的表面积是
4ab + 12ac + 24bc
。(2)以下三种情况时,比一比图②和图③的打包方法的表面积大小。
当$b= 2c$时,$S_{②}$○$S_{③}$;
=
当$b<2c$时,$S_{②}$○$S_{③}$;
<
当$b>2c$时,$S_{②}$○$S_{③}$。
>
答案:7.
(1)$6ab + 8ac + 24bc$ $4ab + 12ac + 24bc$ 提示:题图②中的长方体的表面积是$(a×3b + 3b×4c + a×4c)×2=6ab + 8ac + 24bc$;题图③中的长方体的表面积是$(a×2b + 2b×6c + a×6c)×2=4ab + 12ac + 24bc$。
(2)= < > 提示:将两个长方体的表面积都去掉相同的部分后,两个式子的大小要看$2ab$与$4ac$的大小。当$b = 2c$时,$2ab=4ac$,两种打包方法表面积相同;当$b<2c$时,题图②的打包方法表面积较小;当$b>2c$时,题图③的打包方法表面积较小。
(1)$6ab + 8ac + 24bc$ $4ab + 12ac + 24bc$ 提示:题图②中的长方体的表面积是$(a×3b + 3b×4c + a×4c)×2=6ab + 8ac + 24bc$;题图③中的长方体的表面积是$(a×2b + 2b×6c + a×6c)×2=4ab + 12ac + 24bc$。
(2)= < > 提示:将两个长方体的表面积都去掉相同的部分后,两个式子的大小要看$2ab$与$4ac$的大小。当$b = 2c$时,$2ab=4ac$,两种打包方法表面积相同;当$b<2c$时,题图②的打包方法表面积较小;当$b>2c$时,题图③的打包方法表面积较小。
8. (1)一个长方体的表面积是$22a^{2}$,长+宽$=5a$,长×宽$=6a^{2}$,则这个长方体的高是(
(2)乐乐将3个相同的有盖长方体垃圾箱紧挨着排成一排,表面积最多会减少2640平方厘米,最少会减少1440平方厘米。每个垃圾箱的侧面积是(
a
)。(2)乐乐将3个相同的有盖长方体垃圾箱紧挨着排成一排,表面积最多会减少2640平方厘米,最少会减少1440平方厘米。每个垃圾箱的侧面积是(
2040
)平方厘米;如果垃圾箱的高是30厘米,那么一个垃圾箱的表面积是(2568
)平方厘米。答案:8.
(1)a 提示:长方体的表面积=侧面积+底面积×2=(长+宽)$×2×$高+$6a^{2}×2=22a^{2}$,所以高=$(22a^{2}-12a^{2})÷10a=a$。
(2)2040 2568 提示:垃圾箱只能将侧面紧挨着排,3个垃圾箱紧挨着排成一排,有两种排法,如图,一种是长×高那面紧挨在一起,一种是宽×高那面紧挨在一起。不管怎么排,表面积都减少4个相同的面的面积,长×高那面的面积是$2640÷4 = 660$(平方厘米),宽×高那面的面积是$1440÷4 = 360$(平方厘米),所以每个垃圾箱的侧面积是$(660 + 360)×2=2040$(平方厘米)。如果垃圾箱的高是30厘米,那么长是$660÷30 = 22$(厘米),宽是$360÷30 = 12$(厘米),上下面的面积和是$22×12×2 = 528$(平方厘米),一个垃圾箱的表面积是$2040 + 528=2568$(平方厘米)。
(1)a 提示:长方体的表面积=侧面积+底面积×2=(长+宽)$×2×$高+$6a^{2}×2=22a^{2}$,所以高=$(22a^{2}-12a^{2})÷10a=a$。
(2)2040 2568 提示:垃圾箱只能将侧面紧挨着排,3个垃圾箱紧挨着排成一排,有两种排法,如图,一种是长×高那面紧挨在一起,一种是宽×高那面紧挨在一起。不管怎么排,表面积都减少4个相同的面的面积,长×高那面的面积是$2640÷4 = 660$(平方厘米),宽×高那面的面积是$1440÷4 = 360$(平方厘米),所以每个垃圾箱的侧面积是$(660 + 360)×2=2040$(平方厘米)。如果垃圾箱的高是30厘米,那么长是$660÷30 = 22$(厘米),宽是$360÷30 = 12$(厘米),上下面的面积和是$22×12×2 = 528$(平方厘米),一个垃圾箱的表面积是$2040 + 528=2568$(平方厘米)。
9. 一个长方体木块,如果它的高减少3分米,那么就成为一个正方体,这时它的表面积减少72平方分米。求原来长方体的表面积。
答案:9. $72÷4÷3 = 6$(分米) $6×6×6 + 72=288$(平方分米) 提示:根据题意,可画出图形。从图中可以看出,这个长方体的高减少3分米,剩下的部分是一个正方体,说明上面截去的部分是一个底面为正方形的长方体,它的前、后、左、右四个面是完全相同的长方形,所以减少的表面积相当于截去的长方体的前、后、左、右四个面(图中阴影部分)的面积和,则截去部分的底面边长为$72÷4÷3 = 6$(分米),由此即可求出原长方体的表面积。
解析:
$72÷4÷3 = 6$(分米)
$6×6×6 + 72=288$(平方分米)
答:原来长方体的表面积是288平方分米。
$6×6×6 + 72=288$(平方分米)
答:原来长方体的表面积是288平方分米。
10. 一个长方体的长为8厘米,上面与前面的面积之和为72平方厘米,右面的面积是上面的一半,求这个长方体的表面积。


答案:10. $72÷8 = 9$(厘米) 高:$8÷2 = 4$(厘米) 宽:$9 - 4 = 5$(厘米) 表面积:$8×5×2 + 8×4×2 + 5×4×2=184$(平方厘米) 提示:已知上面的面积+前面的面积=72平方厘米,那么宽与高的和为$72÷8 = 9$(厘米)。因为右面的面积是上面的一半,所以高是长的一半,即高为$8÷2 = 4$(厘米),则宽为$9 - 4 = 5$(厘米),进而求出这个长方体的表面积。
解析:
宽与高的和:$72÷8 = 9$(厘米)
高:$8÷2 = 4$(厘米)
宽:$9 - 4 = 5$(厘米)
表面积:$8×5×2 + 8×4×2 + 5×4×2$
$=80 + 64 + 40$
$=184$(平方厘米)
高:$8÷2 = 4$(厘米)
宽:$9 - 4 = 5$(厘米)
表面积:$8×5×2 + 8×4×2 + 5×4×2$
$=80 + 64 + 40$
$=184$(平方厘米)
11. 把一个正方体木块锯成两个长方体木块,其中小长方体的表面积比大长方体的表面积少20平方厘米。原来正方体木块的棱长是5厘米,小长方体的表面积是多少平方厘米?
答案:11. $(5×5×8 - 20)÷2 = 90$(平方厘米) 提示:把正方体木块锯成两个长方体木块,增加了2个面,两个长方体的表面积之和相当于正方体的8个面的面积和,即$5×5×8 = 200$(平方厘米)。由于小长方体的表面积比大长方体的表面积少20平方厘米,根据和差问题的求法可求出小长方体的表面积。
解析:
正方体一个面的面积:$5×5 = 25$(平方厘米)
两个长方体表面积之和:$6×25 + 2×25 = 8×25 = 200$(平方厘米)
小长方体表面积:$(200 - 20)÷2 = 90$(平方厘米)
答:小长方体的表面积是90平方厘米。
两个长方体表面积之和:$6×25 + 2×25 = 8×25 = 200$(平方厘米)
小长方体表面积:$(200 - 20)÷2 = 90$(平方厘米)
答:小长方体的表面积是90平方厘米。