7. 玲玲要折180颗幸运星,已经折了$\frac {2}{5}$。她再折多少颗幸运星,能使已折颗数与未折颗数的比是$3:1$?
答案:7.$180× \left(\dfrac{3}{3+1}-\dfrac{2}{5}\right)=63$(颗)
8. 粮仓里有100吨大米,第一次运走$\frac {1}{2}$,第二次运走余下的$\frac {1}{3}$,第三次运走余下的$\frac {1}{4}$……最后一次运走余下的$\frac {1}{100}$,这堆大米还剩下多少吨?
答案:8.$\left(1-\dfrac{1}{2}\right)× \left(1-\dfrac{1}{3}\right)× \left(1-\dfrac{1}{4}\right)× \cdots × \left(1-\dfrac{1}{100}\right)=\dfrac{1}{2}× \dfrac{2}{3}× \dfrac{3}{4}× \cdots × \dfrac{99}{100}=\dfrac{1}{100}$ $100× \dfrac{1}{100}=1$(吨) 提示:第一次运走$\dfrac{1}{2}$,剩下原来的$\left(1-\dfrac{1}{2}\right)$,第二次剩下第一次运走后剩下的$\left(1-\dfrac{1}{3}\right)$,则第二次剩下原来的$\left(1-\dfrac{1}{2}\right)× \left(1-\dfrac{1}{3}\right)\cdots \cdots$以此类推,先用乘法求出最后一次剩下原来的几分之几,再求出这堆大米还剩下的质量。
解析:
$\left(1-\dfrac{1}{2}\right)×\left(1-\dfrac{1}{3}\right)×\left(1-\dfrac{1}{4}\right)×\cdots×\left(1-\dfrac{1}{100}\right)$
$=\dfrac{1}{2}×\dfrac{2}{3}×\dfrac{3}{4}×\cdots×\dfrac{99}{100}$
$=\dfrac{1}{100}$
$100×\dfrac{1}{100}=1$(吨)
答:这堆大米还剩下$1$吨。
$=\dfrac{1}{2}×\dfrac{2}{3}×\dfrac{3}{4}×\cdots×\dfrac{99}{100}$
$=\dfrac{1}{100}$
$100×\dfrac{1}{100}=1$(吨)
答:这堆大米还剩下$1$吨。
9. 第一车间有45人,如果从第一车间调9人到第二车间,那么第二车间的人数比第一车间多$\frac {1}{3}$。原来哪个车间人数多?多多少人?
答案:9.原来第二车间人数:$(45-9)× \left(1+\dfrac{1}{3}\right)-9=39$(人) $45-39=6$(人) 原来第一车间人数多,多6人。 提示:第一车间调出9人后,还剩$45-9=36$(人),这时第二车间比第一车间多$\dfrac{1}{3}$,就是说这时第二车间的人数是第一车间的$\left(1+\dfrac{1}{3}\right)$,用$36× \left(1+\dfrac{1}{3}\right)$求出这时第二车间有48人,减去从第一车间调进的9人,得到第二车间原来有39人。比较一下,可知第一车间原来比第二车间多6人。
解析:
第一车间调出9人后人数:$45 - 9 = 36$(人)
此时第二车间人数:$36×\left(1+\dfrac{1}{3}\right)= 36×\dfrac{4}{3}=48$(人)
原来第二车间人数:$48 - 9 = 39$(人)
人数差:$45 - 39 = 6$(人)
原来第一车间人数多,多6人。
此时第二车间人数:$36×\left(1+\dfrac{1}{3}\right)= 36×\dfrac{4}{3}=48$(人)
原来第二车间人数:$48 - 9 = 39$(人)
人数差:$45 - 39 = 6$(人)
原来第一车间人数多,多6人。
10. (1)六(3)班有45人,王老师从男、女生中各选出$\frac {1}{5}$的学生参加书法比赛,剩下的男生有20人,女生有(
(2)六年级有三个班,每班45人,六(1)班男生人数与六(2)班女生人数同样多,六(3)班的$\frac {3}{5}$是男生。六年级女生共有(
(3)六(1)班全班有52名同学,其中男同学占$\frac {7}{13}$,这个班$\frac {3}{4}$的同学参加了“金钥匙”科学竞赛。这个班参加“金钥匙”科学竞赛的男同学至少有(
16
)人没有参加。(2)六年级有三个班,每班45人,六(1)班男生人数与六(2)班女生人数同样多,六(3)班的$\frac {3}{5}$是男生。六年级女生共有(
63
)人。(3)六(1)班全班有52名同学,其中男同学占$\frac {7}{13}$,这个班$\frac {3}{4}$的同学参加了“金钥匙”科学竞赛。这个班参加“金钥匙”科学竞赛的男同学至少有(
15
)人。答案:10.
(1)16 提示:“从男、女生中各选出$\dfrac{1}{5}$的学生参加书法比赛”也就是从全班学生中选出$\dfrac{1}{5}$参加书法比赛,即男生人数$× \dfrac{1}{5}+$女生人数$× \dfrac{1}{5}=$(男生人数+女生人数)$× \dfrac{1}{5}=$全班人数$× \dfrac{1}{5}$。$45× \dfrac{1}{5}=9$(人),$45-9-20=16$(人)。
(2)63 提示:根据“六
(1)班男生人数与六
(2)班女生人数同样多”可知,如果把六
(1)班男生与六
(2)班女生对调,则六
(1)班全部是女生。因为六
(3)班的$\dfrac{3}{5}$是男生,所以六
(3)班女生人数占全班的$\left(1-\dfrac{3}{5}\right)$。用六
(1)班人数加上六
(3)班女生人数,就等于六年级三个班女生的总人数,即$45+45× \left(1-\dfrac{3}{5}\right)=63$(人)。
(3)15 提示:用$52× \dfrac{3}{4}$即可求出参加科学竞赛的人数,也就是39人;男同学占全班人数的$\dfrac{7}{13}$,所以女同学占全班人数的$\left(1-\dfrac{7}{13}\right)$,用$52× \left(1-\dfrac{7}{13}\right)$即可求出这个班女同学的人数,也就是24人,要使参加科学竞赛的男同学人数最少,则女同学全部参加,剩余的人数就是男同学参加的人数,为$39-24=15$(人)。
(1)16 提示:“从男、女生中各选出$\dfrac{1}{5}$的学生参加书法比赛”也就是从全班学生中选出$\dfrac{1}{5}$参加书法比赛,即男生人数$× \dfrac{1}{5}+$女生人数$× \dfrac{1}{5}=$(男生人数+女生人数)$× \dfrac{1}{5}=$全班人数$× \dfrac{1}{5}$。$45× \dfrac{1}{5}=9$(人),$45-9-20=16$(人)。
(2)63 提示:根据“六
(1)班男生人数与六
(2)班女生人数同样多”可知,如果把六
(1)班男生与六
(2)班女生对调,则六
(1)班全部是女生。因为六
(3)班的$\dfrac{3}{5}$是男生,所以六
(3)班女生人数占全班的$\left(1-\dfrac{3}{5}\right)$。用六
(1)班人数加上六
(3)班女生人数,就等于六年级三个班女生的总人数,即$45+45× \left(1-\dfrac{3}{5}\right)=63$(人)。
(3)15 提示:用$52× \dfrac{3}{4}$即可求出参加科学竞赛的人数,也就是39人;男同学占全班人数的$\dfrac{7}{13}$,所以女同学占全班人数的$\left(1-\dfrac{7}{13}\right)$,用$52× \left(1-\dfrac{7}{13}\right)$即可求出这个班女同学的人数,也就是24人,要使参加科学竞赛的男同学人数最少,则女同学全部参加,剩余的人数就是男同学参加的人数,为$39-24=15$(人)。
11. 在六年级96名学生中调查会下中国象棋和国际象棋的人数,发现有24名学生两样都不会,有$\frac {1}{8}$的学生两样都会,有$\frac {7}{12}$的学生会下中国象棋,会下国际象棋的学生有多少名?
答案:
11.$96-24=72$(名) $72-96× \dfrac{7}{12}+96× \dfrac{1}{8}=28$(名) 提示:画图如图所示。先求出会下中国象棋与会下国际象棋的总人数,用这个总人数减去会下中国象棋的人数,求出只会下国际象棋的人数,再加上两样都会的人数,就得到会下国际象棋的总人数。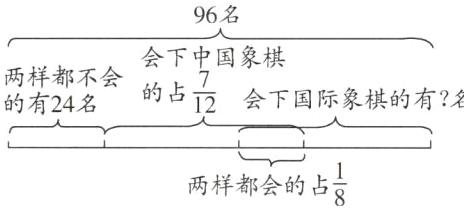
11.$96-24=72$(名) $72-96× \dfrac{7}{12}+96× \dfrac{1}{8}=28$(名) 提示:画图如图所示。先求出会下中国象棋与会下国际象棋的总人数,用这个总人数减去会下中国象棋的人数,求出只会下国际象棋的人数,再加上两样都会的人数,就得到会下国际象棋的总人数。

12. 一个布袋里有红、黄两种颜色的球共140个,拿出红球的$\frac {1}{4}$,再拿出7个黄球,剩下的红球和黄球正好一样多。原来袋中红球、黄球各有多少个?
答案:
12.红球:$(140-7)÷ \left(1-\dfrac{1}{4}+1\right)=76$(个) 黄球:$140-76=64$(个) 提示:如图,根据拿出红球的$\dfrac{1}{4}$,可以把红球的个数看作单位“1”,剩下的红球是红球总数的$\dfrac{3}{4}$。拿出7个黄球后,剩下的数据红球和黄球一样多,就是说剩下的黄球的个数也是红球的$\dfrac{3}{4}$。那么如果只从布袋中拿走7个黄球,剩下的球的总数就是红球的$\left(1+\dfrac{3}{4}\right)$。
12.红球:$(140-7)÷ \left(1-\dfrac{1}{4}+1\right)=76$(个) 黄球:$140-76=64$(个) 提示:如图,根据拿出红球的$\dfrac{1}{4}$,可以把红球的个数看作单位“1”,剩下的红球是红球总数的$\dfrac{3}{4}$。拿出7个黄球后,剩下的数据红球和黄球一样多,就是说剩下的黄球的个数也是红球的$\dfrac{3}{4}$。那么如果只从布袋中拿走7个黄球,剩下的球的总数就是红球的$\left(1+\dfrac{3}{4}\right)$。

13. 假设思想 校游泳队原有队员120人,今年女队员增加了$\frac {1}{8}$,男队员减少了$\frac {1}{6}$,现在有队员114人。原来男、女队员分别有多少人?
答案:13.$120× \left(1-\dfrac{1}{6}\right)=100$(人) 女队员:$(114-100)÷ \left(\dfrac{1}{8}+\dfrac{1}{6}\right)=48$(人) 男队员:$120-48=72$(人) 提示:队员的人数变化是女队员增加,男队员减少,我们可以假设两组队员同时增加或同时减少相同的分率,来充分利用总数这个已知条件,假设男、女队员都减少了$\dfrac{1}{6}$,这时总人数是$120× \left(1-\dfrac{1}{6}\right)=100$(人)。再把这个条件与已知条件比较,相差的人数是因为女队员增加了$\dfrac{1}{8}$变成了减少$\dfrac{1}{6}$,因此$(114-100)$人对应的分率是女队员的$\left(\dfrac{1}{8}+\dfrac{1}{6}\right)$,这样就可以求出原来女队员的人数是$(114-100)÷ \left(\dfrac{1}{8}+\dfrac{1}{6}\right)=48$(人),则原来男队员的人数是$120-48=72$(人)。
解析:
假设男、女队员都减少了$\frac{1}{6}$,此时总人数为:$120×\left(1 - \frac{1}{6}\right)=100$(人)
女队员人数:$(114 - 100)÷\left(\frac{1}{8}+\frac{1}{6}\right)=48$(人)
男队员人数:$120 - 48 = 72$(人)
答:原来男队员有72人,女队员有48人。
女队员人数:$(114 - 100)÷\left(\frac{1}{8}+\frac{1}{6}\right)=48$(人)
男队员人数:$120 - 48 = 72$(人)
答:原来男队员有72人,女队员有48人。