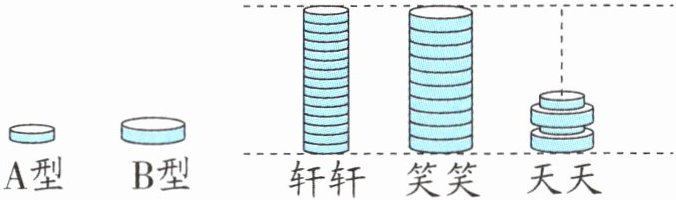
2. 如图,轩轩用 15 块 A 型积木搭,笑笑用 10 块 B 型积木搭,两人搭的高度相同。天天用一块 A 型积木和一块 B 型积木间隔地搭,如果搭的高度与轩轩和笑笑的相同,那么天天用 A 型积木和 B 型积木各多少块?

答案:$1÷ \left(\frac{1}{15}+\frac{1}{10}\right)=6$(块) 用A型积木和B型积木各6块
解析:
设搭的高度为单位“1”,则A型积木的高度为$\frac{1}{15}$,B型积木的高度为$\frac{1}{10}$。
$1÷ \left(\frac{1}{15}+\frac{1}{10}\right)$
$=1÷ \left(\frac{2}{30}+\frac{3}{30}\right)$
$=1÷ \frac{5}{30}$
$=1× 6$
$=6$(块)
用A型积木和B型积木各6块。
$1÷ \left(\frac{1}{15}+\frac{1}{10}\right)$
$=1÷ \left(\frac{2}{30}+\frac{3}{30}\right)$
$=1÷ \frac{5}{30}$
$=1× 6$
$=6$(块)
用A型积木和B型积木各6块。
3. “冬季两项”是传统冰雪项目,它是将越野滑雪和射击相结合的运动。男子个人比赛的全长是 20 千米,每滑行全长的$\frac {1}{5}$就停下射击 1 次。如图,当一个运动员在比赛中完成第 3 次射击时,他还要滑行多少千米才能到达终点?


答案:$1-\frac{3}{5}=\frac{2}{5}$ $20× \frac{2}{5}=8$(千米)
解析:
$1-\frac{3}{5}=\frac{2}{5}$
$20×\frac{2}{5}=8$(千米)
答:他还要滑行8千米才能到达终点。
$20×\frac{2}{5}=8$(千米)
答:他还要滑行8千米才能到达终点。
4. 某车间原计划制造一种零件,每个需用钢材$\frac {3}{4}$千克,改进设计后,每个零件所用的钢材比原来节约$\frac {1}{6}$。照这样计算,现在做 400 个这样的零件需要钢材多少千克?
答案:$\frac{3}{4}× \left(1-\frac{1}{6}\right)× 400=250$(千克)
解析:
$\frac{3}{4} × \left(1 - \frac{1}{6}\right) × 400$
$=\frac{3}{4} × \frac{5}{6} × 400$
$=\frac{5}{8} × 400$
$=250$(千克)
答:现在做 400 个这样的零件需要钢材 250 千克。
$=\frac{3}{4} × \frac{5}{6} × 400$
$=\frac{5}{8} × 400$
$=250$(千克)
答:现在做 400 个这样的零件需要钢材 250 千克。
5. 一本 240 页的故事书,第一天看的页数与总页数的比是 1:5,第二天再看多少页,还剩下这本书的$\frac {2}{3}$没看?
答案:$240× \left(1-\frac{1}{5}-\frac{2}{3}\right)=32$(页)
6. 王老师下载一部影片,前 10 秒下载了 256 MB,之后加入会员,速度提高了$\frac {1}{2}$,又用了 60 秒将电影全部下载完。这部电影一共有多少 GB?(1 GB = 1024 MB)
答案:$256÷ 10× \left(1+\frac{1}{2}\right)× 60+256=2560$(MB) $2560÷ 1024=2.5$(GB) 提示:速度提高了$\frac{1}{2}$,则现在每秒下载$256÷ 10× \left(1+\frac{1}{2}\right)=38.4$(MB),后60秒下载了$38.4× 60=2304$(MB),所以这部电影一共有$2304+256=2560$(MB),最后注意转化单位即可。
解析:
$256÷10×\left(1+\frac{1}{2}\right)×60+256=2560$(MB)
$2560÷1024=2.5$(GB)
答:这部电影一共有$2.5$GB。
$2560÷1024=2.5$(GB)
答:这部电影一共有$2.5$GB。
7. 六年级会围棋的比不会围棋的人数少 16 人。经过一段时间的学习,不会围棋的人数中有$\frac {1}{8}$的人学会了围棋,此时会围棋的和不会围棋的人数一样多,六年级共有多少人?
答案:$16÷ \left(\frac{1}{8}× 2\right)=64$(人) $64× \left(1-\frac{1}{8}× 2\right)=48$(人) $64+48=112$(人) 提示:根据题意,把不会围棋的人数看作单位“1”,会围棋的比不会围棋的人数少16人,经过一段时间的学习,不会围棋 的人数中有$\frac{1}{8}$的人学会了围棋,此时会围棋的和不会围棋的人数一样多,那么会围棋的比不会围棋的人数少的16人就相当于不会围棋的人数的$\frac{1}{8}× 2$,所以不会围棋的人数是$16÷ \left(\frac{1}{8}× 2\right)=64$(人),会围棋的人数是$64× \left(1-\frac{1}{8}× 2\right)=48$(人),六年级共有$64+48=112$(人)。
解析:
不会围棋的人数:$16÷\left(\frac{1}{8}×2\right)=64$(人)
会围棋的人数:$64×\left(1 - \frac{1}{8}×2\right)=48$(人)
六年级总人数:$64 + 48 = 112$(人)
答:六年级共有112人。
会围棋的人数:$64×\left(1 - \frac{1}{8}×2\right)=48$(人)
六年级总人数:$64 + 48 = 112$(人)
答:六年级共有112人。
强基直通车 一项工程,甲队单独做 12 天可以完成,若甲队单独做 3 天后乙队接着单独做 2 天,则正好完成全部工作量的一半。现在甲、乙两队合做若干天后,由乙队单独完成,做完后发现两段所用的时间相等,则完成全部工作量一共用了多少天?
答案:乙队的工作效率:$\left(\frac{1}{2}-\frac{1}{12}× \right. 3\left. \right)÷ 2=\frac{1}{8}$ 设甲、乙两队合做了x天。根据题意,得$\left(\frac{1}{12}+\frac{1}{8}\right)x+\frac{1}{8}x=1$ $x=3$ $3+3=6$(天) 提示:把工作总量看作单位“1”,根据“工作总量÷工作时间=工作效率”求出甲队的工作效率,进而求出甲队单独做3天完成的工作量,用“$\frac{1}{2}-$甲队单独做3天完成的工作量”求出乙队完成的工作量,根据“工作总量÷工作时间=工作效率”计算出乙队的工作效率,即$\left(\frac{1}{2}-\frac{1}{12}× 3\right)÷ 2=\frac{1}{8}$;根据两段时间相等,设甲、乙两队合做了x天,进而列出方程$\left(\frac{1}{12}+\frac{1}{8}\right)x+\frac{1}{8}x=1$,进行解答即可。
解析:
乙队的工作效率:$\left(\frac{1}{2}-\frac{1}{12}×3\right)÷2=\frac{1}{8}$
设甲、乙两队合做了$x$天。
$\left(\frac{1}{12}+\frac{1}{8}\right)x+\frac{1}{8}x=1$
$\frac{5}{24}x+\frac{3}{24}x=1$
$\frac{8}{24}x=1$
$x=3$
$3+3=6$(天)
答:完成全部工作量一共用了$6$天。
设甲、乙两队合做了$x$天。
$\left(\frac{1}{12}+\frac{1}{8}\right)x+\frac{1}{8}x=1$
$\frac{5}{24}x+\frac{3}{24}x=1$
$\frac{8}{24}x=1$
$x=3$
$3+3=6$(天)
答:完成全部工作量一共用了$6$天。