3. 有一道题目：纸箱内原本有 10 千克苹果,____,还剩多少千克？如果列式为$(10-\frac {4}{5})×(1-\frac {4}{5})$,那么横线上的条件是(
A.第一次吃了$\frac {4}{5}$千克,第二次吃了$\frac {4}{5}$千克
B.第一次吃了$\frac {4}{5}$
C.第一次吃了$\frac {4}{5}$,第二次吃了$\frac {4}{5}$千克
D.第一次吃了$\frac {4}{5}$,第二次吃了剩下的$\frac {4}{5}$
B
)。A.第一次吃了$\frac {4}{5}$千克,第二次吃了$\frac {4}{5}$千克
B.第一次吃了$\frac {4}{5}$
千
克,第二次吃了剩下的$\frac {4}{5}$C.第一次吃了$\frac {4}{5}$,第二次吃了$\frac {4}{5}$千克
D.第一次吃了$\frac {4}{5}$,第二次吃了剩下的$\frac {4}{5}$
答案：B
解析：
$(10-\frac{4}{5})$表示第一次吃了$\frac{4}{5}$千克后剩下的苹果质量，$(1-\frac{4}{5})$表示第二次吃了剩下的$\frac{4}{5}$后剩余的比例，所以横线上的条件是第一次吃了$\frac{4}{5}$千克，第二次吃了剩下的$\frac{4}{5}$。
B
B
4. 一根绳子,剪去$\frac {1}{8}$后,又接上$\frac {1}{8}$米,现在绳子变长了,则原来这根绳子(
A.比 1 米长
B.比 1 米短
C.正好是 1 米
D.无法确定
B
)。A.比 1 米长
B.比 1 米短
C.正好是 1 米
D.无法确定
答案：B
解析：
设原来绳子长为$x$米。
剪去$\frac{1}{8}$后长度为$x - \frac{1}{8}x=\frac{7}{8}x$米，接上$\frac{1}{8}$米后长度为$\frac{7}{8}x+\frac{1}{8}$米。
因为现在绳子变长，所以$\frac{7}{8}x+\frac{1}{8} ＞ x$，
$\frac{7}{8}x+\frac{1}{8} ＞ x$
$\frac{1}{8} ＞ x-\frac{7}{8}x$
$\frac{1}{8} ＞ \frac{1}{8}x$
$x ＜ 1$
B
剪去$\frac{1}{8}$后长度为$x - \frac{1}{8}x=\frac{7}{8}x$米，接上$\frac{1}{8}$米后长度为$\frac{7}{8}x+\frac{1}{8}$米。
因为现在绳子变长，所以$\frac{7}{8}x+\frac{1}{8} ＞ x$，
$\frac{7}{8}x+\frac{1}{8} ＞ x$
$\frac{1}{8} ＞ x-\frac{7}{8}x$
$\frac{1}{8} ＞ \frac{1}{8}x$
$x ＜ 1$
B
5. 甲筐橘子比乙筐橘子多 20 千克,如果两筐都卖掉$\frac {1}{5}$,现在这两筐橘子相差(
A.4
B.16
C.32
D.40
B
)千克。A.4
B.16
C.32
D.40
答案：B
解析：
设乙筐橘子重$x$千克，则甲筐橘子重$(x + 20)$千克。
两筐都卖掉$\frac{1}{5}$后，
甲筐剩余：$(x + 20)×(1 - \frac{1}{5})=(x + 20)×\frac{4}{5}=\frac{4}{5}x + 16$
乙筐剩余：$x×(1 - \frac{1}{5})=\frac{4}{5}x$
两筐相差：$(\frac{4}{5}x + 16)-\frac{4}{5}x = 16$
B
两筐都卖掉$\frac{1}{5}$后，
甲筐剩余：$(x + 20)×(1 - \frac{1}{5})=(x + 20)×\frac{4}{5}=\frac{4}{5}x + 16$
乙筐剩余：$x×(1 - \frac{1}{5})=\frac{4}{5}x$
两筐相差：$(\frac{4}{5}x + 16)-\frac{4}{5}x = 16$
B
6. 小红在计算$(a+\frac {5}{9})×3$时,错误地算成了$a+\frac {5}{9}×3$,她计算的结果与正确结果相差(
A.$\frac {1}{2}a$
B.$\frac {1}{3}a$
C.2a
D.3a
C
)。A.$\frac {1}{2}a$
B.$\frac {1}{3}a$
C.2a
D.3a
答案：C 提示:根据乘法分配律,$\left(a+\frac{5}{9}\right)× 3=3a+\frac{5}{9}× 3$,与错误的算式$a+\frac{5}{9}× 3$对比发现,她计算的结果与正确结果相差$3a-a=2a$。
7. 足球和篮球共 75 个,把足球的$\frac {2}{5}$换成篮球,结果足球和篮球的个数比是 1:4。原来有(
A.20
B.30
C.35
D.25
25
)个足球。A.20
B.30
C.35
D.25
答案：D 提示:足球和篮球的总数不变,一直都是75个,当足球和篮球的个数比是$1:4$时,足球有$75× \frac{1}{1+4}=15$(个),原来足球有$15÷ \left(1-\frac{2}{5}\right)=25$(个)。
四、计算题。(怎样算简便就怎样算)
$4×(\frac {1}{9}-\frac {1}{12})×9$ $\frac {3}{7}×\frac {4}{11}+\frac {7}{11}÷\frac {7}{3}$
$4×(\frac {1}{9}-\frac {1}{12})×9$ $\frac {3}{7}×\frac {4}{11}+\frac {7}{11}÷\frac {7}{3}$
答案：1$\frac{3}{7}$ 8$\frac{8}{9}$
解析：
$4×(\frac{1}{9}-\frac{1}{12})×9$
$=4×9×(\frac{1}{9}-\frac{1}{12})$
$=36×\frac{1}{9}-36×\frac{1}{12}$
$=4 - 3$
$=1$
$\frac{3}{7}×\frac{4}{11}+\frac{7}{11}÷\frac{7}{3}$
$=\frac{3}{7}×\frac{4}{11}+\frac{7}{11}×\frac{3}{7}$
$=\frac{3}{7}×(\frac{4}{11}+\frac{7}{11})$
$=\frac{3}{7}×1$
$=\frac{3}{7}$
$=4×9×(\frac{1}{9}-\frac{1}{12})$
$=36×\frac{1}{9}-36×\frac{1}{12}$
$=4 - 3$
$=1$
$\frac{3}{7}×\frac{4}{11}+\frac{7}{11}÷\frac{7}{3}$
$=\frac{3}{7}×\frac{4}{11}+\frac{7}{11}×\frac{3}{7}$
$=\frac{3}{7}×(\frac{4}{11}+\frac{7}{11})$
$=\frac{3}{7}×1$
$=\frac{3}{7}$
$7÷\frac {7}{9}-\frac {7}{9}÷7$ $\frac {3}{8}÷5+\frac {1}{8}×\frac {2}{5}$
答案：$\frac{1}{8}$ 6
解析：
$7÷\frac{7}{9}-\frac{7}{9}÷7$
$=7×\frac{9}{7}-\frac{7}{9}×\frac{1}{7}$
$=9-\frac{1}{9}$
$=8\frac{8}{9}$
$\frac{3}{8}÷5+\frac{1}{8}×\frac{2}{5}$
$=\frac{3}{8}×\frac{1}{5}+\frac{1}{8}×\frac{2}{5}$
$=\frac{3}{40}+\frac{2}{40}$
$=\frac{5}{40}$
$=\frac{1}{8}$
1
$=7×\frac{9}{7}-\frac{7}{9}×\frac{1}{7}$
$=9-\frac{1}{9}$
$=8\frac{8}{9}$
$\frac{3}{8}÷5+\frac{1}{8}×\frac{2}{5}$
$=\frac{3}{8}×\frac{1}{5}+\frac{1}{8}×\frac{2}{5}$
$=\frac{3}{40}+\frac{2}{40}$
$=\frac{5}{40}$
$=\frac{1}{8}$
1
$\frac {1}{17}+(\frac {5}{8}+\frac {2}{17})×8$ $(\frac {8}{11}+\frac {8}{13})÷(\frac {3}{11}+\frac {3}{13})$
答案：$\frac{8}{3}$ $\frac{8}{17}$
解析：
第一题：$\frac{1}{17}+(\frac{5}{8}+\frac{2}{17})×8$
$\begin{aligned}&\frac{1}{17}+(\frac{5}{8}+\frac{2}{17})×8\\=&\frac{1}{17}+\frac{5}{8}×8+\frac{2}{17}×8\\=&\frac{1}{17}+5+\frac{16}{17}\\=&5+(\frac{1}{17}+\frac{16}{17})\\=&5+1\\=&6\end{aligned}$
第二题：$(\frac{8}{11}+\frac{8}{13})÷(\frac{3}{11}+\frac{3}{13})$
$\begin{aligned}&(\frac{8}{11}+\frac{8}{13})÷(\frac{3}{11}+\frac{3}{13})\\=&8×(\frac{1}{11}+\frac{13}{13})÷[3×(\frac{1}{11}+\frac{1}{13})]\\=&\frac{8}{3}\end{aligned}$
1
$\begin{aligned}&\frac{1}{17}+(\frac{5}{8}+\frac{2}{17})×8\\=&\frac{1}{17}+\frac{5}{8}×8+\frac{2}{17}×8\\=&\frac{1}{17}+5+\frac{16}{17}\\=&5+(\frac{1}{17}+\frac{16}{17})\\=&5+1\\=&6\end{aligned}$
第二题：$(\frac{8}{11}+\frac{8}{13})÷(\frac{3}{11}+\frac{3}{13})$
$\begin{aligned}&(\frac{8}{11}+\frac{8}{13})÷(\frac{3}{11}+\frac{3}{13})\\=&8×(\frac{1}{11}+\frac{13}{13})÷[3×(\frac{1}{11}+\frac{1}{13})]\\=&\frac{8}{3}\end{aligned}$
1
$\frac {8}{11}×[\frac {9}{5}-(\frac {4}{5}+\frac {6}{17})]$ $166\frac {1}{20}÷41$
答案：$\frac{8}{17}$ 4$\frac{1}{20}$
解析：
$\frac{8}{11}×[\frac{9}{5}-(\frac{4}{5}+\frac{6}{17})]$
$=\frac{8}{11}×[\frac{9}{5}-\frac{4}{5}-\frac{6}{17}]$
$=\frac{8}{11}×[1-\frac{6}{17}]$
$=\frac{8}{11}×\frac{11}{17}$
$=\frac{8}{17}$
$166\frac{1}{20}÷41$
$=(164 + 2\frac{1}{20})÷41$
$=164÷41 + \frac{41}{20}÷41$
$=4 + \frac{1}{20}$
$=4\frac{1}{20}$
$=\frac{8}{11}×[\frac{9}{5}-\frac{4}{5}-\frac{6}{17}]$
$=\frac{8}{11}×[1-\frac{6}{17}]$
$=\frac{8}{11}×\frac{11}{17}$
$=\frac{8}{17}$
$166\frac{1}{20}÷41$
$=(164 + 2\frac{1}{20})÷41$
$=164÷41 + \frac{41}{20}÷41$
$=4 + \frac{1}{20}$
$=4\frac{1}{20}$
五、操作题。
画一个面积是 18 平方厘米的长方形,使它的长和宽的比是 2:1。(每个小方格的边长都是 1 厘米)
如果长方形的长增加$\frac {1}{3}$,宽减少$\frac {1}{5}$,得到的长方形的面积是原来的( )；如果长方形的长减少$\frac {1}{9}$,要使面积不变,宽应该( )(填“增加”或“减少”)( )。
画一个面积是 18 平方厘米的长方形,使它的长和宽的比是 2:1。(每个小方格的边长都是 1 厘米)
如果长方形的长增加$\frac {1}{3}$,宽减少$\frac {1}{5}$,得到的长方形的面积是原来的( )；如果长方形的长减少$\frac {1}{9}$,要使面积不变,宽应该( )(填“增加”或“减少”)( )。
答案：
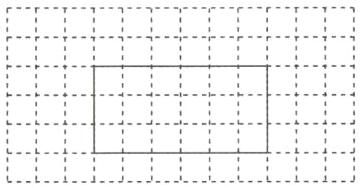(合理即可) $\frac{16}{15}$ 增加 $\frac{1}{8}$
(合理即可) $\frac{16}{15}$ 增加 $\frac{1}{8}$1. 玩具厂的一车间有 120 人,二车间的人数比一车间多$\frac {1}{6}$,三车间的人数比二车间少$\frac {1}{7}$。
(1)二车间有(
(2)三车间再增加多少人就比一车间多$\frac {1}{8}$？
(1)二车间有(
140
)人,三车间有(120
)人。(2)三车间再增加多少人就比一车间多$\frac {1}{8}$？
$120× \left(1+\frac{1}{8}\right)=135$(人) $135-120=15$(人)
答案：
(1)140 120
(2)$120× \left(1+\frac{1}{8}\right)=135$(人) $135-120=15$(人)
(1)140 120
(2)$120× \left(1+\frac{1}{8}\right)=135$(人) $135-120=15$(人)