1. (
144
)米比 120 米多$\frac {1}{5}$,72 千克减少$\frac {1}{4}$千克是(71$\frac{3}{4}$
)千克。答案:144 71$\frac{3}{4}$
2. 平角的$\frac {1}{3}$比周角的$\frac {1}{5}$少
12
度。答案:12
解析:
周角为$360^\circ$,其$\frac{1}{5}$为$360^\circ×\frac{1}{5} = 72^\circ$;平角为$180^\circ$,其$\frac{1}{3}$为$180^\circ×\frac{1}{3} = 60^\circ$;$72^\circ - 60^\circ = 12^\circ$。
12
12
3. $[(\frac {5}{14}-□)÷\frac {3}{10}]×\frac {14}{15}= \frac {2}{3}$,$□=$(
$\frac{1}{7}$
)。答案:$\frac{1}{7}$
解析:
设$□=x$,则$[(\frac{5}{14}-x)÷\frac{3}{10}]×\frac{14}{15}=\frac{2}{3}$
$(\frac{5}{14}-x)÷\frac{3}{10}=\frac{2}{3}÷\frac{14}{15}$
$(\frac{5}{14}-x)÷\frac{3}{10}=\frac{5}{7}$
$\frac{5}{14}-x=\frac{5}{7}×\frac{3}{10}$
$\frac{5}{14}-x=\frac{3}{14}$
$x=\frac{5}{14}-\frac{3}{14}$
$x=\frac{1}{7}$
$\frac{1}{7}$
$(\frac{5}{14}-x)÷\frac{3}{10}=\frac{2}{3}÷\frac{14}{15}$
$(\frac{5}{14}-x)÷\frac{3}{10}=\frac{5}{7}$
$\frac{5}{14}-x=\frac{5}{7}×\frac{3}{10}$
$\frac{5}{14}-x=\frac{3}{14}$
$x=\frac{5}{14}-\frac{3}{14}$
$x=\frac{1}{7}$
$\frac{1}{7}$
4. $m×n= \frac {1}{200}$,$(m×100)×(n÷20)= $
$\frac{1}{40}$
;$m+n= 150$,$m×\frac {3}{5}+n×\frac {3}{5}= $90
。答案:$\frac{1}{40}$ 90
解析:
$(m×100)×(n÷20)=m×n×100÷20=\frac{1}{200}×5=\frac{1}{40}$;$m×\frac{3}{5}+n×\frac{3}{5}=(m+n)×\frac{3}{5}=150×\frac{3}{5}=90$
5. 甲仓库有 60 吨货物,乙仓库比甲仓库多$\frac {1}{5}$,丙仓库比甲仓库少$\frac {1}{5}$吨,乙仓库有货物(
72
)吨,丙仓库有货物(59$\frac{4}{5}$
)吨。答案:72 59$\frac{4}{5}$
解析:
乙仓库:$60 + 60×\frac{1}{5} = 60 + 12 = 72$(吨)
丙仓库:$60 - \frac{1}{5} = 59\frac{4}{5}$(吨)
72 $59\frac{4}{5}$
丙仓库:$60 - \frac{1}{5} = 59\frac{4}{5}$(吨)
72 $59\frac{4}{5}$
6. 心缘服饰公司计划十月份制作西服 800 套,结果上半月完成了计划的$\frac {3}{5}$,下半月完成了计划的$\frac {5}{8}$。十月份超额制作(
180
)套西服。答案:180
解析:
$800×\left(\frac{3}{5}+\frac{5}{8}-1\right)$
$=800×\left(\frac{24}{40}+\frac{25}{40}-\frac{40}{40}\right)$
$=800×\frac{9}{40}$
$=180$
180
$=800×\left(\frac{24}{40}+\frac{25}{40}-\frac{40}{40}\right)$
$=800×\frac{9}{40}$
$=180$
180
7. 服装厂第一车间有 150 人,其中第一组的人数是第一车间总人数的$\frac {2}{5}$,余下人数的$\frac {4}{9}$正好与第二组的人数相等。第二组有(
40
)人。答案:40
解析:
150×(1-$\frac{2}{5}$)=90(人)
90×$\frac{4}{9}$=40(人)
40
90×$\frac{4}{9}$=40(人)
40
8. 从甲地到乙地,$\frac {2}{5}$是上坡路,$\frac {1}{4}$是平路,$\frac {7}{20}$是下坡路,一辆汽车从甲地开往乙地,又从乙地返回甲地,共走了 60 千米的上坡路。甲、乙两地相距(
80
)千米。答案:80
解析:
设甲、乙两地相距$x$千米。
从甲地到乙地,上坡路为$\frac{2}{5}x$千米,下坡路为$\frac{7}{20}x$千米;从乙地返回甲地,上坡路为$\frac{7}{20}x$千米,下坡路为$\frac{2}{5}x$千米。
往返共走的上坡路为:$\frac{2}{5}x+\frac{7}{20}x$
$\begin{aligned}\frac{2}{5}x+\frac{7}{20}x&=\frac{8}{20}x+\frac{7}{20}x\\&=\frac{15}{20}x\\&=\frac{3}{4}x\end{aligned}$
已知往返共走了$60$千米上坡路,可得$\frac{3}{4}x = 60$,解得$x=60÷\frac{3}{4}=60×\frac{4}{3}=80$。
80
从甲地到乙地,上坡路为$\frac{2}{5}x$千米,下坡路为$\frac{7}{20}x$千米;从乙地返回甲地,上坡路为$\frac{7}{20}x$千米,下坡路为$\frac{2}{5}x$千米。
往返共走的上坡路为:$\frac{2}{5}x+\frac{7}{20}x$
$\begin{aligned}\frac{2}{5}x+\frac{7}{20}x&=\frac{8}{20}x+\frac{7}{20}x\\&=\frac{15}{20}x\\&=\frac{3}{4}x\end{aligned}$
已知往返共走了$60$千米上坡路,可得$\frac{3}{4}x = 60$,解得$x=60÷\frac{3}{4}=60×\frac{4}{3}=80$。
80
9. 如图,平行四边形的面积是 60 平方米,甲的面积占总面积的$\frac {1}{3}$,乙的面积是(
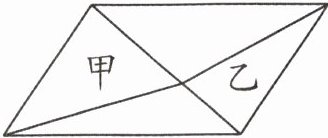
10
)平方米。
答案:10
10. 乐乐书桌上的小书架上的书在 40~50 本之间,其中科普书占$\frac {1}{6}$,故事书占$\frac {3}{8}$,其余的是教辅书。教辅书有(
22
)本。答案:22 提示:书的本数是整数,根据科普书和故事书占总本数的情况,可以判断书的总本数是6和8的公倍数,再根据书的总本数在40~50之间,可以确定一共有48本书。再用$48× \left(1-\frac{1}{6}-\frac{3}{8}\right)$算出教辅书有22本。
解析:
书的总本数是6和8的公倍数,6和8的最小公倍数是24,在40~50之间的公倍数是48。
教辅书数量为:$48×\left(1 - \frac{1}{6} - \frac{3}{8}\right) = 48×\left(\frac{24}{24} - \frac{4}{24} - \frac{9}{24}\right) = 48×\frac{11}{24} = 22$
22
教辅书数量为:$48×\left(1 - \frac{1}{6} - \frac{3}{8}\right) = 48×\left(\frac{24}{24} - \frac{4}{24} - \frac{9}{24}\right) = 48×\frac{11}{24} = 22$
22
11. 林凡、陈帆在银行共存款 9600 元,如果两人分别取出自己存款的$\frac {2}{5}$,再从林凡的存款中取 120 元给陈帆存上,这时两人的存款钱数相等,陈帆原来的存款有(
4600
)元。答案:4600 提示:“如果两人分别取出自己存款的$\frac{2}{5}$”也就是两人一共取出总存款的$\frac{2}{5}$,即林凡的存款$× \frac{2}{5}+$陈帆的存款$× \frac{2}{5}=$(林凡的存款+陈帆的存款)$× \frac{2}{5}=$总存款$× \frac{2}{5}$。两人最后的存款钱数都是$9600× \left(1-\frac{2}{5}\right)÷ 2=2880$(元),所以陈帆原来的存款钱数$=(2880-120)÷ \left(1-\frac{2}{5}\right)=4600$(元)。
解析:
两人取出存款的$\frac{2}{5}$后,剩余总存款为:$9600×\left(1 - \frac{2}{5}\right)=9600×\frac{3}{5}=5760$(元)
此时两人存款相等,各有:$5760÷2 = 2880$(元)
陈帆在得到120元前的存款为:$2880 - 120=2760$(元)
陈帆原来的存款为:$2760÷\left(1 - \frac{2}{5}\right)=2760÷\frac{3}{5}=2760×\frac{5}{3}=4600$(元)
4600
此时两人存款相等,各有:$5760÷2 = 2880$(元)
陈帆在得到120元前的存款为:$2880 - 120=2760$(元)
陈帆原来的存款为:$2760÷\left(1 - \frac{2}{5}\right)=2760÷\frac{3}{5}=2760×\frac{5}{3}=4600$(元)
4600
二、判断题。
1. $\frac {4}{9}÷\frac {4}{5}+\frac {4}{9}÷\frac {1}{5}= \frac {4}{9}÷(\frac {4}{5}+\frac {1}{5})= \frac {4}{9}÷1= \frac {4}{9}$(
2. 一堆煤,烧去$\frac {1}{10}$后,又运来剩下煤的$\frac {1}{10}$,现在的煤与原来同样多。(
3. 一根绳子长$\frac {2}{7}$米,用去$\frac {1}{7}$,还剩$\frac {1}{7}$米。(
4. 男生比女生多$\frac {1}{4}$,则女生比男生少$\frac {1}{4}$。(
1. $\frac {4}{9}÷\frac {4}{5}+\frac {4}{9}÷\frac {1}{5}= \frac {4}{9}÷(\frac {4}{5}+\frac {1}{5})= \frac {4}{9}÷1= \frac {4}{9}$(
×
)2. 一堆煤,烧去$\frac {1}{10}$后,又运来剩下煤的$\frac {1}{10}$,现在的煤与原来同样多。(
×
)3. 一根绳子长$\frac {2}{7}$米,用去$\frac {1}{7}$,还剩$\frac {1}{7}$米。(
×
)4. 男生比女生多$\frac {1}{4}$,则女生比男生少$\frac {1}{4}$。(
×
)答案:1. × 2. × 3. × 4. ×
1. 甲数是 m,比乙数的$\frac {3}{5}$多 n,表示乙数的式子是(
A.$m×\frac {3}{5}+n$
B.$m÷\frac {3}{5}-n$
C.$(m-n)÷\frac {3}{5}$
D.$(m+n)÷\frac {3}{5}$
C
)。A.$m×\frac {3}{5}+n$
B.$m÷\frac {3}{5}-n$
C.$(m-n)÷\frac {3}{5}$
D.$(m+n)÷\frac {3}{5}$
答案:C
解析:
设乙数为$x$。
由题意得:$\frac{3}{5}x + n = m$
$\frac{3}{5}x = m - n$
$x = (m - n) ÷ \frac{3}{5}$
C
由题意得:$\frac{3}{5}x + n = m$
$\frac{3}{5}x = m - n$
$x = (m - n) ÷ \frac{3}{5}$
C
2. 算式$\frac {2}{9}+\frac {a}{9}×\frac {b}{7}(\frac {a}{9}和\frac {b}{7}$都是真分数)的计算结果(
A.小于 1
B.等于 1
C.大于 1
D.无法确定
A
)。A.小于 1
B.等于 1
C.大于 1
D.无法确定
答案:A
解析:
因为$\frac{a}{9}$和$\frac{b}{7}$都是真分数,所以$a < 9$,$b < 7$,则$\frac{a}{9} < 1$,$\frac{b}{7} < 1$,所以$\frac{a}{9}×\frac{b}{7} < 1×1 = 1$,又因为$\frac{a}{9}×\frac{b}{7} > 0$,所以$\frac{2}{9}+\frac{a}{9}×\frac{b}{7} < \frac{2}{9}+1 = \frac{11}{9}$,且$\frac{2}{9}+\frac{a}{9}×\frac{b}{7} > \frac{2}{9}$。
当$a$、$b$取最大值时,$a = 8$,$b = 6$,则$\frac{a}{9}×\frac{b}{7}=\frac{8}{9}×\frac{6}{7}=\frac{48}{63}=\frac{16}{21}$,$\frac{2}{9}+\frac{16}{21}=\frac{14}{63}+\frac{48}{63}=\frac{62}{63} < 1$。
综上,算式的计算结果小于 1。
A
当$a$、$b$取最大值时,$a = 8$,$b = 6$,则$\frac{a}{9}×\frac{b}{7}=\frac{8}{9}×\frac{6}{7}=\frac{48}{63}=\frac{16}{21}$,$\frac{2}{9}+\frac{16}{21}=\frac{14}{63}+\frac{48}{63}=\frac{62}{63} < 1$。
综上,算式的计算结果小于 1。
A