1. 牧羊人正在放牧,一个人牵着一只羊问他:“你有多少只羊?”牧羊人答道:“这群羊加上一倍,再加上原来羊群的一半,又加上原来羊群的四分之一,算上你牵来的羊,正好满一百只.”牧羊人有羊(
A.32只
B.34只
C.36只
D.38只
C
)A.32只
B.34只
C.36只
D.38只
答案:C
解析:
解:设牧羊人有羊$x$只。
根据题意可列方程:$x + x + \frac{1}{2}x + \frac{1}{4}x + 1 = 100$
合并同类项得:$(1 + 1 + \frac{1}{2} + \frac{1}{4})x + 1 = 100$
计算括号内:$\frac{4}{4} + \frac{4}{4} + \frac{2}{4} + \frac{1}{4} = \frac{11}{4}$,即$\frac{11}{4}x + 1 = 100$
移项得:$\frac{11}{4}x = 99$
解得:$x = 99 × \frac{4}{11} = 36$
答案:C
根据题意可列方程:$x + x + \frac{1}{2}x + \frac{1}{4}x + 1 = 100$
合并同类项得:$(1 + 1 + \frac{1}{2} + \frac{1}{4})x + 1 = 100$
计算括号内:$\frac{4}{4} + \frac{4}{4} + \frac{2}{4} + \frac{1}{4} = \frac{11}{4}$,即$\frac{11}{4}x + 1 = 100$
移项得:$\frac{11}{4}x = 99$
解得:$x = 99 × \frac{4}{11} = 36$
答案:C
2. 七年级某班的一个综合实践活动小组去A,B两家超市调查去年和今年“春节”期间的销售情况,如图是调查后小敏与其他两名同学进行交流的情景.根据他们的对话,请分别求出A,B两家超市今年“春节”期间的销售额.
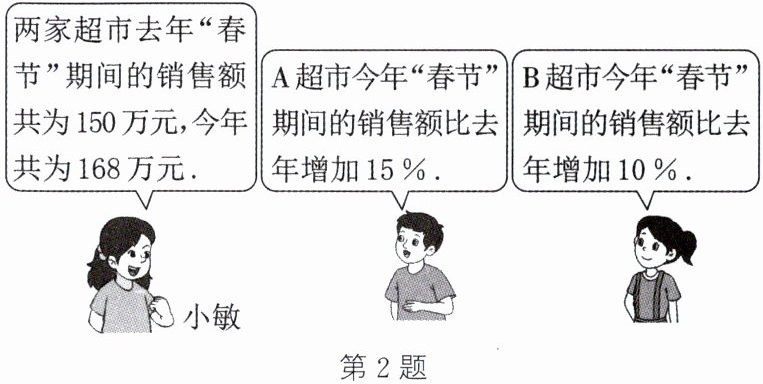

答案:解:设A超市去年“春节”期间的销售额为$x$万元,则B超市去年“春节”期间的销售额为$(150 - x)$万元。
根据题意,得:
$(1 + 15\%)x + (1 + 10\%)(150 - x) = 168$
解得:$x = 60$
则B超市去年销售额为:$150 - 60 = 90$(万元)
A超市今年销售额为:$(1 + 15\%)×60 = 69$(万元)
B超市今年销售额为:$(1 + 10\%)×90 = 99$(万元)
答:A超市今年“春节”期间的销售额为69万元,B超市今年“春节”期间的销售额为99万元。
根据题意,得:
$(1 + 15\%)x + (1 + 10\%)(150 - x) = 168$
解得:$x = 60$
则B超市去年销售额为:$150 - 60 = 90$(万元)
A超市今年销售额为:$(1 + 15\%)×60 = 69$(万元)
B超市今年销售额为:$(1 + 10\%)×90 = 99$(万元)
答:A超市今年“春节”期间的销售额为69万元,B超市今年“春节”期间的销售额为99万元。
3. 在长方形ABCD中放入六个相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE= x cm,依题意可列方程为(
A.16-3x= 8
B.8+2x= 16-3x
C.8+2x= 16-x
D.8+2x= x+(16-3x)
D
)A.16-3x= 8
B.8+2x= 16-3x
C.8+2x= 16-x
D.8+2x= x+(16-3x)
答案:D
解析:
设小长方形的宽AE = x cm。
由图可知,小长方形的长为(8 + 2x) cm。
又因为大长方形的长AD等于小长方形的长加上小长方形的宽,且AD = 16 - 3x + x = 16 - 2x(此处根据图形中3个小长方形的宽与大长方形长的关系推导),同时AD也等于小长方形的长,即8 + 2x = 16 - 2x,整理得8 + 2x = x + (16 - 3x)。
答案:D
由图可知,小长方形的长为(8 + 2x) cm。
又因为大长方形的长AD等于小长方形的长加上小长方形的宽,且AD = 16 - 3x + x = 16 - 2x(此处根据图形中3个小长方形的宽与大长方形长的关系推导),同时AD也等于小长方形的长,即8 + 2x = 16 - 2x,整理得8 + 2x = x + (16 - 3x)。
答案:D
4. 如图,将一张正方形纸片先剪去一个宽为6 cm的长方形①后,再从剩下的长方形纸片上剪去一个宽为8 cm的长方形②.若长方形①和②的面积恰好相等,则这张正方形纸片的面积是$
576
cm^2.$答案:576 解析:设这张正方形纸片的边长为 x cm,则长方形①的长为 x cm,宽为 6 cm;长方形②的长为$(x-6)$ cm,宽为 8 cm. 因为长方形①和②的面积恰好相等,所以$6x=8(x-6)$,解得$x=24$. 所以这张正方形纸片的边长为 24 cm. 所以这张正方形纸片的面积是$24×24=576(cm^{2})$.
解析:
解:设这张正方形纸片的边长为 $ x $ cm。
长方形①的面积为 $ 6x \, \text{cm}^2 $,长方形②的面积为 $ 8(x - 6) \, \text{cm}^2 $。
由题意得:$ 6x = 8(x - 6) $
解得:$ x = 24 $
正方形纸片的面积为 $ 24 × 24 = 576 \, \text{cm}^2 $
答案:576
长方形①的面积为 $ 6x \, \text{cm}^2 $,长方形②的面积为 $ 8(x - 6) \, \text{cm}^2 $。
由题意得:$ 6x = 8(x - 6) $
解得:$ x = 24 $
正方形纸片的面积为 $ 24 × 24 = 576 \, \text{cm}^2 $
答案:576
5. (2025·如皋期末)在数学活动课上,小华在一张长方形白纸上画出如图①所示的8个一样大小的小长方形,再把这8个小长方形剪下,无重叠地拼成如图②所示的大正方形ABCD.若中间小正方形的边长为3,则图②中大正方形ABCD的周长为______

132
.
答案:132 解析:设小长方形的长为 x,则宽为$\frac {3}{5}x$. 因为题图②中间小正方形的边长为 3,所以$2×\frac {3}{5}x-x=3$,解得$x=15$. 所以大正方形 ABCD 的周长是$4(x+2×\frac {3}{5}x)=132$.