6. 某市出租车的收费标准为起步价10元(行驶距离不超过2 km,都需付10元车费),超过2 km,每增加1 km,加收2.6元(不足1 km按1 km算).小陈乘出租车到达目的地后共支付车费49元,则小陈乘出租车可行驶的路程最远是(不考虑其他收费)(
A.15 km
B.16 km
C.17 km
D.18 km
C
)A.15 km
B.16 km
C.17 km
D.18 km
答案:C
解析:
解:设小陈乘出租车行驶的路程最远是$x$km。
因为$49>10$,所以$x>2$。
起步价覆盖2km,超出部分为$(x-2)$km,费用为$10 + 2.6(x-2)$元。
依题意列方程:$10 + 2.6(x-2)=49$
解得:$2.6(x-2)=39$
$x-2=15$
$x=17$
答案:C
因为$49>10$,所以$x>2$。
起步价覆盖2km,超出部分为$(x-2)$km,费用为$10 + 2.6(x-2)$元。
依题意列方程:$10 + 2.6(x-2)=49$
解得:$2.6(x-2)=39$
$x-2=15$
$x=17$
答案:C
7. 某市结合地方实际,决定对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
|一户居民一个月用电量的范围|电费价格/[元/(千瓦·时)]|
|不超过150千瓦·时的部分|a|
|超过150千瓦·时,但不超过300千瓦·时的部分|0.6|
|超过300千瓦·时的部分|a+0.3|
实施“阶梯电价”收费以后,该市居民陈先生家积极响应号召节约用电,10月用电100千瓦·时,缴纳电费50元.
(1)a= ______
(2)陈先生家11月用电280千瓦·时,应缴纳电费多少元?
(3)在(2)的条件下,若陈先生家12月与11月的电费相差60元,则陈先生家12月的用电量是多少?
|一户居民一个月用电量的范围|电费价格/[元/(千瓦·时)]|
|不超过150千瓦·时的部分|a|
|超过150千瓦·时,但不超过300千瓦·时的部分|0.6|
|超过300千瓦·时的部分|a+0.3|
实施“阶梯电价”收费以后,该市居民陈先生家积极响应号召节约用电,10月用电100千瓦·时,缴纳电费50元.
(1)a= ______
0.5
.(2)陈先生家11月用电280千瓦·时,应缴纳电费多少元?
因为$150<280<300$,所以应缴纳电费$0.5×150+0.6×(280-150)=153$(元)
(3)在(2)的条件下,若陈先生家12月与11月的电费相差60元,则陈先生家12月的用电量是多少?
由题意可知,陈先生家 12 月的电费为$153+60=213$(元)或$153-60=93$(元). 设陈先生家 12 月的用电量是 x 千瓦·时. 当$x=150$时,电费为$0.5×150=75$(元);当$x=300$时,电费为$0.5×150+0.6×(300-150)=165$(元). ① 当电费为 93 元时,由题意,得$75+0.6(x-150)=93$,解得$x=180$;② 当电费为 213 元时,由题意,得$165+(0.5+0.3)(x-300)=213$,解得$x=360$. 综上所述,陈先生家 12 月的用电量是 180 千瓦·时或 360 千瓦·时
答案:(1) 0.5
(2) 解:因为$150 < 280 < 300$,所以应缴纳电费为:
$0.5×150 + 0.6×(280 - 150)$
$=75 + 0.6×130$
$=75 + 78$
$=153$(元)
(3) 解:陈先生家12月的电费为$153 + 60 = 213$元或$153 - 60 = 93$元。
设12月用电量为$x$千瓦·时。
当$x = 150$时,电费$0.5×150 = 75$元;当$x = 300$时,电费$0.5×150 + 0.6×150 = 165$元。
① 当电费为93元时,$75 + 0.6(x - 150) = 93$
$0.6(x - 150) = 18$
$x - 150 = 30$
$x = 180$
② 当电费为213元时,$165 + (0.5 + 0.3)(x - 300) = 213$
$0.8(x - 300) = 48$
$x - 300 = 60$
$x = 360$
答:12月用电量是180千瓦·时或360千瓦·时。
(2) 解:因为$150 < 280 < 300$,所以应缴纳电费为:
$0.5×150 + 0.6×(280 - 150)$
$=75 + 0.6×130$
$=75 + 78$
$=153$(元)
(3) 解:陈先生家12月的电费为$153 + 60 = 213$元或$153 - 60 = 93$元。
设12月用电量为$x$千瓦·时。
当$x = 150$时,电费$0.5×150 = 75$元;当$x = 300$时,电费$0.5×150 + 0.6×150 = 165$元。
① 当电费为93元时,$75 + 0.6(x - 150) = 93$
$0.6(x - 150) = 18$
$x - 150 = 30$
$x = 180$
② 当电费为213元时,$165 + (0.5 + 0.3)(x - 300) = 213$
$0.8(x - 300) = 48$
$x - 300 = 60$
$x = 360$
答:12月用电量是180千瓦·时或360千瓦·时。
解析:
(1) 0.5
(2) 解:因为$150 < 280 < 300$,所以应缴纳电费为:
$0.5×150 + 0.6×(280 - 150)$
$=75 + 0.6×130$
$=75 + 78$
$=153$(元)
(3) 解:陈先生家12月的电费为$153 + 60 = 213$元或$153 - 60 = 93$元。
设12月用电量为$x$千瓦·时。
当$x = 150$时,电费$0.5×150 = 75$元;当$x = 300$时,电费$0.5×150 + 0.6×150 = 165$元。
① 当电费为93元时,$75 + 0.6(x - 150) = 93$
$0.6(x - 150) = 18$
$x - 150 = 30$
$x = 180$
② 当电费为213元时,$165 + (0.5 + 0.3)(x - 300) = 213$
$0.8(x - 300) = 48$
$x - 300 = 60$
$x = 360$
答:12月用电量是180千瓦·时或360千瓦·时。
(2) 解:因为$150 < 280 < 300$,所以应缴纳电费为:
$0.5×150 + 0.6×(280 - 150)$
$=75 + 0.6×130$
$=75 + 78$
$=153$(元)
(3) 解:陈先生家12月的电费为$153 + 60 = 213$元或$153 - 60 = 93$元。
设12月用电量为$x$千瓦·时。
当$x = 150$时,电费$0.5×150 = 75$元;当$x = 300$时,电费$0.5×150 + 0.6×150 = 165$元。
① 当电费为93元时,$75 + 0.6(x - 150) = 93$
$0.6(x - 150) = 18$
$x - 150 = 30$
$x = 180$
② 当电费为213元时,$165 + (0.5 + 0.3)(x - 300) = 213$
$0.8(x - 300) = 48$
$x - 300 = 60$
$x = 360$
答:12月用电量是180千瓦·时或360千瓦·时。
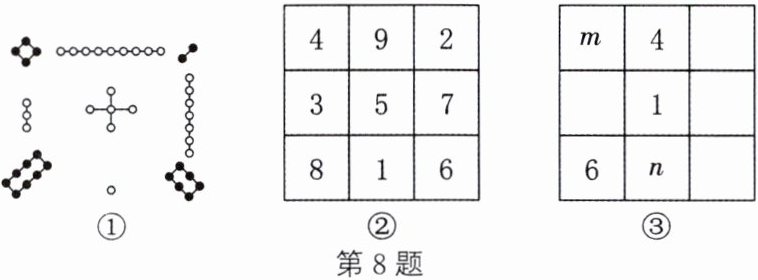
8. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”(如图①).把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方(如图②),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条斜对角线上的三个数之和都相等,就得到一个广义的三阶幻方.如图③所示的方格中填写了一些数和字母,若其能构成一个广义的三阶幻方,则n^m的值为多少?

-8
答案:设题图③中右上角的数为 x,右下角的数为 y. 由题意,可得$m+4+x=6+1+x,6+n+y=m+1+y$,解得$m=3,n=-2$. 所以$n^{m}=(-2)^{3}=-8$
解析:
设题图③中右上角的数为$x$,右下角的数为$y$。
因为幻方中每条斜对角线上的三个数之和相等,所以第一行斜对角线(从左上到右下)的和为$m + 1 + y$,第二行斜对角线(从右上到左下)的和为$6 + 1 + x$,同时第一行横向的和为$m + 4 + x$,第三列纵向的和为$x + 1 + y$(这里利用横向和斜向和相等,即$m + 4 + x = 6 + 1 + x$,可消去$x$)。
由$m + 4 + x = 6 + 1 + x$,两边同时减去$x$,得$m + 4 = 7$,解得$m = 3$。
又因为幻方中每个竖列的三个数之和相等,第三列纵向的和为$x + 1 + y$,第一列纵向的和为$m + 6$(这里原解析可能是利用另一条对角线和竖列和,即$6 + n + y = m + 1 + y$,两边同时减去$y$),由$6 + n + y = m + 1 + y$,两边同时减去$y$,得$6 + n = m + 1$,把$m = 3$代入,得$6 + n = 4$,解得$n = -2$。
所以$n^m = (-2)^3 = -8$。
答案:$-8$
因为幻方中每条斜对角线上的三个数之和相等,所以第一行斜对角线(从左上到右下)的和为$m + 1 + y$,第二行斜对角线(从右上到左下)的和为$6 + 1 + x$,同时第一行横向的和为$m + 4 + x$,第三列纵向的和为$x + 1 + y$(这里利用横向和斜向和相等,即$m + 4 + x = 6 + 1 + x$,可消去$x$)。
由$m + 4 + x = 6 + 1 + x$,两边同时减去$x$,得$m + 4 = 7$,解得$m = 3$。
又因为幻方中每个竖列的三个数之和相等,第三列纵向的和为$x + 1 + y$,第一列纵向的和为$m + 6$(这里原解析可能是利用另一条对角线和竖列和,即$6 + n + y = m + 1 + y$,两边同时减去$y$),由$6 + n + y = m + 1 + y$,两边同时减去$y$,得$6 + n = m + 1$,把$m = 3$代入,得$6 + n = 4$,解得$n = -2$。
所以$n^m = (-2)^3 = -8$。
答案:$-8$