15. 宋代数学家杨辉称“幻方”为“纵横图”,传说最早出现的幻方是夏禹时代的“洛书”,杨辉的著作《续古摘奇算法》中总结了“洛书”的构造. 在如图所示的三阶幻方中,每行、每列、每条斜对角线上的三个数之和都相等,则“”位置上的数是(
A.$4$
B.$5$
C.$6$
D.$7$
D
)A.$4$
B.$5$
C.$6$
D.$7$
答案:D
16. 已知关于$x的一元一次方程\frac{x}{2025} - a = 2025x的解是x = 5$,则关于$y的一元一次方程\frac{y + 2}{2025} - 2025y = a + 4050$的解是______
$ y = 3 $
.答案:$ y = 3 $
解析:
解:因为关于$x$的一元一次方程$\frac{x}{2025} - a = 2025x$的解是$x = 5$,
所以将$x = 5$代入方程得:$\frac{5}{2025} - a = 2025×5$,即$\frac{5}{2025} - 2025×5 = a$。
对于关于$y$的方程$\frac{y + 2}{2025} - 2025y = a + 4050$,
将$a = \frac{5}{2025} - 2025×5$代入得:
$\frac{y + 2}{2025} - 2025y = \frac{5}{2025} - 2025×5 + 4050$,
因为$4050 = 2025×2$,所以$-2025×5 + 4050 = -2025×5 + 2025×2 = -2025×3$,
方程可化为:$\frac{y + 2}{2025} - 2025y = \frac{5}{2025} - 2025×3$,
整理得:$\frac{y + 2}{2025} - \frac{5}{2025} = 2025y - 2025×3$,
即$\frac{y + 2 - 5}{2025} = 2025(y - 3)$,$\frac{y - 3}{2025} = 2025(y - 3)$,
移项得:$\frac{y - 3}{2025} - 2025(y - 3) = 0$,$(y - 3)(\frac{1}{2025} - 2025) = 0$,
因为$\frac{1}{2025} - 2025 ≠ 0$,所以$y - 3 = 0$,解得$y = 3$。
$y = 3$
所以将$x = 5$代入方程得:$\frac{5}{2025} - a = 2025×5$,即$\frac{5}{2025} - 2025×5 = a$。
对于关于$y$的方程$\frac{y + 2}{2025} - 2025y = a + 4050$,
将$a = \frac{5}{2025} - 2025×5$代入得:
$\frac{y + 2}{2025} - 2025y = \frac{5}{2025} - 2025×5 + 4050$,
因为$4050 = 2025×2$,所以$-2025×5 + 4050 = -2025×5 + 2025×2 = -2025×3$,
方程可化为:$\frac{y + 2}{2025} - 2025y = \frac{5}{2025} - 2025×3$,
整理得:$\frac{y + 2}{2025} - \frac{5}{2025} = 2025y - 2025×3$,
即$\frac{y + 2 - 5}{2025} = 2025(y - 3)$,$\frac{y - 3}{2025} = 2025(y - 3)$,
移项得:$\frac{y - 3}{2025} - 2025(y - 3) = 0$,$(y - 3)(\frac{1}{2025} - 2025) = 0$,
因为$\frac{1}{2025} - 2025 ≠ 0$,所以$y - 3 = 0$,解得$y = 3$。
$y = 3$
17. (2024·通州期末)某商店采购了一批节能灯,每盏灯$20$元. 在运输过程中损坏了$2$盏,然后以每盏$25$元的价格售完,共获利$150$元. 该商店共采购了
40
盏节能灯.答案:40
解析:
解:设该商店共采购了$x$盏节能灯。
根据题意,得$25(x - 2) - 20x = 150$
解得$x = 40$
答:该商店共采购了$40$盏节能灯。
根据题意,得$25(x - 2) - 20x = 150$
解得$x = 40$
答:该商店共采购了$40$盏节能灯。
18. 某公路一侧原有路灯$106$盏(公路两端均装有路灯),相邻两盏路灯之间的距离为$36$米. 为节约用电,现计划全部更换为新型节能灯,且相邻两盏路灯之间的距离变为$54$米,则需更换新型节能灯
71
盏.答案:71 解析:设需更换新型节能灯 $ x $ 盏,则 $ 54(x - 1) = 36×(106 - 1) $,解得 $ x = 71 $。所以需更换新型节能灯 71 盏。
解析:
解:设需更换新型节能灯 $ x $ 盏。
因为公路两端均装路灯,原有路灯106盏,相邻距离36米,所以公路总长为 $ 36×(106 - 1) $ 米。
更换后相邻距离54米,新型灯盏数为 $ x $,则公路总长也可表示为 $ 54(x - 1) $ 米。
根据公路总长不变,可得方程:
$ 54(x - 1) = 36×(106 - 1) $
解得 $ x = 71 $。
71
因为公路两端均装路灯,原有路灯106盏,相邻距离36米,所以公路总长为 $ 36×(106 - 1) $ 米。
更换后相邻距离54米,新型灯盏数为 $ x $,则公路总长也可表示为 $ 54(x - 1) $ 米。
根据公路总长不变,可得方程:
$ 54(x - 1) = 36×(106 - 1) $
解得 $ x = 71 $。
71
19. 解方程:
(1) $3(x - 2) - 4(2x + 1) = 7$;
(2) $\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$.
(1) $3(x - 2) - 4(2x + 1) = 7$;
(2) $\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$.
答案:(1) $ x = -\frac{17}{5} $ (2) $ x = 5 $
解析:
(1)解:$3(x - 2) - 4(2x + 1) = 7$
$3x - 6 - 8x - 4 = 7$
$-5x - 10 = 7$
$-5x = 17$
$x = -\frac{17}{5}$
(2)解:$\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$
$\frac{10x - 20}{2} - \frac{10x + 10}{5} = 3$
$5x - 10 - (2x + 2) = 3$
$5x - 10 - 2x - 2 = 3$
$3x - 12 = 3$
$3x = 15$
$x = 5$
$3x - 6 - 8x - 4 = 7$
$-5x - 10 = 7$
$-5x = 17$
$x = -\frac{17}{5}$
(2)解:$\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$
$\frac{10x - 20}{2} - \frac{10x + 10}{5} = 3$
$5x - 10 - (2x + 2) = 3$
$5x - 10 - 2x - 2 = 3$
$3x - 12 = 3$
$3x = 15$
$x = 5$
20. 老师在批改小刚作业时发现,小刚在解方程$\frac{x + 1}{2} - 1 = ■ + \frac{2 - x}{3}$时,把“$2 - x$”抄成了“$x - 2$”,解得$x = 5$,而且“$■$”处的数也模糊不清了.
(1) 求“$■$”处的数;
(2) 请你求出原方程正确的解.
(1) 求“$■$”处的数;
(2) 请你求出原方程正确的解.
答案:(1) 设“■”处的数为 $ a $。将 $ x = 5 $ 代入 $ \frac{x + 1}{2} - 1 = ■ + \frac{x - 2}{3} $,得 $ \frac{5 + 1}{2} - 1 = a + \frac{5 - 2}{3} $,解得 $ a = 1 $。所以“■”处的数为 1 (2) 因为“■”处的数为 1,所以原方程为 $ \frac{x + 1}{2} - 1 = 1 + \frac{2 - x}{3} $,解得 $ x = \frac{13}{5} $
解析:
(1) 设“■”处的数为 $a$。将 $x = 5$ 代入抄错后的方程 $\frac{x + 1}{2} - 1 = a + \frac{x - 2}{3}$,得 $\frac{5 + 1}{2} - 1 = a + \frac{5 - 2}{3}$,即 $3 - 1 = a + 1$,解得 $a = 1$。
(2) 由(1)知“■”处的数为 1,原方程为 $\frac{x + 1}{2} - 1 = 1 + \frac{2 - x}{3}$。去分母,得 $3(x + 1) - 6 = 6 + 2(2 - x)$,去括号,得 $3x + 3 - 6 = 6 + 4 - 2x$,移项合并同类项,得 $5x = 13$,解得 $x = \frac{13}{5}$。
(2) 由(1)知“■”处的数为 1,原方程为 $\frac{x + 1}{2} - 1 = 1 + \frac{2 - x}{3}$。去分母,得 $3(x + 1) - 6 = 6 + 2(2 - x)$,去括号,得 $3x + 3 - 6 = 6 + 4 - 2x$,移项合并同类项,得 $5x = 13$,解得 $x = \frac{13}{5}$。
21. 某种长方体包装盒的表面展开图如图所示,如果该长方体包装盒的长比宽多$4cm$,求这种长方体包装盒的体积.
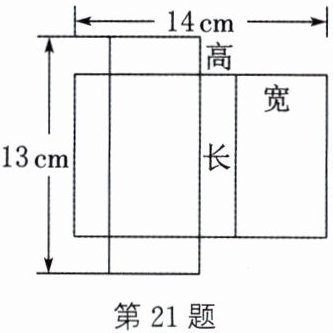

答案:设这种长方体包装盒的宽为 $ x cm $,则它的高为 $ \frac{14}{2} - x = (7 - x) cm $,长为 $ (x + 4) cm $。由题意,得 $ (x + 4) + 2(7 - x) = 13 $,解得 $ x = 5 $,则 $ 7 - x = 2 $,$ x + 4 = 9 $。所以这种长方体包装盒的长为 9 cm,宽为 5 cm,高为 2 cm,则体积为 $ 9×5×2 = 90(cm^{3}) $
解析:
设这种长方体包装盒的宽为 $ x \, \text{cm} $,则高为 $ \frac{14}{2} - x = (7 - x) \, \text{cm} $,长为 $ (x + 4) \, \text{cm} $。
由题意,得 $ (x + 4) + 2(7 - x) = 13 $。
解得 $ x = 5 $。
则高为 $ 7 - 5 = 2 \, \text{cm} $,长为 $ 5 + 4 = 9 \, \text{cm} $。
体积为 $ 9 × 5 × 2 = 90 \, \text{cm}^3 $。
答:这种长方体包装盒的体积为 $ 90 \, \text{cm}^3 $。
由题意,得 $ (x + 4) + 2(7 - x) = 13 $。
解得 $ x = 5 $。
则高为 $ 7 - 5 = 2 \, \text{cm} $,长为 $ 5 + 4 = 9 \, \text{cm} $。
体积为 $ 9 × 5 × 2 = 90 \, \text{cm}^3 $。
答:这种长方体包装盒的体积为 $ 90 \, \text{cm}^3 $。