1. (2024·辽宁)如图是由5个相同的小立方块搭成的几何体,从上面看这个几何体得到的图形是(
A
)答案:A
解析:
从上面看该几何体,底层有三个小立方块呈“L”形分布,上层右侧有一个小立方块。观察各选项,A选项符合从上面看到的图形。
A
A
2. (2024·资阳)如图所示为从前面、左面、上面看某立体图形得到的三个平面图形,则该立体图形是(
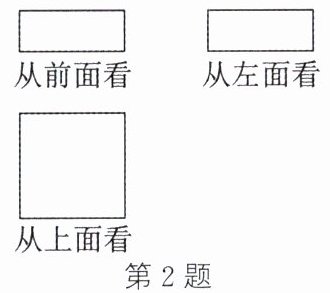
A.长方体
B.棱锥
C.圆锥
D.球体
A
)
A.长方体
B.棱锥
C.圆锥
D.球体
答案:A
解析:
从前面看是长方形,从左面看是长方形,从上面看是正方形。长方体的三视图可能是长方形和正方形,棱锥、圆锥、球体的三视图不符合此特征。
A
A
3. (2024·宿迁)将“科、技、自、立、自、强”六个字分别写在某正方体的表面上,如图是它的一种表面展开图,在原正方体中,与“强”字所在面相对的面上的汉字是(

A.自
B.立
C.科
D.技
C
)
A.自
B.立
C.科
D.技
答案:C
解析:
解:在正方体表面展开图中,相对的面之间一定相隔一个正方形。观察展开图可知,“强”与“科”中间隔一个正方形,所以“强”字所在面相对的面上的汉字是“科”。
答案:C
答案:C
4. 如图,D是线段AB的中点,延长线段AB至点C,使得BC= AB.有下列结论:①AB= 2AD;②AC= 2BC;③AD= BD= $\frac{1}{3}$AC;④BC= $\frac{1}{3}$AC;⑤BD= $\frac{1}{2}$BC;⑥AC= 4BD.其中,正确的有(

A.①③④⑥
B.①②⑤⑥
C.①②③④
D.②③⑤⑥
B
)
A.①③④⑥
B.①②⑤⑥
C.①②③④
D.②③⑤⑥
答案:B
解析:
解:设 $ AB = 2x $。
∵ D 是 AB 中点,∴ $ AD = BD = \frac{1}{2}AB = x $。
∵ $ BC = AB $,∴ $ BC = 2x $。
∴ $ AC = AB + BC = 2x + 2x = 4x $。
① $ AB = 2x $,$ 2AD = 2x $,则 $ AB = 2AD $,正确;
② $ AC = 4x $,$ 2BC = 4x $,则 $ AC = 2BC $,正确;
③ $ AD = BD = x $,$ \frac{1}{3}AC = \frac{4x}{3} $,则 $ AD = BD \neq \frac{1}{3}AC $,错误;
④ $ BC = 2x $,$ \frac{1}{3}AC = \frac{4x}{3} $,则 $ BC \neq \frac{1}{3}AC $,错误;
⑤ $ BD = x $,$ \frac{1}{2}BC = x $,则 $ BD = \frac{1}{2}BC $,正确;
⑥ $ AC = 4x $,$ 4BD = 4x $,则 $ AC = 4BD $,正确。
正确的有①②⑤⑥。
答案:B
∵ D 是 AB 中点,∴ $ AD = BD = \frac{1}{2}AB = x $。
∵ $ BC = AB $,∴ $ BC = 2x $。
∴ $ AC = AB + BC = 2x + 2x = 4x $。
① $ AB = 2x $,$ 2AD = 2x $,则 $ AB = 2AD $,正确;
② $ AC = 4x $,$ 2BC = 4x $,则 $ AC = 2BC $,正确;
③ $ AD = BD = x $,$ \frac{1}{3}AC = \frac{4x}{3} $,则 $ AD = BD \neq \frac{1}{3}AC $,错误;
④ $ BC = 2x $,$ \frac{1}{3}AC = \frac{4x}{3} $,则 $ BC \neq \frac{1}{3}AC $,错误;
⑤ $ BD = x $,$ \frac{1}{2}BC = x $,则 $ BD = \frac{1}{2}BC $,正确;
⑥ $ AC = 4x $,$ 4BD = 4x $,则 $ AC = 4BD $,正确。
正确的有①②⑤⑥。
答案:B
5. 已知线段AB= 8,在线段AB上取点C,使得AC:CB= 1:3,延长CA至点D,使得AD= 2AC,E是线段CB的中点,则线段ED的长为(
A.5
B.9
C.10
D.16
B
)A.5
B.9
C.10
D.16
答案:B
解析:
解:
∵AB=8,AC:CB=1:3,
∴AC=8×(1/(1+3))=2,CB=8×(3/(1+3))=6。
∵AD=2AC,
∴AD=2×2=4,
∵E是CB中点,
∴CE=CB/2=6/2=3。
∴ED=AD+AC+CE=4+2+3=9。
答案:B
∵AB=8,AC:CB=1:3,
∴AC=8×(1/(1+3))=2,CB=8×(3/(1+3))=6。
∵AD=2AC,
∴AD=2×2=4,
∵E是CB中点,
∴CE=CB/2=6/2=3。
∴ED=AD+AC+CE=4+2+3=9。
答案:B
6. 用棱长为1cm的小正方体搭成如图所示的几何体,则它的表面积为
22
$cm^{2}$.答案:22
解析:
解:从正面看有4个小正方形,从后面看有4个小正方形;从左面看有3个小正方形,从右面看有3个小正方形;从上面看有4个小正方形,从下面看有4个小正方形。表面积为$(4+3+4)×2=11×2=22\ \text{cm}^2$。
答案:22
答案:22
7. 如图,正方体的六个面上标着六个连续的整数.若相对的两个面上所标之数的和相等,则这六个数的和为
81
.答案:81
解析:
解:由图可知正方体面上有11、14、15,设六个连续整数为$n$,$n+1$,$n+2$,$n+3$,$n+4$,$n+5$。
情况一:若最小数为11,则六个数为11,12,13,14,15,16。其中11,14,15均在其中,符合题意。
相对面和相等,六个数之和为$11+12+13+14+15+16=81$,此时相对面和为$81÷3=27$。11与16(11+16=27),12与15(12+15=27),13与14(13+14=27),满足相对面和相等。
情况二:若最小数小于11,如10,则六个数为10,11,12,13,14,15,此时11,14,15在其中,但10,11,12,13,14,15中11与14、15可能相邻,而正方体相对面不相邻,经检验不符合相对面和相等条件。
综上,这六个数的和为81。
答案:81
情况一:若最小数为11,则六个数为11,12,13,14,15,16。其中11,14,15均在其中,符合题意。
相对面和相等,六个数之和为$11+12+13+14+15+16=81$,此时相对面和为$81÷3=27$。11与16(11+16=27),12与15(12+15=27),13与14(13+14=27),满足相对面和相等。
情况二:若最小数小于11,如10,则六个数为10,11,12,13,14,15,此时11,14,15在其中,但10,11,12,13,14,15中11与14、15可能相邻,而正方体相对面不相邻,经检验不符合相对面和相等条件。
综上,这六个数的和为81。
答案:81
8. 如图,在每个小正方形的边长都是1的3×3方格纸中,3个白色的小正方形已被剪掉,现需在编号为①~⑥的小正方形(涂色部分)中,再剪掉一个小正方形,从而使余下的5个小正方形恰好能折成一个棱长为1的无盖正方体,则需要再剪掉的小正方形可能是______(填序号).


答案:①或②或③
解析:
要使余下的5个小正方形能折成一个无盖正方体,需满足无盖正方体展开图的特征(共8种:“1-4-1”型3种,“2-3-1”型3种,“2-2-2”型1种,“3-3”型1种)。分析如下:
剪掉①:剩余小正方形为②③④⑤⑥。可构成“2-3”型展开图(②③为一列,④⑤⑥为另一列且与②③相连),能折成无盖正方体。
剪掉②:剩余小正方形为①③④⑤⑥。可构成“1-4”型展开图(①为一行,③④⑤⑥为另一行且相连),能折成无盖正方体。
剪掉③:剩余小正方形为①②④⑤⑥。可构成“2-3”型展开图(①②为一列,④⑤⑥为另一列且相连),能折成无盖正方体。
剪掉④、⑤、⑥时,剩余图形无法构成无盖正方体展开图。
需要再剪掉的小正方形可能是①或②或③。
答案:①或②或③
剪掉①:剩余小正方形为②③④⑤⑥。可构成“2-3”型展开图(②③为一列,④⑤⑥为另一列且与②③相连),能折成无盖正方体。
剪掉②:剩余小正方形为①③④⑤⑥。可构成“1-4”型展开图(①为一行,③④⑤⑥为另一行且相连),能折成无盖正方体。
剪掉③:剩余小正方形为①②④⑤⑥。可构成“2-3”型展开图(①②为一列,④⑤⑥为另一列且相连),能折成无盖正方体。
剪掉④、⑤、⑥时,剩余图形无法构成无盖正方体展开图。
需要再剪掉的小正方形可能是①或②或③。
答案:①或②或③