15. 如图,射线OA的方向是北偏东$15^{\circ }$,射线OB的方向是北偏西$40^{\circ },∠AOB= ∠AOC$,射线OD是OB的反向延长线.
(1) 射线OC的方向是
(2) 求$∠COD$的度数;
(3) 若射线OE平分$∠COD$,求$∠AOE$的度数.
(1) 射线OC的方向是
北偏东$70^{\circ}$
;(2) 求$∠COD$的度数;
因为$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$,$∠AOB=∠AOC$,所以$∠BOC=110^{\circ}$.又因为射线$OD$是$OB$的反向延长线,所以$∠BOD=180^{\circ}$.所以$∠COD=180^{\circ}-110^{\circ}=70^{\circ}$
(3) 若射线OE平分$∠COD$,求$∠AOE$的度数.
因为$∠COD=70^{\circ}$,$OE$平分$∠COD$,所以$∠COE=35^{\circ}$.因为$∠AOC=∠AOB=55^{\circ}$,所以$∠AOE=55^{\circ}+35^{\circ}=90^{\circ}$
答案:(1)北偏东$70^{\circ}$ (2)因为$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$,$∠AOB=∠AOC$,所以$∠BOC=110^{\circ}$.又因为射线$OD$是$OB$的反向延长线,所以$∠BOD=180^{\circ}$.所以$∠COD=180^{\circ}-110^{\circ}=70^{\circ}$ (3)因为$∠COD=70^{\circ}$,$OE$平分$∠COD$,所以$∠COE=35^{\circ}$.因为$∠AOC=∠AOB=55^{\circ}$,所以$∠AOE=55^{\circ}+35^{\circ}=90^{\circ}$
解析:
(1)北偏东$70^{\circ}$
(2)解:因为射线OA的方向是北偏东$15^{\circ}$,射线OB的方向是北偏西$40^{\circ}$,所以$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$。
因为$∠AOB=∠AOC$,所以$∠AOC=55^{\circ}$,则$∠BOC=∠AOB + ∠AOC=55^{\circ}+55^{\circ}=110^{\circ}$。
因为射线OD是OB的反向延长线,所以$∠BOD=180^{\circ}$。
所以$∠COD=∠BOD - ∠BOC=180^{\circ}-110^{\circ}=70^{\circ}$。
(3)解:因为$∠COD=70^{\circ}$,OE平分$∠COD$,所以$∠COE=\frac{1}{2}∠COD=\frac{1}{2}×70^{\circ}=35^{\circ}$。
因为$∠AOC=55^{\circ}$,所以$∠AOE=∠AOC + ∠COE=55^{\circ}+35^{\circ}=90^{\circ}$。
(2)解:因为射线OA的方向是北偏东$15^{\circ}$,射线OB的方向是北偏西$40^{\circ}$,所以$∠AOB=40^{\circ}+15^{\circ}=55^{\circ}$。
因为$∠AOB=∠AOC$,所以$∠AOC=55^{\circ}$,则$∠BOC=∠AOB + ∠AOC=55^{\circ}+55^{\circ}=110^{\circ}$。
因为射线OD是OB的反向延长线,所以$∠BOD=180^{\circ}$。
所以$∠COD=∠BOD - ∠BOC=180^{\circ}-110^{\circ}=70^{\circ}$。
(3)解:因为$∠COD=70^{\circ}$,OE平分$∠COD$,所以$∠COE=\frac{1}{2}∠COD=\frac{1}{2}×70^{\circ}=35^{\circ}$。
因为$∠AOC=55^{\circ}$,所以$∠AOE=∠AOC + ∠COE=55^{\circ}+35^{\circ}=90^{\circ}$。
16. 直线l上线段$AB= 6$,线段$CD= 2$(点A在点B的左侧,点C在点D的左侧).
(1) 若线段$BC= 1$,则线段AD的长为
(2) 如图①,P,Q分别为AD,BC的中点,求线段PQ的长.
(3) 如图②,若线段CD从起始位置以每秒1个单位长度的速度向右运动(起始状态下,点B与点C重合),同时,点M从点A开始以每秒2个单位长度的速度向右运动,N是线段BD的中点.若$MN= 2DN$,求线段CD运动的时间.
(1) 若线段$BC= 1$,则线段AD的长为
7或9
.(2) 如图①,P,Q分别为AD,BC的中点,求线段PQ的长.
设$BC=x$,则$AD=AB+BC+CD=8+x$.因为$P$,$Q$分别为$AD$,$BC$的中点,所以$PD=\frac{1}{2}AD=4+\frac{1}{2}x$,$CQ=\frac{1}{2}BC=\frac{1}{2}x$.所以$PQ=PD-CD-CQ=4+\frac{1}{2}x-2-\frac{1}{2}x=2$
(3) 如图②,若线段CD从起始位置以每秒1个单位长度的速度向右运动(起始状态下,点B与点C重合),同时,点M从点A开始以每秒2个单位长度的速度向右运动,N是线段BD的中点.若$MN= 2DN$,求线段CD运动的时间.
设线段$CD$运动的时间为$t$秒,则$AM=2t$,$BC=t$.所以$BM=AB-AM=6-2t$或$BM=AM-AB=2t-6$,$BD=BC+CD=t+2$.因为$N$是线段$BD$的中点,所以$DN=BN=\frac{1}{2}BD=\frac{1}{2}t+1$.因为$MN=2DN$,所以$6-2t+\frac{1}{2}t+1=2(\frac{1}{2}t+1)$或$(2t-6)-(\frac{1}{2}t+1)=2(\frac{1}{2}t+1)$,解得$t=2$或$t=18$.所以线段$CD$运动的时间为2秒或18秒
答案:(1)7或9 (2)设$BC=x$,则$AD=AB+BC+CD=8+x$.因为$P$,$Q$分别为$AD$,$BC$的中点,所以$PD=\frac{1}{2}AD=4+\frac{1}{2}x$,$CQ=\frac{1}{2}BC=\frac{1}{2}x$.所以$PQ=PD-CD-CQ=4+\frac{1}{2}x-2-\frac{1}{2}x=2$ (3)设线段$CD$运动的时间为$t$秒,则$AM=2t$,$BC=t$.所以$BM=AB-AM=6-2t$或$BM=AM-AB=2t-6$,$BD=BC+CD=t+2$.因为$N$是线段$BD$的中点,所以$DN=BN=\frac{1}{2}BD=\frac{1}{2}t+1$.因为$MN=2DN$,所以$6-2t+\frac{1}{2}t+1=2(\frac{1}{2}t+1)$或$(2t-6)-(\frac{1}{2}t+1)=2(\frac{1}{2}t+1)$,解得$t=2$或$t=18$.所以线段$CD$运动的时间为2秒或18秒
解析:
(1)7或9
(2)设$BC = x$,则$AD=AB + BC + CD=6+x+2=8+x$。
∵P,Q分别为AD,BC的中点,
∴$PD=\frac{1}{2}AD=\frac{1}{2}(8 + x)=4+\frac{1}{2}x$,$CQ=\frac{1}{2}BC=\frac{1}{2}x$。
∴$PQ=PD - CD - CQ=(4+\frac{1}{2}x)-2-\frac{1}{2}x=2$。
(3)设线段CD运动的时间为$t$秒,则$AM = 2t$,$BC=t$,$BD=BC + CD=t + 2$。
∵N是线段BD的中点,∴$DN=BN=\frac{1}{2}BD=\frac{1}{2}t + 1$。
当点M在点B左侧时,$BM=AB - AM=6 - 2t$,
∵$MN=2DN$,∴$BM + BN=2DN$,即$6-2t+\frac{1}{2}t + 1=2(\frac{1}{2}t + 1)$,
解得$t = 2$。
当点M在点B右侧时,$BM=AM - AB=2t - 6$,
∵$MN=2DN$,∴$BM - BN=2DN$,即$2t - 6-(\frac{1}{2}t + 1)=2(\frac{1}{2}t + 1)$,
解得$t = 18$。
综上,线段CD运动的时间为2秒或18秒。
(2)设$BC = x$,则$AD=AB + BC + CD=6+x+2=8+x$。
∵P,Q分别为AD,BC的中点,
∴$PD=\frac{1}{2}AD=\frac{1}{2}(8 + x)=4+\frac{1}{2}x$,$CQ=\frac{1}{2}BC=\frac{1}{2}x$。
∴$PQ=PD - CD - CQ=(4+\frac{1}{2}x)-2-\frac{1}{2}x=2$。
(3)设线段CD运动的时间为$t$秒,则$AM = 2t$,$BC=t$,$BD=BC + CD=t + 2$。
∵N是线段BD的中点,∴$DN=BN=\frac{1}{2}BD=\frac{1}{2}t + 1$。
当点M在点B左侧时,$BM=AB - AM=6 - 2t$,
∵$MN=2DN$,∴$BM + BN=2DN$,即$6-2t+\frac{1}{2}t + 1=2(\frac{1}{2}t + 1)$,
解得$t = 2$。
当点M在点B右侧时,$BM=AM - AB=2t - 6$,
∵$MN=2DN$,∴$BM - BN=2DN$,即$2t - 6-(\frac{1}{2}t + 1)=2(\frac{1}{2}t + 1)$,
解得$t = 18$。
综上,线段CD运动的时间为2秒或18秒。
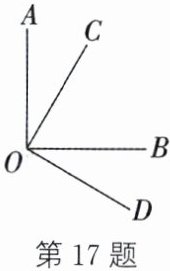
17. (2024·海安期末)如图,射线OC在$∠AOB$的内部,射线OD在$∠AOB$的外部,且$∠AOB与∠COD$互补,$∠AOC= ∠BOD$.
(1) 若$∠BOD= 30^{\circ }$,求$∠BOC$的度数;
(2) 若OB平分$∠COD$,求$∠BOC$的度数;
(3) 射线OE满足$∠COE:∠AOE= 1:2$,写出$∠COE与∠AOD$的数量关系,并说明理由.
(1) 若$∠BOD= 30^{\circ }$,求$∠BOC$的度数;
(2) 若OB平分$∠COD$,求$∠BOC$的度数;
(3) 射线OE满足$∠COE:∠AOE= 1:2$,写出$∠COE与∠AOD$的数量关系,并说明理由.

答案:因为$∠AOB$与$∠COD$互补,所以$∠AOC+∠BOC+∠BOC+∠BOD=180^{\circ}$.因为$∠AOC=∠BOD$,所以$2∠AOC+2∠BOC=180^{\circ}$.所以$∠AOC+∠BOC=90^{\circ}$,即$∠AOB=90^{\circ}$.所以$∠COD=90^{\circ}$. (1)因为$∠BOD=30^{\circ}$,所以$∠BOC=∠COD-∠BOD=60^{\circ}$ (2)因为$OB$平分$∠COD$,$∠COD=90^{\circ}$,所以$∠BOC=\frac{1}{2}∠COD=45^{\circ}$ (3)$∠AOD-∠COE=90^{\circ}$或$∠AOD-3∠COE=90^{\circ}$ 理由:如图①,当$OE$在$∠AOC$的外部时,因为$∠COE:∠AOE=1:2$,所以$∠COE=∠AOC$.因为$∠AOD=∠COD+∠AOC$,所以$∠AOD=90^{\circ}+∠COE$,即$∠AOD-∠COE=90^{\circ}$.如图②,当$OE$在$∠AOC$的内部时,因为$∠COE:∠AOE=1:2$,所以$∠AOC=3∠COE$.因为$∠AOD=∠COD+∠AOC$,所以$∠AOD=90^{\circ}+3∠COE$,即$∠AOD-3∠COE=90^{\circ}$.综上所述,$∠AOD-∠COE=90^{\circ}$或$∠AOD-3∠COE=90^{\circ}$.
解析:
解:
∵∠AOB与∠COD互补,
∴∠AOB+∠COD=180°,
∵∠AOB=∠AOC+∠BOC,∠COD=∠BOC+∠BOD,
∴∠AOC+∠BOC+∠BOC+∠BOD=180°,
∵∠AOC=∠BOD,
∴2∠AOC+2∠BOC=180°,
∴∠AOC+∠BOC=90°,即∠AOB=90°,
∴∠COD=180°-∠AOB=90°.
(1)∵∠BOD=30°,∠COD=90°,
∴∠BOC=∠COD-∠BOD=90°-30°=60°.
(2)∵OB平分∠COD,∠COD=90°,
∴∠BOC=1/2∠COD=1/2×90°=45°.
(3)∠AOD-∠COE=90°或∠AOD-3∠COE=90°.
理由:
①当OE在∠AOC外部时,
∵∠COE:∠AOE=1:2,∠AOE=∠AOC+∠COE,
∴∠COE:(∠AOC+∠COE)=1:2,
∴∠AOC=∠COE,
∵∠AOD=∠AOC+∠COD=∠AOC+90°,
∴∠AOD=∠COE+90°,即∠AOD-∠COE=90°.
②当OE在∠AOC内部时,
∵∠COE:∠AOE=1:2,∠AOC=∠AOE+∠COE,
∴∠COE:∠AOE=1:2,设∠COE=x,则∠AOE=2x,
∴∠AOC=3x,
∵∠AOD=∠AOC+∠COD=3x+90°,
∴∠AOD-3∠COE=90°.
综上,∠AOD-∠COE=90°或∠AOD-3∠COE=90°.
∵∠AOB与∠COD互补,
∴∠AOB+∠COD=180°,
∵∠AOB=∠AOC+∠BOC,∠COD=∠BOC+∠BOD,
∴∠AOC+∠BOC+∠BOC+∠BOD=180°,
∵∠AOC=∠BOD,
∴2∠AOC+2∠BOC=180°,
∴∠AOC+∠BOC=90°,即∠AOB=90°,
∴∠COD=180°-∠AOB=90°.
(1)∵∠BOD=30°,∠COD=90°,
∴∠BOC=∠COD-∠BOD=90°-30°=60°.
(2)∵OB平分∠COD,∠COD=90°,
∴∠BOC=1/2∠COD=1/2×90°=45°.
(3)∠AOD-∠COE=90°或∠AOD-3∠COE=90°.
理由:
①当OE在∠AOC外部时,
∵∠COE:∠AOE=1:2,∠AOE=∠AOC+∠COE,
∴∠COE:(∠AOC+∠COE)=1:2,
∴∠AOC=∠COE,
∵∠AOD=∠AOC+∠COD=∠AOC+90°,
∴∠AOD=∠COE+90°,即∠AOD-∠COE=90°.
②当OE在∠AOC内部时,
∵∠COE:∠AOE=1:2,∠AOC=∠AOE+∠COE,
∴∠COE:∠AOE=1:2,设∠COE=x,则∠AOE=2x,
∴∠AOC=3x,
∵∠AOD=∠AOC+∠COD=3x+90°,
∴∠AOD-3∠COE=90°.
综上,∠AOD-∠COE=90°或∠AOD-3∠COE=90°.