11. 一个角的余角比这个角的$\frac {1}{2}少30^{\circ }$,请你计算出这个角的度数.
答案:设这个角的度数为$x$,则它的余角为$90^{\circ}-x$.由题意,得$\frac{1}{2}x-(90^{\circ}-x)=30^{\circ}$,解得$x=80^{\circ}$,即这个角的度数是$80^{\circ}$
解析:
解:设这个角的度数为$x$,则它的余角为$90^{\circ}-x$。
由题意,得$\frac{1}{2}x - (90^{\circ} - x) = 30^{\circ}$
去括号:$\frac{1}{2}x - 90^{\circ} + x = 30^{\circ}$
合并同类项:$\frac{3}{2}x - 90^{\circ} = 30^{\circ}$
移项:$\frac{3}{2}x = 30^{\circ} + 90^{\circ}$
计算:$\frac{3}{2}x = 120^{\circ}$
解得:$x = 80^{\circ}$
答:这个角的度数是$80^{\circ}$
由题意,得$\frac{1}{2}x - (90^{\circ} - x) = 30^{\circ}$
去括号:$\frac{1}{2}x - 90^{\circ} + x = 30^{\circ}$
合并同类项:$\frac{3}{2}x - 90^{\circ} = 30^{\circ}$
移项:$\frac{3}{2}x = 30^{\circ} + 90^{\circ}$
计算:$\frac{3}{2}x = 120^{\circ}$
解得:$x = 80^{\circ}$
答:这个角的度数是$80^{\circ}$
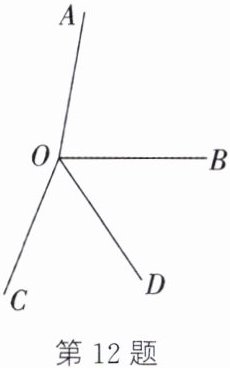
12. 如图,$∠AOB$的补角等于它的余角的10倍.
(1) 求$∠AOB$的度数;
(2) 若OD平分$∠BOC,∠AOC= 3∠BOD$,求$∠AOD$的度数.
(1) 求$∠AOB$的度数;
(2) 若OD平分$∠BOC,∠AOC= 3∠BOD$,求$∠AOD$的度数.

答案:(1)设$∠AOB=x$.由题意,得$180^{\circ}-x=10(90^{\circ}-x)$,解得$x=80^{\circ}$.所以$∠AOB$的度数为$80^{\circ}$ (2)设$∠BOD=y$,则$∠AOC=3y$.因为$OD$平分$∠BOC$,所以$∠BOC=2∠BOD=2y$.由题意,得$3y+2y+80^{\circ}=360^{\circ}$,解得$y=56^{\circ}$.所以$∠AOD=∠AOB+∠BOD=80^{\circ}+56^{\circ}=136^{\circ}$
解析:
(1)设∠AOB=x。由题意,得180°-x=10(90°-x),解得x=80°。所以∠AOB的度数为80°。
(2)设∠BOD=y,则∠AOC=3y。因为OD平分∠BOC,所以∠BOC=2∠BOD=2y。由题意,得3y+2y+80°=360°,解得y=56°。所以∠AOD=∠AOB+∠BOD=80°+56°=136°。
(2)设∠BOD=y,则∠AOC=3y。因为OD平分∠BOC,所以∠BOC=2∠BOD=2y。由题意,得3y+2y+80°=360°,解得y=56°。所以∠AOD=∠AOB+∠BOD=80°+56°=136°。
13. 如图,C为线段AB上一点,$AC= 18cm,CB= \frac {2}{3}AC$,D,E分别为线段AC,AB的中点.求DE的长.


答案:因为$AC=18\mathrm{cm}$,$CB=\frac{2}{3}AC$,所以$CB=12\mathrm{cm}$.因为$D$,$E$分别为线段$AC$,$AB$的中点,所以$AD=\frac{1}{2}AC$,$AE=\frac{1}{2}AB$.所以$DE=AE-AD=\frac{1}{2}AB-\frac{1}{2}AC=\frac{1}{2}(AB-AC)=\frac{1}{2}CB=6\mathrm{cm}$
解析:
解:因为$AC = 18\mathrm{cm}$,$CB=\frac{2}{3}AC$,所以$CB=\frac{2}{3}×18 = 12\mathrm{cm}$。
因为$D$,$E$分别为线段$AC$,$AB$的中点,所以$AD=\frac{1}{2}AC$,$AE=\frac{1}{2}AB$。
所以$DE=AE - AD=\frac{1}{2}AB-\frac{1}{2}AC=\frac{1}{2}(AB - AC)=\frac{1}{2}CB=\frac{1}{2}×12 = 6\mathrm{cm}$。
答:$DE$的长为$6\mathrm{cm}$。
因为$D$,$E$分别为线段$AC$,$AB$的中点,所以$AD=\frac{1}{2}AC$,$AE=\frac{1}{2}AB$。
所以$DE=AE - AD=\frac{1}{2}AB-\frac{1}{2}AC=\frac{1}{2}(AB - AC)=\frac{1}{2}CB=\frac{1}{2}×12 = 6\mathrm{cm}$。
答:$DE$的长为$6\mathrm{cm}$。
14. 如图,点C在线段AB上,M是AC的中点,$AB= 15,BC= 11$.
(1) 图中共有
(2) 求线段AM的长;
(3) 在线段BC上取一点N,使得$CN:NB= 5:6$,求线段MN的长.
(1) 图中共有
10
条线段;(2) 求线段AM的长;
因为点$C$在线段$AB$上,$AB=15$,$BC=11$,所以$AC=AB-BC=15-11=4$.因为$M$是$AC$的中点,所以$AM=\frac{1}{2}AC=\frac{1}{2}×4=2$
(3) 在线段BC上取一点N,使得$CN:NB= 5:6$,求线段MN的长.
因为$M$是$AC$的中点,所以$MC=\frac{1}{2}AC=2$.因为点$N$在线段$BC$上,$BC=11$,所以$CN+NB=BC=11$.又因为$CN:NB=5:6$,所以$CN=\frac{5}{5+6}BC=\frac{5}{11}×11=5$.所以$MN=MC+CN=2+5=7$
答案:(1)10 (2)因为点$C$在线段$AB$上,$AB=15$,$BC=11$,所以$AC=AB-BC=15-11=4$.因为$M$是$AC$的中点,所以$AM=\frac{1}{2}AC=\frac{1}{2}×4=2$ (3)因为$M$是$AC$的中点,所以$MC=\frac{1}{2}AC=2$.因为点$N$在线段$BC$上,$BC=11$,所以$CN+NB=BC=11$.又因为$CN:NB=5:6$,所以$CN=\frac{5}{5+6}BC=\frac{5}{11}×11=5$.所以$MN=MC+CN=2+5=7$