1. (2024·崇川期末)下列说法正确的是 (
A.$-\frac{2vt}{3}的系数是-2$
B.$3^{2}ab^{3}$的次数是6
C.$\frac{x + y}{5}$是多项式
D.$x^{2}+x - 1$的常数项为1
C
)A.$-\frac{2vt}{3}的系数是-2$
B.$3^{2}ab^{3}$的次数是6
C.$\frac{x + y}{5}$是多项式
D.$x^{2}+x - 1$的常数项为1
答案:C
解析:
A. $-\frac{2vt}{3}$的系数是$-\frac{2}{3}$,故A错误;
B. $3^{2}ab^{3}$的次数是$1 + 3 = 4$,故B错误;
C. $\frac{x + y}{5} = \frac{x}{5} + \frac{y}{5}$,是多项式,故C正确;
D. $x^{2}+x - 1$的常数项为$-1$,故D错误。
答案:C
B. $3^{2}ab^{3}$的次数是$1 + 3 = 4$,故B错误;
C. $\frac{x + y}{5} = \frac{x}{5} + \frac{y}{5}$,是多项式,故C正确;
D. $x^{2}+x - 1$的常数项为$-1$,故D错误。
答案:C
2. (1)$4x^{4}y + x^{3}y^{2}-\frac{1}{2}x^{2}y^{3}-4xy^{4}+6y^{4}$是
(2)多项式$a^{2}b-\frac{a^{3}b^{2}}{3}+5a^{3}-b^{3}$的次数最高项的系数是
五
次五
项式;(2)多项式$a^{2}b-\frac{a^{3}b^{2}}{3}+5a^{3}-b^{3}$的次数最高项的系数是
$-\frac{1}{3}$
.答案:(1) 五 五 (2) $-\frac{1}{3}$
3. (新考法·结论开放题)写出一个同时满足①只含有字母$a和b$,②每一项的次数都是2,③按字母$a$的降幂排列这些条件的二次三项式:
$a^{2}+ab+b^{2}$
.答案:答案不唯一,如 $a^{2}+ab+b^{2}$
解析:
$a^{2}+ab+b^{2}$
4. 下列计算正确的是 (
A.$-ab - ab = 0$
B.$-(3a + b)= -3a - b$
C.$5(b - 2a)= 5b - 2a$
D.$8a^{4}-6a^{2}= 2a^{2}$
B
)A.$-ab - ab = 0$
B.$-(3a + b)= -3a - b$
C.$5(b - 2a)= 5b - 2a$
D.$8a^{4}-6a^{2}= 2a^{2}$
答案:B
解析:
解:A. $-ab - ab = -2ab \neq 0$,错误;
B. $-(3a + b) = -3a - b$,正确;
C. $5(b - 2a) = 5b - 10a \neq 5b - 2a$,错误;
D. $8a^4$与$6a^2$不是同类项,不能合并,错误。
结论:B
B. $-(3a + b) = -3a - b$,正确;
C. $5(b - 2a) = 5b - 10a \neq 5b - 2a$,错误;
D. $8a^4$与$6a^2$不是同类项,不能合并,错误。
结论:B
5. 已知长方形的长为$a$,宽为$a - b(0 < b < a)$,周长为$C_{1}$,正方形的边长为$\frac{a + b}{2}$,周长为$C_{2}$,则$C_{1}-C_{2}$等于 (
A.$2a$
B.$2a - b$
C.$2a - 2b$
D.$2a - 4b$
D
)A.$2a$
B.$2a - b$
C.$2a - 2b$
D.$2a - 4b$
答案:D
解析:
解:长方形周长$C_{1}=2×[a+(a - b)]=2×(2a - b)=4a - 2b$
正方形周长$C_{2}=4×\frac{a + b}{2}=2(a + b)=2a + 2b$
$C_{1}-C_{2}=(4a - 2b)-(2a + 2b)=4a - 2b - 2a - 2b=2a - 4b$
答案:D
正方形周长$C_{2}=4×\frac{a + b}{2}=2(a + b)=2a + 2b$
$C_{1}-C_{2}=(4a - 2b)-(2a + 2b)=4a - 2b - 2a - 2b=2a - 4b$
答案:D
6. (2023·沈阳)当$a + b = 3$时,多项式$2(a + 2b)-(3a + 5b)+5$的值为
2
.答案:2
解析:
解:$2(a + 2b)-(3a + 5b)+5$
$=2a + 4b - 3a - 5b + 5$
$=-a - b + 5$
$=-(a + b) + 5$
因为$a + b = 3$,所以原式$=-3 + 5 = 2$
2
$=2a + 4b - 3a - 5b + 5$
$=-a - b + 5$
$=-(a + b) + 5$
因为$a + b = 3$,所以原式$=-3 + 5 = 2$
2
7. (2024·海门期中)若代数式$x^{2}-(3kxy + y^{2}+1)+xy - 8中不含xy$项,则$k = $
$\frac{1}{3}$
.答案:$\frac{1}{3}$
解析:
解:原式$=x^{2}-3kxy - y^{2}-1 + xy - 8$
$=x^{2}+(-3k + 1)xy - y^{2}-9$
因为代数式中不含$xy$项,所以$-3k + 1 = 0$,解得$k = \frac{1}{3}$。
$\frac{1}{3}$
$=x^{2}+(-3k + 1)xy - y^{2}-9$
因为代数式中不含$xy$项,所以$-3k + 1 = 0$,解得$k = \frac{1}{3}$。
$\frac{1}{3}$
8. 计算:
(1)$2x^{2}-4x + 7 + 5x - 8 - 3x^{2}$;
(2)$2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$.
(1)$2x^{2}-4x + 7 + 5x - 8 - 3x^{2}$;
(2)$2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$.
答案:(1) $2x^{2}-4x + 7 + 5x - 8 - 3x^{2}$
$=(2x^{2}-3x^{2}) + (-4x + 5x) + (7 - 8)$
$=-x^{2} + x - 1$
(2) $2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$
$=2y^{2} - 3x + y^{2} - 6x + 5y^{2}$
$=(2y^{2} + y^{2} + 5y^{2}) + (-3x - 6x)$
$=8y^{2} - 9x$
$=(2x^{2}-3x^{2}) + (-4x + 5x) + (7 - 8)$
$=-x^{2} + x - 1$
(2) $2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$
$=2y^{2} - 3x + y^{2} - 6x + 5y^{2}$
$=(2y^{2} + y^{2} + 5y^{2}) + (-3x - 6x)$
$=8y^{2} - 9x$
解析:
(1) $2x^{2}-4x + 7 + 5x - 8 - 3x^{2}$
$=(2x^{2}-3x^{2}) + (-4x + 5x) + (7 - 8)$
$=-x^{2} + x - 1$
(2) $2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$
$=2y^{2} - 3x + y^{2} - 6x + 5y^{2}$
$=(2y^{2} + y^{2} + 5y^{2}) + (-3x - 6x)$
$=8y^{2} - 9x$
$=(2x^{2}-3x^{2}) + (-4x + 5x) + (7 - 8)$
$=-x^{2} + x - 1$
(2) $2y^{2}-3(x-\frac{1}{3}y^{2})-(6x - 5y^{2})$
$=2y^{2} - 3x + y^{2} - 6x + 5y^{2}$
$=(2y^{2} + y^{2} + 5y^{2}) + (-3x - 6x)$
$=8y^{2} - 9x$
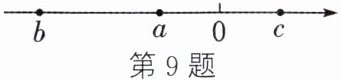
9. 有理数$a$,$b$,$c$在数轴上的对应点的位置如图所示,则化简$|a - b|-2|a - c|-|b + c|$的结果为 (
A.$a + c$
B.$a - c$
C.$2a - 2b$
D.$3a - c$
D
)
A.$a + c$
B.$a - c$
C.$2a - 2b$
D.$3a - c$
答案:D
解析:
由数轴可知:$b < a < 0 < c$,且$|b| > |a| > |c|$。
$\because b < a$,$\therefore a - b > 0$,则$|a - b| = a - b$;
$\because a < c$,$\therefore a - c < 0$,则$|a - c| = c - a$;
$\because b < 0$,$c > 0$,且$|b| > |c|$,$\therefore b + c < 0$,则$|b + c| = -b - c$。
$\therefore |a - b| - 2|a - c| - |b + c|$
$= (a - b) - 2(c - a) - (-b - c)$
$= a - b - 2c + 2a + b + c$
$= 3a - c$
答案:D
$\because b < a$,$\therefore a - b > 0$,则$|a - b| = a - b$;
$\because a < c$,$\therefore a - c < 0$,则$|a - c| = c - a$;
$\because b < 0$,$c > 0$,且$|b| > |c|$,$\therefore b + c < 0$,则$|b + c| = -b - c$。
$\therefore |a - b| - 2|a - c| - |b + c|$
$= (a - b) - 2(c - a) - (-b - c)$
$= a - b - 2c + 2a + b + c$
$= 3a - c$
答案:D