18. 现从$A$,$B$两个蔬菜市场向甲、乙两地运送蔬菜,$A$,$B$两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨. 从$A$蔬菜市场到甲地的运费为50元/吨,到乙地的运费为30元/吨;从$B$蔬菜市场到甲地的运费为60元/吨,到乙地的运费为45元/吨.
(1)设$A蔬菜市场向甲地运送蔬菜x$吨,请填写下表:
|蔬菜市场|运往甲地的质量/吨|运往乙地的质量/吨|
|A|$x$| |
|B| | |
(2)设总运费为$W$元,用含$x的式子表示W$.
(1)设$A蔬菜市场向甲地运送蔬菜x$吨,请填写下表:
|蔬菜市场|运往甲地的质量/吨|运往乙地的质量/吨|
|A|$x$| |
|B| | |
(2)设总运费为$W$元,用含$x的式子表示W$.
答案:(1) 填表如下:
|蔬菜市场|运往甲地的质量/吨|运往乙地的质量/吨|
|----|----|----|
|A|$x$|$14 - x$|
|B|$15 - x$|$x - 1$|
(2) 由题意,得 $W = 50x + 30(14 - x) + 60(15 - x) + 45(x - 1) = 5x + 1275$
|蔬菜市场|运往甲地的质量/吨|运往乙地的质量/吨|
|----|----|----|
|A|$x$|$14 - x$|
|B|$15 - x$|$x - 1$|
(2) 由题意,得 $W = 50x + 30(14 - x) + 60(15 - x) + 45(x - 1) = 5x + 1275$
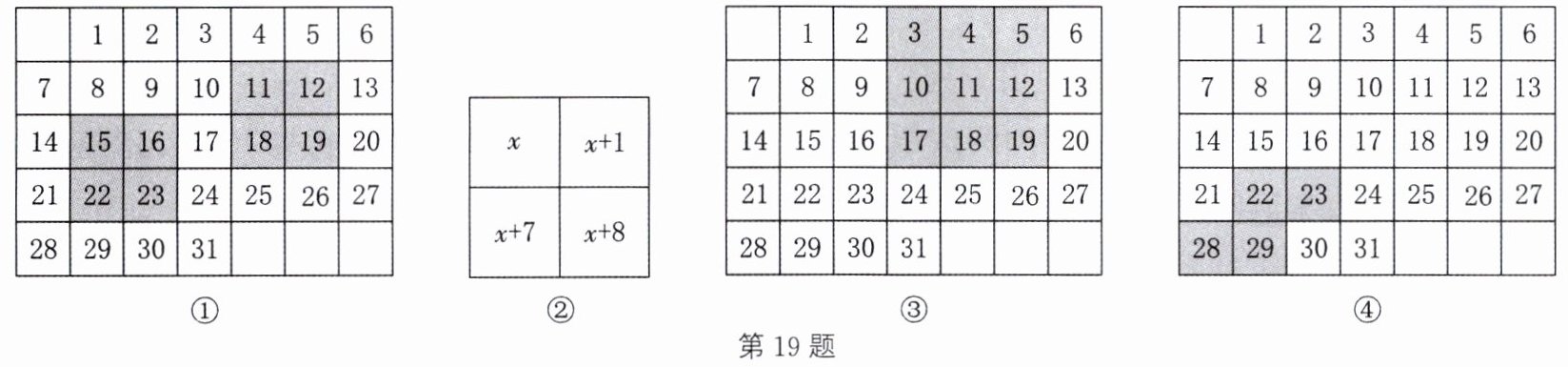
19. 如图①所示为某月的月历,涂色框中的4个数均满足“两条斜对角线上的两个数的和相等”.
探究过程:
设涂色框左上角的数为$x$,则涂色框中的4个数的表示如图②所示. 因为两条斜对角线上的两个数的和分别为$x+(x + 8)= 2x + 8$,$(x + 1)+(x + 7)= 2x + 8$,所以$x+(x + 8)= (x + 1)+(x + 7)$. 所以涂色框中的4个数均满足“两条斜对角线上的两个数的和相等”.
(1)请你根据上述的探究过程,猜测如图③所示的涂色框中的9个数的和与方框正中间的数有什么关系,并说明理由.
(2)如图④所示的涂色框中的4个数有何数量关系?请说明理由.
探究过程:
设涂色框左上角的数为$x$,则涂色框中的4个数的表示如图②所示. 因为两条斜对角线上的两个数的和分别为$x+(x + 8)= 2x + 8$,$(x + 1)+(x + 7)= 2x + 8$,所以$x+(x + 8)= (x + 1)+(x + 7)$. 所以涂色框中的4个数均满足“两条斜对角线上的两个数的和相等”.
(1)请你根据上述的探究过程,猜测如图③所示的涂色框中的9个数的和与方框正中间的数有什么关系,并说明理由.
(2)如图④所示的涂色框中的4个数有何数量关系?请说明理由.

答案:(1)9个数的和是方框正中间数的9倍。
解:设正中间的数为$x$,则9个数分别为$x - 8$,$x - 7$,$x - 6$,$x - 1$,$x$,$x + 1$,$x + 6$,$x + 7$,$x + 8$。
和为$(x - 8)+(x - 7)+(x - 6)+(x - 1)+x+(x + 1)+(x + 6)+(x + 7)+(x + 8)=9x$,故9个数的和是正中间数的9倍。
(2)两条斜对角线上的两个数的和相等。
解:设左上角的数为$x$,则4个数分别为$x$,$x + 1$,$x + 7$,$x + 8$。
斜对角线和分别为$x+(x + 8)=2x + 8$,$(x + 1)+(x + 7)=2x + 8$,故两条斜对角线上的两个数的和相等。
解:设正中间的数为$x$,则9个数分别为$x - 8$,$x - 7$,$x - 6$,$x - 1$,$x$,$x + 1$,$x + 6$,$x + 7$,$x + 8$。
和为$(x - 8)+(x - 7)+(x - 6)+(x - 1)+x+(x + 1)+(x + 6)+(x + 7)+(x + 8)=9x$,故9个数的和是正中间数的9倍。
(2)两条斜对角线上的两个数的和相等。
解:设左上角的数为$x$,则4个数分别为$x$,$x + 1$,$x + 7$,$x + 8$。
斜对角线和分别为$x+(x + 8)=2x + 8$,$(x + 1)+(x + 7)=2x + 8$,故两条斜对角线上的两个数的和相等。