23. (10分)如图,用三种不同的正方形和一个缺角的长方形(图形AFHGNE)拼成一个大长方形$A B C D$,其中$G H= a, G N= 3, B F= b$,设长方形$A B C D的周长为L$.
(1)用含$a, b的代数式表示L= $______;
(2)若$P= 3 a^{2}+2 b^{2}-5 a-8 b+1$,当$a= \frac{1}{3}, b= \frac{1}{2}$时,求$3 P+2 L$的值.
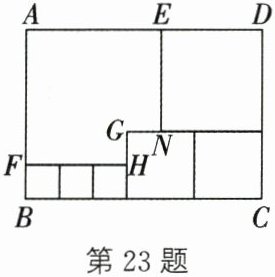
(1)用含$a, b的代数式表示L= $______;
(2)若$P= 3 a^{2}+2 b^{2}-5 a-8 b+1$,当$a= \frac{1}{3}, b= \frac{1}{2}$时,求$3 P+2 L$的值.

答案:
(1) 10a + 16b - 6 解析:如图,因为易知 CM = GH + FB = a + b,所以 DM = NM = 2(a + b) - 3 = 2a + 2b - 3,AD = BC = 3b + 2(a + b) = 2a + 5b。所以 CD = DM + CM = 2a + 2b - 3 + a + b = 3a + 3b - 3。所以长方形 ABCD 的周长 L = 2(AD + CD) = 2(2a + 5b + 3a + 3b - 3) = 10a + 16b - 6。
(2) 因为 P = 3a² + 2b² - 5a - 8b + 1,L = 10a + 16b - 6,所以 3P + 2L = 3(3a² + 2b² - 5a - 8b + 1) + 2(10a + 16b - 6) = 9a² + 6b² - 15a - 24b + 3 + 20a + 32b - 12 = 9a² + 6b² + 5a + 8b - 9。当 a = $\frac{1}{3}$,b = $\frac{1}{2}$ 时,3P + 2L = 9×($\frac{1}{3}$)² + 6×($\frac{1}{2}$)² + 5×$\frac{1}{3}$ + 8×$\frac{1}{2}$ - 9 = 1 + $\frac{3}{2}$ + $\frac{5}{3}$ + 4 - 9 = -$\frac{5}{6}$
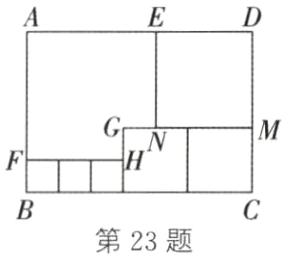
(1) 10a + 16b - 6 解析:如图,因为易知 CM = GH + FB = a + b,所以 DM = NM = 2(a + b) - 3 = 2a + 2b - 3,AD = BC = 3b + 2(a + b) = 2a + 5b。所以 CD = DM + CM = 2a + 2b - 3 + a + b = 3a + 3b - 3。所以长方形 ABCD 的周长 L = 2(AD + CD) = 2(2a + 5b + 3a + 3b - 3) = 10a + 16b - 6。
(2) 因为 P = 3a² + 2b² - 5a - 8b + 1,L = 10a + 16b - 6,所以 3P + 2L = 3(3a² + 2b² - 5a - 8b + 1) + 2(10a + 16b - 6) = 9a² + 6b² - 15a - 24b + 3 + 20a + 32b - 12 = 9a² + 6b² + 5a + 8b - 9。当 a = $\frac{1}{3}$,b = $\frac{1}{2}$ 时,3P + 2L = 9×($\frac{1}{3}$)² + 6×($\frac{1}{2}$)² + 5×$\frac{1}{3}$ + 8×$\frac{1}{2}$ - 9 = 1 + $\frac{3}{2}$ + $\frac{5}{3}$ + 4 - 9 = -$\frac{5}{6}$
