1. 相反数的意义:
(1) 代数意义:只有
(2) 几何意义:在数轴上位于
2. 相反数的表示:一般地,一个数 $ a $ 的相反数可表示为
3. 相反数的求法:求一个数的相反数,只要在它前面添上
4. 多重符号的化简规律:多重符号化简的结果由
(1) 代数意义:只有
符号
不同的两个数互为相反数. 特别地,0 的相反数是0
.(2) 几何意义:在数轴上位于
原点
两侧,并且到原点距离相等
的两个点所表示的两个数互为相反数.2. 相反数的表示:一般地,一个数 $ a $ 的相反数可表示为
$-a$
.3. 相反数的求法:求一个数的相反数,只要在它前面添上
$-$
号即可.4. 多重符号的化简规律:多重符号化简的结果由
$-$
号的个数决定,与$+$
号的个数无关. 如果$-$
号的个数是奇数,那么结果为负
;如果$-$
号的个数是偶数,那么结果为正
.答案:1. (1) 符号 0 (2) 原点 相等 2. $-a$ 3. $-$ 4. $-$ $+$ $-$ 负 $-$ 正
1. (2023·青岛) $ \frac{1}{7} $ 的相反数是 (
A.$ -\frac{1}{7} $
B.$ \frac{1}{7} $
C.$ -7 $
D.$ 7 $
A
)A.$ -\frac{1}{7} $
B.$ \frac{1}{7} $
C.$ -7 $
D.$ 7 $
答案:A
解析:
根据相反数的定义,只有符号不同的两个数互为相反数。
$\frac{1}{7}$的相反数是$-\frac{1}{7}$。
答案:A
$\frac{1}{7}$的相反数是$-\frac{1}{7}$。
答案:A
2. 化简 $ -(-\frac{5}{7}) $ 的结果是 (
A.$ -\frac{7}{5} $
B.$ \frac{7}{5} $
C.$ -\frac{5}{7} $
D.$ \frac{5}{7} $
D
)A.$ -\frac{7}{5} $
B.$ \frac{7}{5} $
C.$ -\frac{5}{7} $
D.$ \frac{5}{7} $
答案:D
解析:
解:$-(-\frac{5}{7})=\frac{5}{7}$
答案:D
答案:D
3. 填空:
(1) $ -1.6 $ 与
(2) $ -\frac{1}{3} $ 是
(3)
(1) $ -1.6 $ 与
1.6
互为相反数;(2) $ -\frac{1}{3} $ 是
$\frac{1}{3}$
的相反数;(3)
$-0.5$
的相反数是 $ 0.5 $.答案:(1) 1.6 (2) $\frac{1}{3}$ (3) $-0.5$
4. 如果点 $ A $,$ B $,$ C $,$ D $ 在数轴上的位置如图所示,那么 $ -3 $ 的相反数所对应的点是

A
.
答案:A
解析:
解:-3的相反数是3,由图可知数轴上表示3的点是A。
答案:A
答案:A
5. 给出下列各数:$ 4 $,$ -\frac{1}{2} $,$ -(-\frac{2}{3}) $,$ +(-4.5) $,$ 0 $,$ -(+3) $. 请写出它们的相反数,并把所有的数(包括相反数)在数轴上表示出来.
答案:
4 的相反数是 $-4$;$-\frac{1}{2}$ 的相反数是 $\frac{1}{2}$;$-(-\frac{2}{3})$ 的相反数是 $-\frac{2}{3}$;$+(-4.5)$ 的相反数是 4.5;0 的相反数是 0;$-(+3)$ 的相反数是 3 在数轴上表示如图所示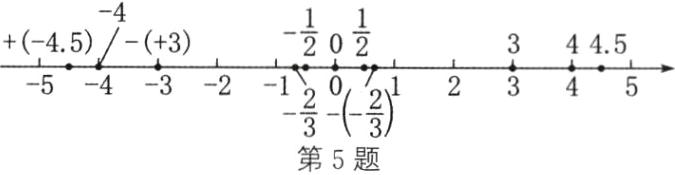
4 的相反数是 $-4$;$-\frac{1}{2}$ 的相反数是 $\frac{1}{2}$;$-(-\frac{2}{3})$ 的相反数是 $-\frac{2}{3}$;$+(-4.5)$ 的相反数是 4.5;0 的相反数是 0;$-(+3)$ 的相反数是 3 在数轴上表示如图所示
