1. 尺规作图:用
无刻度的
直尺和圆规
作图.答案:无刻度的 圆规
2. 线段的基本事实:两点的所有连线中,
线段
最短.简单说成:两点之间,线段最短
.答案:线段 线段最短
3. 连接两点的线段的
长度
,叫作这两点间的距离.答案:长度
4. 线段的中点:
(1) 概念:若线段上的一点把线段分成
(2) 符号语言:如图,因为C是线段AB的中点,所以
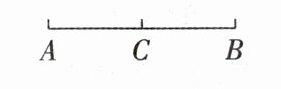
(1) 概念:若线段上的一点把线段分成
相等
的两条线段,则这个点叫作线段的中点.(2) 符号语言:如图,因为C是线段AB的中点,所以
$ AC = BC = \frac{1}{2}AB $ (或 $ AB = 2AC = 2BC $)
.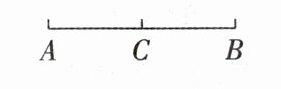
答案:(1) 相等 (2) $ AC = BC = \frac{1}{2}AB $ (或 $ AB = 2AC = 2BC $)
1. 如图,$AB= CD$,则AC与BD的大小关系是 (
A.$AC>BD$
B.$AC<BD$
C.$AC= BD$
D.无法确定
C
)A.$AC>BD$
B.$AC<BD$
C.$AC= BD$
D.无法确定
答案:C
解析:
由图可知,点的顺序为A、B、C、D在同一直线上。
因为$AC = AB + BC$,$BD = BC + CD$,又已知$AB = CD$,所以$AC = BD$。
C
因为$AC = AB + BC$,$BD = BC + CD$,又已知$AB = CD$,所以$AC = BD$。
C
2. 已知C是线段AB上一点,下列不能确定C是AB中点的条件是 (
A.$AC= BC$
B.$AC= \frac{1}{2}AB$
C.$AB= 2BC$
D.$AC+CB= AB$
D
)A.$AC= BC$
B.$AC= \frac{1}{2}AB$
C.$AB= 2BC$
D.$AC+CB= AB$
答案:D
解析:
解:A. 若$AC = BC$,且$C$在线段$AB$上,则$C$是$AB$中点;
B. 若$AC=\frac{1}{2}AB$,且$C$在线段$AB$上,则$C$是$AB$中点;
C. 若$AB = 2BC$,且$C$在线段$AB$上,则$C$是$AB$中点;
D. 无论$C$在线段$AB$上何处,均有$AC + CB=AB$,不能确定$C$是中点。
答案:D
B. 若$AC=\frac{1}{2}AB$,且$C$在线段$AB$上,则$C$是$AB$中点;
C. 若$AB = 2BC$,且$C$在线段$AB$上,则$C$是$AB$中点;
D. 无论$C$在线段$AB$上何处,均有$AC + CB=AB$,不能确定$C$是中点。
答案:D
3. 已知线段$AB= 8cm$,点C在直线AB上,$BC= 3cm$,则线段AC的长为
5 cm 或 11 cm
.答案:5 cm 或 11 cm
解析:
解:当点C在线段AB上时,AC=AB-BC=8-3=5cm;
当点C在线段AB的延长线上时,AC=AB+BC=8+3=11cm。
线段AC的长为5cm或11cm。
当点C在线段AB的延长线上时,AC=AB+BC=8+3=11cm。
线段AC的长为5cm或11cm。
4. 如图,点C在线段AB上,$BC= 2AC$,D是线段AB的中点.如果$AC= 4$,那么BD的长为
6
.答案:6
解析:
解:因为 $AC = 4$,$BC = 2AC$,所以 $BC = 2×4 = 8$。
所以 $AB = AC + BC = 4 + 8 = 12$。
因为 D 是线段 AB 的中点,所以 $BD = \frac{1}{2}AB = \frac{1}{2}×12 = 6$。
6
所以 $AB = AC + BC = 4 + 8 = 12$。
因为 D 是线段 AB 的中点,所以 $BD = \frac{1}{2}AB = \frac{1}{2}×12 = 6$。
6
5. 如图,M,N是线段AB的三等分点,C是NB的中点.若$AB= 10cm$,求CM的长.


答案:因为 M,N 是线段 AB 的三等分点,所以 $ AM = MN = BN $,$ AB = 3BN $。因为 C 是 NB 的中点,所以 $ BN = 2CN $。因为 $ AB = 10 cm $,所以 $ BN = MN = \frac{10}{3} cm $。所以 $ CN = \frac{5}{3} cm $。所以 $ CM = MN + CN = \frac{10}{3} + \frac{5}{3} = 5(cm) $
解析:
解:因为M,N是线段AB的三等分点,
所以$AM=MN=BN$,$AB=3BN$。
因为$AB=10cm$,
所以$BN=MN=\frac{10}{3}cm$。
因为C是NB的中点,
所以$CN=\frac{1}{2}BN=\frac{1}{2}×\frac{10}{3}=\frac{5}{3}cm$。
所以$CM=MN+CN=\frac{10}{3}+\frac{5}{3}=5cm$。
答:CM的长为5cm。
所以$AM=MN=BN$,$AB=3BN$。
因为$AB=10cm$,
所以$BN=MN=\frac{10}{3}cm$。
因为C是NB的中点,
所以$CN=\frac{1}{2}BN=\frac{1}{2}×\frac{10}{3}=\frac{5}{3}cm$。
所以$CM=MN+CN=\frac{10}{3}+\frac{5}{3}=5cm$。
答:CM的长为5cm。