例2 王老师买了一些课外书送给小朋友,第一次送了总本数的一半,第二次又送了剩下本数的一半,这时还剩4本课外书。这些课外书一共有多少本?
思路分析 从最后还剩4本课外书开始往前推算,借助图示更容易理解,如下图。
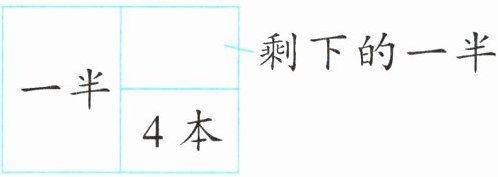
由图可知,剩下的一半也是4本,说明第一次送完后剩下的就是2个4本,即8本,那么总数的一半是8本,说明总数就是2个8本,用乘法计算。
规范解答 4×2= 8(本)
8×2= 16(本)
答:这些课外书一共有16本。
思路分析 从最后还剩4本课外书开始往前推算,借助图示更容易理解,如下图。
由图可知,剩下的一半也是4本,说明第一次送完后剩下的就是2个4本,即8本,那么总数的一半是8本,说明总数就是2个8本,用乘法计算。
规范解答 4×2= 8(本)
8×2= 16(本)
答:这些课外书一共有16本。
答案：解析：本题主要考查了通过逆向推理和乘法运算来解决实际问题。通过从最后剩余的书本数量出发，逐步推算出最初的总数。
答案：
剩下的一半是4本，
那么第一次送完后剩下：
$4 × 2 = 8$（本），
总数的一半是8本，
那么总数为：
$8 × 2 = 16$（本）。
答：这些课外书一共有16本。
答案：
剩下的一半是4本，
那么第一次送完后剩下：
$4 × 2 = 8$（本），
总数的一半是8本，
那么总数为：
$8 × 2 = 16$（本）。
答：这些课外书一共有16本。
跟踪练习3 小雅、小兰和小艾三人用一些纸折纸鹤。小雅用了一半的纸后,小兰又用了剩下的纸的一半,小艾用了最后剩下的7张。三人一共用了多少张纸?
答案：7×4=28（张）
解析：
解：小艾用之前剩下的纸：7张
小兰用之前剩下的纸：7×2=14（张）
小雅用之前的纸（总纸数）：14×2=28（张）
答：三人一共用了28张纸。
小兰用之前剩下的纸：7×2=14（张）
小雅用之前的纸（总纸数）：14×2=28（张）
答：三人一共用了28张纸。
例3 (2025·淮安洪泽区期末改编)把一根长36米的绳子对折两次后,沿折痕剪开,每段长多少米?
思路分析 生活中有时会把一根绳子进行对折,甚至对折后接着对折若干次。在这样的对折中,存在的规律是每对折一次后,绳子的长度就会被除以2,对折几次后绳子的长度就会被连续除以几个2;反过来,已知对折几次后的绳长,要求原绳长就要用对折后的绳长连续乘几个2。题目中提到对折两次,对折后成了2×2= 4(段)。
规范解答 2×2= 4(段)
36÷4= 9(米)
答:每段长9米。
思路分析 生活中有时会把一根绳子进行对折,甚至对折后接着对折若干次。在这样的对折中,存在的规律是每对折一次后,绳子的长度就会被除以2,对折几次后绳子的长度就会被连续除以几个2;反过来,已知对折几次后的绳长,要求原绳长就要用对折后的绳长连续乘几个2。题目中提到对折两次,对折后成了2×2= 4(段)。
规范解答 2×2= 4(段)
36÷4= 9(米)
答:每段长9米。
答案：解析：
本题考查的是利用除法解决实际问题。
绳子被对折两次，每次对折都会使绳子的段数翻倍。
因此，对折两次后，绳子被分成了 $2 × 2 = 4$ 段。
原绳子长36米，对折两次后，每段的长度就是总长度除以段数，即 $36 ÷ 4 = 9(米)$。
答案：
2×2= 4(段)，
36÷4= 9(米)，
答：每段长9米。
本题考查的是利用除法解决实际问题。
绳子被对折两次，每次对折都会使绳子的段数翻倍。
因此，对折两次后，绳子被分成了 $2 × 2 = 4$ 段。
原绳子长36米，对折两次后，每段的长度就是总长度除以段数，即 $36 ÷ 4 = 9(米)$。
答案：
2×2= 4(段)，
36÷4= 9(米)，
答：每段长9米。