10.请用一副三角板拼出75°的角,尽可能多地写出不同的拼法.
答案：方法有:
(1)30°+45°;
(2)60°+(45°−30°);
(3)90°−(45°−30°)等
(1)30°+45°;
(2)60°+(45°−30°);
(3)90°−(45°−30°)等
11.中考新考法 操作探究 一张长方形纸片,用剪刀剪去一个角,还剩几个角？请动手试一试,有几种剪法,并画出来.
答案：
如图，还剩5个角或4个角或3个角，共3种.
如图，还剩5个角或4个角或3个角，共3种.
12.分类讨论思想 中考新考法 归纳一般结论 已知$\angle AOB= \alpha$,$\angle COD= \beta$,保持$\angle AOB$不动,$\angle COD$的OC边与OA边重合,然后将$\angle COD$绕点O按顺时针方向任意转动一个角度$\gamma(0^\circ\leq\gamma\leq360^\circ)$.(本题中研究的其他角的度数均小于180°)
[特例分析]
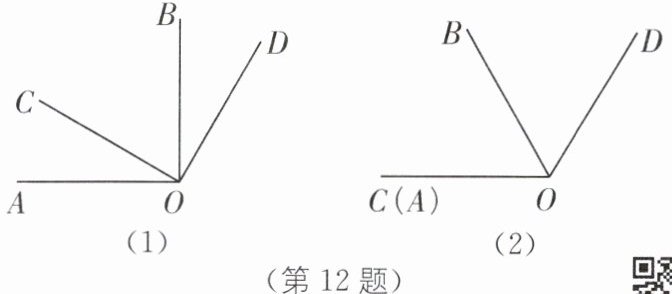
(1)如图(1),若$\gamma=30^\circ$,$\alpha=\beta=90^\circ$,则$\angle BOD= $ °,$\angle AOD + \angle BOC= $ °.
[一般化研究]
(2)如图(2),若$\alpha + \beta=180^\circ$,随着$\gamma$的变化,探索$\angle AOD与\angle BOC$的数量关系,并说明理由.
[继续一般化]
(3)随着$\gamma$的变化,直接写出$\angle AOD与\angle BOC$的数量关系(结果用含$\alpha$,$\beta$的代数式表示).
[特例分析]
(1)如图(1),若$\gamma=30^\circ$,$\alpha=\beta=90^\circ$,则$\angle BOD= $ °,$\angle AOD + \angle BOC= $ °.
[一般化研究]
(2)如图(2),若$\alpha + \beta=180^\circ$,随着$\gamma$的变化,探索$\angle AOD与\angle BOC$的数量关系,并说明理由.
[继续一般化]
(3)随着$\gamma$的变化,直接写出$\angle AOD与\angle BOC$的数量关系(结果用含$\alpha$,$\beta$的代数式表示).
答案：
(1)30 180 [解析]由转动角γ=30°,α=β=90°可知，∠BOD=30°.
∵α=β=90°，即∠AOB=∠COD=90°，
∴∠AOD+∠BOC=(∠AOC+∠COD)+(∠AOB−∠AOC)=180°.
(2)∠AOD+∠BOC=180°.理由如下:如图
(1)，当OC在∠AOB内部，OD在∠AOB外部时，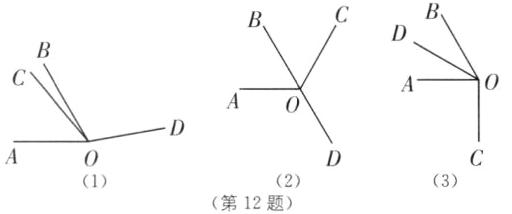
∵∠AOD=∠AOB+∠BOD，
∴∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°;如图
(2)，当OC在∠AOB外部，OD在∠AOB外部时，∠AOD+∠BOC=360°−(∠AOB+∠COD)=180°;如图
(3)，当OC在∠AOB外部，OD在∠AOB内部时，
∵∠AOD=∠AOB−∠BOD，
∴∠AOD+∠BOC=∠AOB−∠BOD+∠BOC=∠AOB+∠COD=180°.综上所述，∠AOD+∠BOC=180°.
(3)当A,0,D三点共线时，γ=180°−β或360°−β，当B,O,C三点共线时，γ=α或α+180°.①如图
(4)，当0≤γ＜α时，∠AOC=γ，则∠AOD=β+γ，∠BOC=α−γ，
∴∠AOD+∠BOC=α+β;
②如图
(5)，当α≤γ＜180°−β时，∠AOD=β+γ，∠BOC=γ−α，
∴∠AOD−∠BOC=α+β;③如图
(6)，当180°−β≤γ＜α+180°时，∠AOD=360°−β−γ，∠BOC=γ−α，
∴∠AOD+∠BOC=360°−α−β;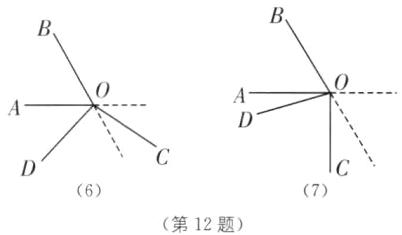
④如图
(7)，当α+180°≤γ＜360°−β时，∠AOD=360°−β−γ，∠BOC=360°−(γ−α)=360°−γ+α，
∴∠BOC−∠AOD=α+β;⑤如图
(8)，当360°−β≤γ≤360°时,∠AOD=γ−180°−(180°−β)=γ+β−360°，∠BOC=360°−γ+α，
∴∠AOD+∠BOC=α+β.
综上所述，当0≤γ＜α或360°−β≤γ＜360°时，∠AOD+∠BOC=α+β;当α≤γ＜180°−β时，∠AOD−∠BOC=α+β;当180°−β≤γ＜α+180°时，∠AOD+∠BOC=360°−α−β;当α+180°≤γ＜360°−β时，∠BOC−∠AOD=α+β.归纳总结 本题考查了角的有关计算，根据题目要求作出图形，利用角度的和差关系计算是解题的关键。
(1)30 180 [解析]由转动角γ=30°,α=β=90°可知，∠BOD=30°.
∵α=β=90°，即∠AOB=∠COD=90°，
∴∠AOD+∠BOC=(∠AOC+∠COD)+(∠AOB−∠AOC)=180°.
(2)∠AOD+∠BOC=180°.理由如下:如图
(1)，当OC在∠AOB内部，OD在∠AOB外部时，
∵∠AOD=∠AOB+∠BOD，
∴∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°;如图
(2)，当OC在∠AOB外部，OD在∠AOB外部时，∠AOD+∠BOC=360°−(∠AOB+∠COD)=180°;如图
(3)，当OC在∠AOB外部，OD在∠AOB内部时，
∵∠AOD=∠AOB−∠BOD，
∴∠AOD+∠BOC=∠AOB−∠BOD+∠BOC=∠AOB+∠COD=180°.综上所述，∠AOD+∠BOC=180°.
(3)当A,0,D三点共线时，γ=180°−β或360°−β，当B,O,C三点共线时，γ=α或α+180°.①如图
(4)，当0≤γ＜α时，∠AOC=γ，则∠AOD=β+γ，∠BOC=α−γ，
∴∠AOD+∠BOC=α+β;
②如图(5)，当α≤γ＜180°−β时，∠AOD=β+γ，∠BOC=γ−α，
∴∠AOD−∠BOC=α+β;③如图
(6)，当180°−β≤γ＜α+180°时，∠AOD=360°−β−γ，∠BOC=γ−α，
∴∠AOD+∠BOC=360°−α−β;
④如图(7)，当α+180°≤γ＜360°−β时，∠AOD=360°−β−γ，∠BOC=360°−(γ−α)=360°−γ+α，
∴∠BOC−∠AOD=α+β;⑤如图
(8)，当360°−β≤γ≤360°时,∠AOD=γ−180°−(180°−β)=γ+β−360°，∠BOC=360°−γ+α，
∴∠AOD+∠BOC=α+β.
综上所述，当0≤γ＜α或360°−β≤γ＜360°时，∠AOD+∠BOC=α+β;当α≤γ＜180°−β时，∠AOD−∠BOC=α+β;当180°−β≤γ＜α+180°时，∠AOD+∠BOC=360°−α−β;当α+180°≤γ＜360°−β时，∠BOC−∠AOD=α+β.归纳总结 本题考查了角的有关计算，根据题目要求作出图形，利用角度的和差关系计算是解题的关键。