变式2.1 如图,因为OD是∠AOC的平分线,所以$∠COD= \frac{1}{2}∠AOC.$因为OE是∠BOC的平分线,所以$∠COE= \frac{1}{2}$
∠BOC
.所以∠DOE= ∠COD+∠COE
$= \frac{1}{2}(∠AOC+∠BOC)= \frac{1}{2}∠AOB=$90
°.答案:∠BOC ∠COE 90
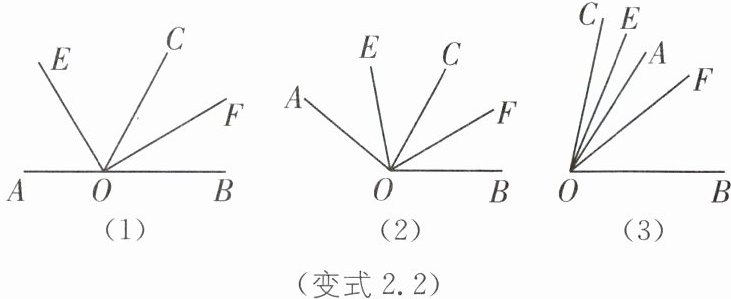
变式2.2 (2025·四川绵阳梓潼期末)如图,已知OE平分∠AOC,OF平分∠BOC.
(1)如图(1),若点A,O,B在一条直线上,则∠EOF=
(2)如图(2),若点A,O,B不在一条直线上,∠AOB= 140°,则∠EOF=
(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB有何数量关系?写出来并说明理由.
∠EOF=$\frac{1}{2}$∠AOB.理由如下:
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC,
∴∠EOF=∠COF + ∠COE=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB.
(1)如图(1),若点A,O,B在一条直线上,则∠EOF=
90°
.(2)如图(2),若点A,O,B不在一条直线上,∠AOB= 140°,则∠EOF=
70°
.(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB有何数量关系?写出来并说明理由.

∠EOF=$\frac{1}{2}$∠AOB.理由如下:
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC,
∴∠EOF=∠COF + ∠COE=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB.
答案:
(1)90° [解析]
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC.
又∠AOB=180°,
∴∠EOF=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC + ∠AOC)=$\frac{1}{2}$∠AOB=90°.
(2)70° [解析]
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC.
又∠AOB=140°,
∴∠EOF=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC + ∠AOC)=$\frac{1}{2}$∠AOB=70°.
(3)∠EOF=$\frac{1}{2}$∠AOB.理由如下:
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC,
∴∠EOF=∠COF + ∠COE=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB.
(1)90° [解析]
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC.
又∠AOB=180°,
∴∠EOF=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC + ∠AOC)=$\frac{1}{2}$∠AOB=90°.
(2)70° [解析]
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC.
又∠AOB=140°,
∴∠EOF=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC + ∠AOC)=$\frac{1}{2}$∠AOB=70°.
(3)∠EOF=$\frac{1}{2}$∠AOB.理由如下:
∵OE 平分∠AOC,OF 平分∠BOC,
∴∠COF=$\frac{1}{2}$∠COB,∠COE=$\frac{1}{2}$∠AOC,
∴∠EOF=∠COF + ∠COE=$\frac{1}{2}$∠COB + $\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB.
3.我们已学习了角平分线的概念,那么你会用它们解决有关问题吗?
(1)如图(1)所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在A′处,BC为折痕.若∠ABC= 54°,求∠A′BD的度数;
(2)在(1)条件下,如果又将它的另一个角也斜折过去,并使BD边与BA′重合,折痕为BE,如图(2)所示,求∠CBE的度数.

(1)如图(1)所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在A′处,BC为折痕.若∠ABC= 54°,求∠A′BD的度数;
(2)在(1)条件下,如果又将它的另一个角也斜折过去,并使BD边与BA′重合,折痕为BE,如图(2)所示,求∠CBE的度数.

答案:
(1)
∵∠ABC=54°,
∴∠A'BC=∠ABC=54°,
由折叠的性质可得
∴∠A'BD=180° - ∠ABC - ∠A'BC=180° - 54° - 54°=72°.
(2)由
(1)的结论可得∠DBD'=72°,
∴∠2=$\frac{1}{2}$∠DBD'=$\frac{1}{2}$×72°=36°.
∵∠1=∠ABC=54°,
∴∠CBE=∠1 + ∠2=90°.
(1)
∵∠ABC=54°,
∴∠A'BC=∠ABC=54°,
由折叠的性质可得
∴∠A'BD=180° - ∠ABC - ∠A'BC=180° - 54° - 54°=72°.
(2)由
(1)的结论可得∠DBD'=72°,
∴∠2=$\frac{1}{2}$∠DBD'=$\frac{1}{2}$×72°=36°.
∵∠1=∠ABC=54°,
∴∠CBE=∠1 + ∠2=90°.
变式3.1 (2025·贵州遵义绥阳区期末)如图,长方形ABCD沿直线EF,EG折叠后,点A和点D分别落在直线l上的点A′和点D′处,若∠2= 60°,则∠1的度数为(

A.30°
B.50°
C.55°
D.60°
A
).
A.30°
B.50°
C.55°
D.60°
答案:A [解析]由折叠知∠D'EG=∠2=60°,
∠AEF=∠1.又∠D'EG + ∠2 + ∠AEF + ∠1=180°,
∴∠1=$\frac{1}{2}$(180° - ∠D'EG - ∠2)=$\frac{1}{2}$×(180° - 60° - 60°)=30°.故选 A.
∠AEF=∠1.又∠D'EG + ∠2 + ∠AEF + ∠1=180°,
∴∠1=$\frac{1}{2}$(180° - ∠D'EG - ∠2)=$\frac{1}{2}$×(180° - 60° - 60°)=30°.故选 A.